CBSE 10th Standard Maths Subject Polynomials Case Study Questions 2021
By QB365 on 21 May, 2021
QB365 Provides the updated CASE Study Questions for Class 10 Maths, and also provide the detail solution for each and every case study questions . Case study questions are latest updated question pattern from NCERT, QB365 will helps to get more marks in Exams
QB365 - Question Bank Software
CBSE 10th Standard Maths Subject Polynomials Case Study Questions 2021
10th Standard CBSE
-
Reg.No. :
Maths
-
While playing in garden, Sahiba saw a honeycomb and asked her mother what is that. She replied that it's a honeycomb made by honey bees to store honey. Also, she told her that the shape of the honeycomb formed is parabolic. The mathematical representation of the honeycomb structure is shown in the graph.
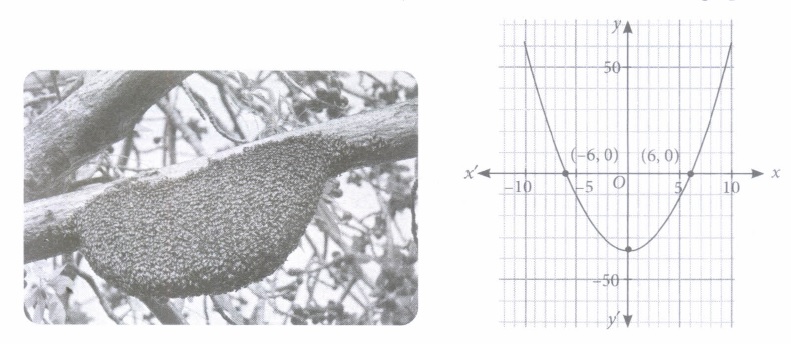
Based on the above information, answer the following questions.
(i) Graph of a quadratic polynomial is in___________shape.(a) straight line (b) parabolic (c) circular (d) None of these (ii) The expression of the polynomial represented by the graph is
(a) x2-49 (b) x2-64 (c) x2-36 (d) x2-81 (iii) Find the value of the polynomial represented by the graph when x = 6.
(a) -2 (b) -1 (c) 0 (d) 1 (iv) The sum of zeroes of the polynomial x2 + 2x - 3 is
(a) -1 (b) -2 (c) 2 (d) 1 (v) If the sum of zeroes of polynomial at2 + 5t + 3a is equal to their product, then find the value of a.
(a) -5 (b) -3 \(\text { (c) } \frac{5}{3}\) \(\text { (d) } \frac{-5}{3}\) (a) -
Just before the morning assembly a teacher of kindergarten school observes some clouds in the sky and so she cancels the assembly. She also observes that the clouds has a shape of the polynomial. The mathematical representation of a cloud is shown in the figure.

(i) Find the zeroes of the polynomial represented by the graph.(a) -1/2,7/2 (b) 1/2, -7/2 (c) -1/2, -7/2 (d) 1/2,7/2 (ii) What will be the expression for the polynomial represented by the graph?
\((a) p(x)=12 x^{2}-4 x-7\) \((b) p(x)=-x^{2}-12 x+3\) \((c) p(x)=4 x^{2}+12 x+7\) \((d) p(x)=-4 x^{2}-12 x+7\) (iii) What will be the value of polynomial represented by the graph, when x = 3?
(a) 65 (b) -65 (c) 68 (d) -68 (iv) If a and \(\beta\) are the zeroes of the polynomial \(f(x)=x^{2}+2 x-8 \text { , then } \alpha^{4}+\beta^{4}=\)
(a) 262 (b) 252 (c) 272 (d) 282 (v) Find a quadratic polynomial where sum and product of its zeroes are 0,\(\sqrt (7)\) respectively.
\((a) k\left(x^{2}+\sqrt{7}\right)\) \((b) k\left(x^{2}-\sqrt{7}\right)\) \((c) k\left(x^{2}+\sqrt{5}\right)\) (d) none of these (a) -
Pankaj's father gave him some money to buy avocado from the market at the rate of p(x) = x2 - 24x + 128. Let a , \(\beta\) are the zeroes of p(x).
Based on the above information, answer the following questions.

(i) Find the value of a and \(\beta\), where a < \(\beta\).(a) -8, -16 (b) 8,16 (c) 8,15 (d) 4,9 (ii) Find the value of \(\alpha\) + \(\beta\) + \(\alpha\)\(\beta\).
(a) 151 (b) 158 (c) 152 (d) 155 (iii) The value of p(2) is
(a) 80 (b) 81 (c) 83 (d) 84 (iv) If \(\alpha\) and \(\beta\) are zeroes of \(x^{2}+x-2, \text { then } \frac{1}{\alpha}+\frac{1}{\beta}=\)
(a) 1/2 (b) 1/3 (c) 1/4 (d) 1/5 (v) If sum of zeroes of \(q(x)=k x^{2}+2 x+3 k\) is equal to their product, then k =
(a) 2/3 (b) 1/3 (c) -2/3 (d) -1/3 (a) -
Two friends Trisha and Rohan during their summer vacations went to Manali. They decided to go for trekking. While trekking they observes that the trekking path is in the shape of a parabola. The mathematical representation of the track is shown in the graph.

Based on the above information, answer the following questions.
(i) The zeroes of the polynomial whose graph is given, are(a) 4,7 (b) -4,7 (c) 4,3 (d) 7,10 (ii) What will be the expression of the given polynomial p(x)?
\((a) x^{2}-3 x+\mathbf{3} 8\) \((b) -x^{2}+4 x+28\) \((c) x^{2}-4 x+28\) \((d) -x^{2}+3 x+28\) (iii) Product of zeroes of the given polynomial is
(a) -28 (b) 28 (c) -30 (d) 30 (iv) The zeroes of the polynomial 9x2 - 5 are
\((a) \frac{3}{\sqrt{5}}, \frac{-3}{\sqrt{5}}\) \((b) \frac{2}{\sqrt{5}}, \frac{-2}{\sqrt{5}}\) \((c) \frac{\sqrt{5}}{3}, \frac{-\sqrt{5}}{3}\) \((d) \frac{\sqrt{5}}{2}, \frac{-\sqrt{5}}{2}\) (v) If f(x) = x2 - 13x + 1, then f(4) =
(a) 35 (b) -35 (c) 36 (d) -36 (a) -
Neeru saw a creeper on the boundary of her aunt's house which was in the shape as shown in the figure. Answer the following questions by considering that creeper has same mathematical shape as shown in the figure. Based on the above information, answer the following questions.
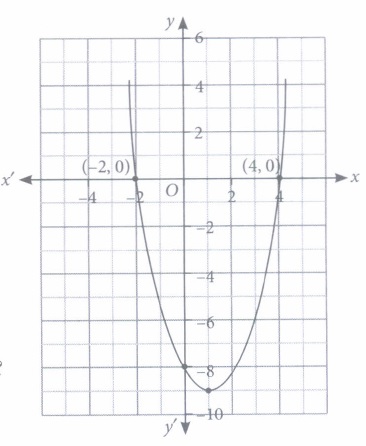
(i) The shape represents a _______ polynomial.(a) Linear (b) Cubic (c) Quadratic (d) None of these (ii) How many zeroes does the polynomial (shape of the creeper) have?
(a) 0 (b) 1 (c) 2 (d) 3 (iii) The zeroes of the polynomial, represented by the graph, are
(a) 4, -2 (b) -4,2 (c) 4,2 (d) -5,6 (iv) The expression of the polynomial, represented by the graph, is
\((a) x^{2}+2 x-8\) \((b) x^{2}-2 x-8\) \((c) x^{3}-x+8\) \((d) x^{3}-x^{2}+2 x+8\) (v) For what value of x, the value of the polynomial, represented by the graph, is -5?
(a) x=3 (b) x=-1 (c) Both (a) and (b) (d) Can't be determined (a)
Case Study Questions
*****************************************
CBSE 10th Standard Maths Subject Polynomials Case Study Questions 2021 Answer Keys
-
(i) (b): Graph of a quadratic polynomial is a parabolic in shape.
(ii) (c): Since the graph of the polynomial cuts the
x-axis at (-6,0) and (6, 0). So, the zeroes of polynomial are -6 and 6.
\(\therefore\) Required polynomial is p(x) = x2 - (-6 + 6)x + (-6)(6) = x2 - 36
(iii) (c) : We have, p(x) = x2 - 36
Now, p( 6) = 62 - 36 = 36 - 36 = 0
(iv) (b): Letf (x) = x2 + 2x - 3. Then,
\(\text { Sum of zeroes }=-\frac{\text { coefficient of } x}{\text { coefficient of } x^{2}}=-\frac{(2)}{1}=-2\)
(v) (d): The given polynomial is at2+ 5t + 3a Given, sum of zeroes = product of zeroes.
\(\Rightarrow \quad \frac{-5}{a}=\frac{3 a}{a} \Rightarrow a=\frac{-5}{3}\) -
(i) (b): Since the graph of the polynomial intersect the x-axis at \(x=\frac{1}{2}, \frac{-7}{2}\), therefore required zeroes of the polynomial are \(\frac{1}{2} \text { and } \frac{-7}{2}\)
(ii) (d): \(\because \frac{1}{2} \text { and } \frac{-7}{2}\) are the zeroes of the polynomial.
So, at \(x=\frac{1}{2}, \frac{-7}{2}\) the value of the polynomial will be 0.
From options, required polynomial is
p(x) = -4x2 - 12x + 7
(iii) (b) : we have, \(p(x)=-4 x^{2}-12 x+7\)
\(\therefore \quad p(3)=-4(3)^{2}-12(3)+7=-36-36+7=-65 \)
(iv) (c): Here \(f(x)=x^{2}+2 x-8 \text { and } \alpha, \beta \text { are its zeroes. }\)
\(\therefore \quad \alpha+\beta=-2 \text { and } \alpha \beta=-8 \)
\(\text { Now, } \alpha^{4}+\beta^{4}=\left(\alpha^{2}+\beta^{2}\right)^{2}-2 \alpha^{2} \beta^{2} \)
\(=\left((\alpha+\beta)^{2}-2 \alpha \beta\right)^{2}-2(\alpha \beta)^{2} \)
\(=\left[(-2)^{2}-2(-8)\right]^{2}-2(-8)^{2} \)
\(=[4+16]^{2}-2(-8)^{2}=(20)^{2}-2(64) \)
\(=400-128=272\)
(v) (a): We have sum of zeroes = 0 and product of zeroes = \(\sqrt(7)\)
So, required polynomial .\(=k\left(x^{2}-0 \cdot x+\sqrt{7}\right) \)
\(=k\left(x^{2}+\sqrt{7}\right)\) -
(i) (b): Given, a and \(\beta\) are the zeroes of
\(p(x)=x^{2}-24 x+128\)
\(\text { Putting } p(x)=0 \text { , we get }\)
\( x^{2}-8 x-16 x+128=0 \)
\(\Rightarrow x(x-8)-16(x-8)=0 \)
\(\Rightarrow (x-8)(x-16)=0 \Rightarrow x=8 \text { or } x=16 \)
\(\therefore \alpha=8, \beta=16\)
(ii) (c) : \(\alpha+\beta+\alpha \beta =8+16+(8)(16) =24+128=152 \)
(iii) (d) : \(p(2)=2^{2}-2 4(2)+128=4-48+128=84\)
(iv) (a): Since a and \(\beta\) are zeroes of \(x^{2}+x-2\)
\(\therefore \quad \alpha+\beta=-1 \text { and } \alpha \beta=-2 \)
\(\text { Now, } \frac{1}{\alpha}+\frac{1}{\beta}=\frac{\beta+\alpha}{\alpha \beta}=\frac{-1}{-2}=\frac{1}{2}\)
(v) (c): Sum of zeroes \(=\frac{-2}{k}\)
Product of zeroes \(=\frac{3 k}{k}=3\)
According to question, we have \(\frac{-2}{k}=3\)
\(\Rightarrow \quad k=\frac{-2}{3}\) -
(i) (b): Since, the graph intersects the x-axis at two points, namely x = -4, 7
So, -4, 7 are the zeroes of the polynomial.
(ii) (d): p(x) = -x2 + 3x + 28
(iii) (a) : \(\text { Product of zeroes }=\frac{\text { Constant term }}{\text { Coefficient of } x^{2}}\)
\(\therefore \quad \text { Required product of zeroes }=\frac{28}{-1}=-28\)
(iv) (c): We have \(9 x^{2}-5 =(3 x)^{2}-(\sqrt{5})^{2} =(3 x-\sqrt{5})(3 x+\sqrt{5}) \)
\(\therefore x=\frac{\sqrt{5}}{3} \text { or } \frac{-\sqrt{5}}{3}\)
(v) (b): Here, \(f(x)=x^{2}-13 x+1\)
\(\therefore \quad f(4)=4^{2}-13(4)+1=16-52+1=-35\) -
(i) (c) :The shape represents a quadratic polynomial.
(ii) (c): Since, the graph of polynomial cuts the x-axis at (-2, 0) and (4, 0). So, the polynomial has 2 zeroes.
(iii) (a) : The zeroes of the polynomial are -2 and 4.
(iv) (b): Required polynomial is \(p(x)=x^{2}-(-2+4) x+(-2)(4)=x^{2}-2 x-8\)
(v) (c): Consider, p(x) = -5
\(\Rightarrow \quad x^{2}-2 x-8=-5 \Rightarrow x^{2}-2 x-3=0\)
\(\Rightarrow(x-3)(x+1)=0 \Rightarrow x=-1 \text { or } x=3\)
\(\text { So, at } x=3 \text { and at } x=-1, p(x)=-5 \text { . }\)
Case Study Questions

























