CBSE 10th Standard Maths Subject Triangles Case Study Questions With Solution 2021
By QB365 on 22 May, 2021
QB365 Provides the updated CASE Study Questions for Class 10 Maths, and also provide the detail solution for each and every case study questions . Case study questions are latest updated question pattern from NCERT, QB365 will helps to get more marks in Exams
QB365 - Question Bank Software
CBSE 10th Standard Maths Subject Triangles Case Study Questions With Solution 2021
10th Standard CBSE
-
Reg.No. :
Maths
-
An aeroplane leaves an airport and flies due north at a speed of 1200km /hr. At the same time, another aeroplane leaves the same station and flies due west at the speed of 1500 km/hr as shown below. After \(1 \frac{1}{2}\) hr both the aeroplanes reaches at point P and Q respectively.
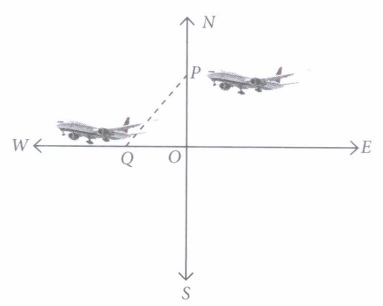
(i) Distance travelled by aeroplane towards north after \(1 \frac{1}{2}\) hr is(a) 1800 km (b) 1500 km (c) 1400km (d) 1350 km (ii) Distance travelled by aeroplane towards west after \(1 \frac{1}{2}\) hr is
(a) 1600 km (b) 1800 km (c) 2250km (d) 2400 km (iii) In the given figure,\(\angle\)POQ is
(a) 70° (b) 90° (c) 80° (d) 100° (iv) Distance between aeroplanes after \(1 \frac{1}{2}\) hr is
\((a) 450 \sqrt{41} \mathrm{~km}\) \((b) 350 \sqrt{31} \mathrm{~km}\) \((c) 125 \sqrt{12} \mathrm{~km}\) \((d) 472 \sqrt{41} \mathrm{~km}\) (v) Area of \(\Delta\)POQ is
(a) 185000km2 (b) 179000km2 (c) 186000km2 (d) 2025000 km2 (a) -
Meenal was trying to find the height of tower near his house. She is using the properties of similar triangles. The height of Meenal's house is 20 m. When Meenal's house casts a shadow of 10m long on the ground, at the same time, tower casts a shadow of 50 m long and Arun's house casts a shadow of 20 m long on the ground as shown below.
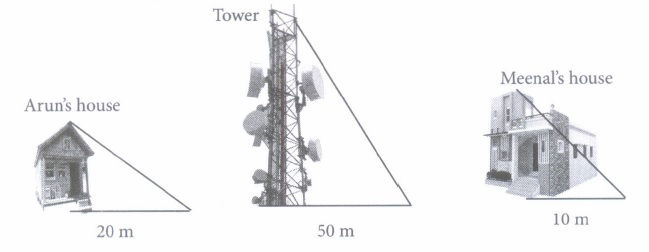
Based on the above information, answer the following questions.
(i) What is the height of tower?(a) 100 m (b) 50 m (c) 15 m (d) 45 m (ii) What will be the length of shadow of tower when Meenal's house casts a shadow of 15 m?
(a) 45 m (b) 70 m (c) 75 m (d) 72 m (iii) Height of Aruns house is
(a) 80 m (b) 75 m (c) 60 m (d) 40 m (iv) If tower casts a shadow of 40 rn, then find the length of shadow of Arun's house
(a) 18 m (b) 17 m (c) 16 m (d) 14 m (v) If tower casts a shadow of 40 m, then what will be the length of shadow of Meenal's house?
(a) 7 m (b) 9 m (c) 4 m (d) 8 m (a) -
Minister of a state went to city Q from city P. There is a route via city R such that PR \(\perp\)RQ. PR = 2x km and RQ = 2(x + 7) km. He noticed that there is a proposal to construct a 26 km highway which directly connects the two cities P and Q.
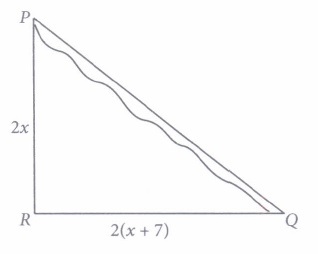
Based on the above information, answer the following questions.
(i) Which concept can be used to get the value of x?(a) Thales theorem (b) Pythagoras theorem (c) Converse ofthales theorem (d) Converse of Pythagoras theorem (ii) The value of x is
(a) 4 (b) 6 (c) 5 (d) 8 (iii) The value of PR is
(a) 10 km (b) 20 km (c) 15 km (d) 25 km (iv) The value of RQ is
(a) 12 km (b) 24 km (c) 16 km (d) 20 km (v) How much distance will be saved in reaching city Q after the construction of highway?
(a) 10 km (b) 9 km (c) 4 km (d) 8 km (a) -
Class teacher draw the shape of quadrilateral on board. Ankit observed the shape and explored on his notebook in different ways as shown below.
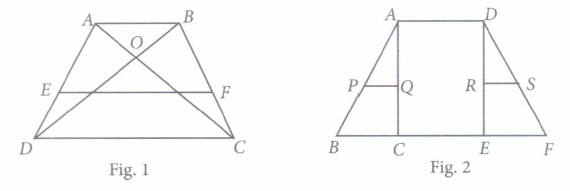
Based on the above information, answer the following questions.
(i) In if ABCD is a trapezium with AB || CD, E and F are points on non-parallel sides AD and BC respectively such that EF || AB, then \(\frac{A E}{E D}=\)(a) \(\frac{B E}{C D}\) (b) \(\frac{A B}{C D}\) (c) \(\frac{B F}{F C}\) (d) None of these (ii) In if AB || CD, and DO = 3x - 19, OB = x - 5, OC = x - 3 and AO = 3, then the value of x can be
(a) 5 or 8 (b) 8 or 9 (c) 10 or 12 (d) 13 or 14 (iii) In if OD = 3x - 1, OB = 5x - 3, OC = 2x + 1 and AO = 6x - 5, then the value of x is
(a) 0 (b) 1 (c) 2 (d) 3 (iv) In \(\Delta\) ABC, if PQ || BC and AP = 2.4 cm, AQ = 2 cm, QC = 3 cm and BC = 6 cm, then AB + PQ is equal to
(a) 7.2 cm (b) 5.9 cm (c) 2.6 cm (d) 8.4 cm (v) In \(\Delta\)DEF, if RS || EF, DR = 4x - 3, DS = 8x - 7, ER = 3x - 1 and FS = 5x - 3, then the value of x is
(a) 1 (b) 5.9 cm (c) 2.6 cm (d) 8.4 cm (a) -
Two hotels are at the ground level on either side of a mountain. On moving a certain distance towards the top of the mountain two huts are situated as shown in the figure. The ratio between the distance from hotel B to hut-2 and that ofhut-2 to mountain top is 3: 7.
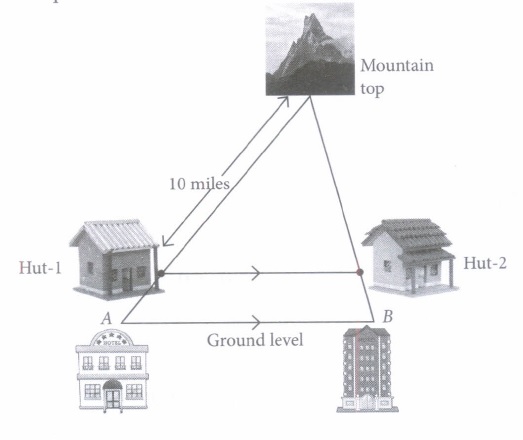
Based on the above information, answer the following questions.
(i) What is the ratio of the perimeters of the triangle formed by both hotels and mountain top to the triangle formed by both huts and mountain top?(a) 5: 2 (b) 10: 7 (c) 7: 3 (d) 3: 10 (ii) The distance between the hotel A and hut-I is
(a) 2.5 miles (b) 29 miles (c) 4.29 miles (d) 1.5 miles (iii) If the horizontal distance between the hut -1 and hut -2 is 8 miles, then the distance between the two hotels is
(a) 2.4 miles (b) 11.43 miles (c) 9 miles (d) 7 miles (iv) If the distance from mountain top to hut-1 is 5 miles more than that of distance from hotel B to mountain top, then what is the distance between hut-2 and mountain top?
(a) 3.5 miles (b) 6 miles (c) 5.5 miles (d) 4 miles (v) What is the ratio of areas of two parts formed in the complete figure?
(a) 53: 21 (b) 10: 41 (c) 51: 33 (d) 49:51 (a)
Case Study Questions
*****************************************
CBSE 10th Standard Maths Subject Triangles Case Study Questions With Solution 2021 Answer Keys
-
(i) (a): Speed = 1200 km/hr
\(\text { Time }=1 \frac{1}{2} \mathrm{hr}=\frac{3}{2} \mathrm{hr}\)
\(\therefore\) Required distance = Speed x Time
\(=1200 \times \frac{3}{2}=1800 \mathrm{~km}\)
(ii) (c): Speed = 1500 km/hr
Time = \(\frac{3}{2}\) hr.
\(\therefore\) Required distance = Speed x Time
\(=1500 \times \frac{3}{2}=2250 \mathrm{~km}\)
(iii) (b): Clearly, directions are always perpendicular to each other.
\(\therefore \quad \angle P O Q=90^{\circ}\)
(iv) (a): Distance between aeroplanes after \(1\frac{1}{2}\) hour
\(\begin{array}{l} =\sqrt{(1800)^{2}+(2250)^{2}}=\sqrt{3240000+5062500} \\ =\sqrt{8302500}=450 \sqrt{41} \mathrm{~km} \end{array}\)
(v) (d): Area of \(\Delta\)POQ= \(\frac{1}{2}\)x base x height
\(=\frac{1}{2} \times 2250 \times 1800=2250 \times 900=2025000 \mathrm{~km}^{2}\) -
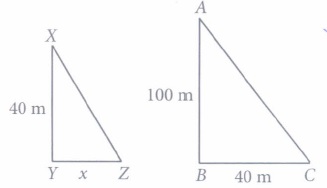
(i) (a): Since \(\Delta\)ABC - \(\Delta\)PQR
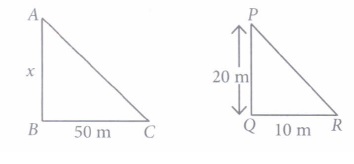
\(\therefore \quad \frac{A B}{P Q}=\frac{B C}{Q R} \Rightarrow \frac{x}{20}=\frac{50}{10} \Rightarrow x=100\)
Thus, height of tower is 100 m.
(ii) (c): Since \(\Delta\)ABC - \(\Delta\)PQR
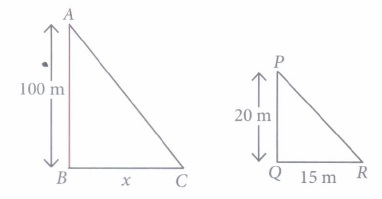
\(\therefore \quad \frac{100}{20}=\frac{x}{15} \Rightarrow x=\frac{1500}{20}=75 \mathrm{~m}\)
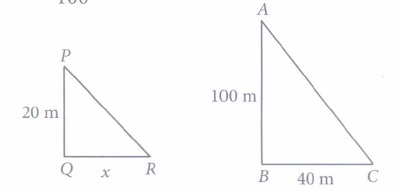
(iii) (d): Since, the shapes are similar
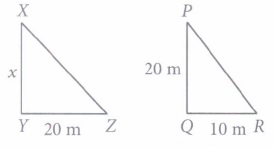
\(\therefore \quad \frac{x}{20}=\frac{20}{10} \)
\(\Rightarrow \quad x=\frac{20 \times 20}{10}=40 \mathrm{~m}\)
(iv) (b): Since, the shapes are similar, so, \(\frac{40}{100}=\frac{x}{40}\)
\(\Rightarrow\) x = 16m
(v) (d): Since, the shapes are similar, so \(\frac{20}{100}=\frac{x}{40}\)
\(\Rightarrow \quad x=\frac{20 \times 40}{100}=8 \mathrm{~m}\)
-
(i) (b)
(ii) (c): Using Pythagoras theorem, we have PQ2 = PR2 + RQ2
\(\Rightarrow(26)^{2}=(2 x)^{2}+(2(x+7))^{2} \Rightarrow 676=4 x^{2}+4(x+7)^{2} \)
\(\Rightarrow 169=x^{2}+x^{2}+49+14 x \Rightarrow x^{2}+7 x-60=0\)
\(\Rightarrow x^{2}+12 x-5 x-60=0 \)
\(\Rightarrow x(x+12)-5(x+12)=0 \Rightarrow(x-5)(x+12)=0 \)
\(\Rightarrow x=5, x=-12\)
\(\therefore \quad x=5\) [Since length can't be negative]
(iii) (a) : PR = 2x = 2 x 5 = 10 km
(iv) (b): RQ= 2(x + 7) = 2(5 + 7) = 24 km
(v) (d): Since, PR + RQ = 10 + 24 = 34 km Saved distance = 34 - 26 = 8 km -
(i) (c)
(ii) (b): Since \(\Delta\)AOB ~ \(\Delta\)COD [ByAA similarity criterion]
\(\therefore \frac{A O}{O C}=\frac{B O}{O D} \Rightarrow \frac{3}{x-3}=\frac{x-5}{3 x-19}\)
\(\Rightarrow 3(3 x-19)=(x-5)(x-3) \)
\(\Rightarrow 9 x-57=x^{2}-3 x-5 x+15 \Rightarrow x^{2}-17 x+72=0 \)
\(\Rightarrow(x-8)(x-9)=0 \Rightarrow x=8 \text { or } 9\)
(iii) (c) : Since, \(\Delta\)AOB ~ \(\Delta\)COD [ByAA similarity criterion]
\(\therefore \frac{A O}{O C}=\frac{B O}{O D} \Rightarrow \frac{6 x-5}{2 x+1}=\frac{5 x-3}{3 x-1}\)
\(\Rightarrow(6 x-5)(3 x=1)=(5 x-3)(2 x+1) \)
\(\Rightarrow \quad 18 x^{2}-6 x-15 x+5=10 x^{2}+5 x-6 x-3 \)
\(\Rightarrow \quad 8 x^{2}-20 x+8=0 \Rightarrow 2 x^{2}-5 x+2=0\)
From options, x = 2 is the only value that satisfies this equation.
(iv) (d): Since, \(\Delta\)APQ ~ \(\Delta\)ABC [ByAA similarity criterion]
\(\therefore \quad \frac{A P^{\circ}}{A B}=\frac{A Q}{A C}=\frac{P Q}{B C} \Rightarrow \frac{2.4}{A B}=\frac{2}{5}=\frac{P Q}{6} \)
\(\therefore \quad A B=\frac{2.4 \times 5}{2}=6 \mathrm{~cm} \text { and } P Q=\frac{2 \times 6}{5}=2.4 \mathrm{~cm} \)
\(\therefore \quad A B+P Q=6+2.4=8.4 \mathrm{~cm}\)
(v) (a): Since, \(\Delta\)DRS ~ \(\Delta\)DEF [ByAA similarity criterion]
\(\therefore \quad \frac{D E}{D R}=\frac{D F}{D S} \Rightarrow \frac{D E}{D R}-1=\frac{D F}{D S}-1 \)
\(\Rightarrow \frac{D E-D R}{D R}=\frac{D F-D S}{D S} \Rightarrow \frac{E R}{D R}=\frac{F S}{D S} \)
\(\Rightarrow \quad \frac{D R}{E R}=\frac{D S}{F S} \Rightarrow \frac{4 x-3}{3 x-1}=\frac{8 x-7}{5 x-3} \)
\(\Rightarrow \quad 20 x^{2}-12 x-15 x+9=24 x^{2}-8 x-21 x+7 \)
\(\Rightarrow \quad 4 x^{2}-2 x-2=0 \Rightarrow 2 x^{2}-x-1=0\)
Only option (a) i.e., x = 1 satisfies this equation. -
(i) (b): Let \(\Delta\)ABC is the triangle formed by both hotels and mountain top. \(\Delta\)CDE is the triangle formed by both huts and mountain top. Clearly, DE || AB and so
\(\triangle A B C \sim \triangle D E C\) [By AA-similarity criterion]
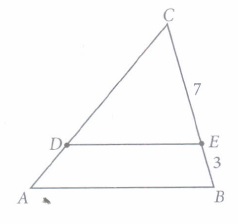
Now, required ratio = Ratio of their corresponding sides \(=\frac{B C}{E C}=\frac{10}{7}\) i.e., 10:7.
(ii) (c): Since, DE || AB, therefore
\(\frac{C D}{A D}=\frac{C E}{E B} \Rightarrow \frac{10}{A D}=\frac{7}{3} \Rightarrow A D=\frac{10 \times 3}{7}=4.29 \text { miles }\)
(iii) (b) : Since, \(\triangle A B C \sim \triangle D E C\)
\(\therefore \quad \frac{B C}{E C}=\frac{A B}{D E}\) [ \(\because\) Corresponding sides of similar triangles are proportional]
\(\Rightarrow \frac{10}{7}=\frac{A B}{8} \Rightarrow A B=\frac{80}{7}=11.43 \text { miles }\)
(iv) (a) Given, DC= 5+ BC.
Clearly, BC = 10-5 = 5 miles
Now, CE = \(\frac{7}{10}\)x BC = \(\frac{7}{10}\) x 5 = 3.5 miles
(v) (d) :Clearly the radio of areas of two angles (i,e \(\triangle A B C \sim \triangle D E C\))
\(\begin{array}{l} =\left(\frac{B C}{E C}\right)^{2}=\left(\frac{10}{7}\right)^{2}=\frac{100}{49} \\ \therefore \quad \text { Required ratio }=\frac{\operatorname{ar}(\Delta C D E)}{a r(E B A D)}=\frac{49}{100-49}=\frac{49}{51} \end{array}\)
Case Study Questions

























