CBSE 11th Standard Maths Subject HOT Questions 4 Mark Questions 2021 Part - I
By QB365 on 29 May, 2021
QB365 Provides the HOT Question Papers for Class 11 Maths, and also provide the detail solution for each and every HOT Questions. HOT Questions will help to get more idea about question pattern in every exams and also will help to get more marks in Exams
QB365 - Question Bank Software
CBSE 11th Standard Maths Subject HOT Questions 4 Mark Questions 2021 Part - I
11th Standard CBSE
-
Reg.No. :
Mathematics
-
Out of 100 students, 15 passed in English, 12 passed in Mathematics, 8 in Science, 4 in English and Science, 4 in all the three.Find how many students passed in English and Mathematics but not in Science?
(a) -
Two trees A and B are on the same side of a river. From a point C in the river the distance of trees A and B are 250m and 300m, respectively of the angle C is 450, find the distance between the trees.[use \(\sqrt { 2 } =1.44\)]
(a) -
Find the value of x and y, if \(\frac { \left( 1+i \right) x-2i }{ 3+i } +\frac { \left( 2-3i \right) y+i }{ 3-i } =i\)
(a) -
The area of a triangle is 5 sq units and two of its vertices are (2,1) and (3,-2).If third vertex is (x,y), where y=x+3, then find the coordinates of the third vertex.
(a) -
A box contains 4 red, 5 white and 6 black balls.A person draws 4 balls from the box at random.Find the probability of selecting atleast one ball of each colour.
(a)
*****************************************
CBSE 11th Standard Maths Subject HOT Questions 4 Mark Questions 2021 Part - I Answer Keys
-
n(E)=15,n(M)=12,n(s)=8,\(n(E\cap M)=6\)
\(n(M\cap S)=7,n(E\cap S)=4,n(E\cap M\cap S)=4\)
(i)\(n(E\cap M\cap \overline { S } )=n(E\cap M)-n(E\cap M\cap S)\)
=6-4=2 -
According to the given information,
we have the following
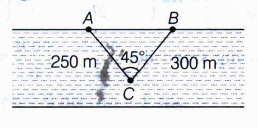
In \(\Delta \)ABC, by cosine rule,
we have
\({ AB }^{ 2 }={ AC }^{ 2 }+{ BC }^{ 2 }-2AC.BC\quad cos\frac { \pi }{ 4 } \)
\(\therefore \quad AB=\sqrt { { (250) }^{ 2 }+{ (300) }^{ 2 }-2\times 250\times 300\times \frac { 1 }{ \sqrt { 2 } } } \)
\(=\sqrt { 62500+90000-75000\sqrt { 2 } } \)
\(=\sqrt { 152500-75000\times 1.44 } \)
\(=\sqrt { 152500-108000 } =\sqrt { 44500 } =210.95m\) -
Given \(\frac { \left( 1+i \right) x-2i }{ 3+i } +\frac { \left( 2-3i \right) y+i }{ 3-i } =i\)
\(\Rightarrow \frac { x+\left( x-2 \right) i }{ 3+i } +\frac { 2y+\left( 1-3y \right) i }{ 3-i } =i\)
\(\Rightarrow \frac { \left[ x+\left( x-2 \right) i \right] \left( 3-i \right) +\left[ 2y+\left( 1-3y \right) i \right] \left( 3+i \right) }{ \left( 3+i \right) \left( 3-i \right) } =i\)
\(\Rightarrow \left( 4x+9y-3 \right) +i\left( 2x-7y-3 \right) =10i\)
\(\Rightarrow 4x+9y-3=0\quad and\quad 2x-7y-3=10\)
\(Ans.\ x=3\ and \ y=-1\) -
\(\frac { 1 }{ 2 } \left| x(1+2)+2(-2-y)+3(y-1) \right| =5 \Rightarrow \left| 3x+y-7 \right| =10\)
\(\Rightarrow \) 3x + y - 7 = 10 or 3x + y - 7 = -10 \(\Rightarrow \) 3x + 7 = 17
or 3x + 7 = -3
Case I When 3x + y = 17
It is given that y = x + 3 \(\Rightarrow \) x - y = -3
On solving Eqs.(i) and (ii) we ,get
\(x=\frac { 7 }{ 2 } and\quad y=\frac { 13 }{ 2 } \)
Case II when 3x + y = -3
On solving Eqs.(ii) and (iii), we get
\(x=\frac { -3 }{ 2 } and\quad y=\frac { 3 }{ 2 } \)
\(\left( \frac { 7 }{ 2 } ,\frac { 13 }{ 2 } \right) or\left( \frac { -3 }{ 2 } ,\frac { 3 }{ 2 } \right) \) -
Let A = event that 1 red, 2 white and 1 black balls are drawn,
B= event that 1 red, 2 white and 1 black balls are drawn and
C= event that 2 red, 1 white and 1 black balls are drawn.
Here A, B and C are munually exclusive events.
Hence, required probability
= P(A\(\cup \)B\(\cup \)C) = P(A) + P(B) + P(C)
Ans. \(\frac { 48 }{ 91 } \)



































