CBSE 11th Standard Maths Subject Introduction to Three Dimensional Geometry Ncert Exemplar 2 Marks Questions 2021
By QB365 on 27 May, 2021
QB365 Provides the NCERT Exemplar Question Papers for Class 11 Maths , and also provide the detail solution for each and every ncert exemplar papers. Ncert Exemplar papers will help to get more idea about question pattern in every exams and also will help to get more marks in Exams
QB365 - Question Bank Software
CBSE 11th Standard Maths Subject Introduction to Three Dimensional Geometry Ncert Exemplar 2 Marks Questions 2021
11th Standard CBSE
-
Reg.No. :
Mathematics
-
Let L,M,N be the feet of the perpendiculars drawn from a point P(3,4,5) on the X,Y and Z-axes respectively.Find the coordinates of L, M and N.
(a) -
Find the centroid of a triangle, the mid-point of whose sides are D(1, 2, -3), E (3, 0, 1) and F(-1, 1, -4).
(a) -
Find the point on X-axis which is equidistant from the points A(3,2,2) and B(5,5,4)
(a) -
Find the coordinates of a point equidistant from the four points O(0,0,0), A(l,0,0), B(0,m,0), and C(0,0,n)
(a) -
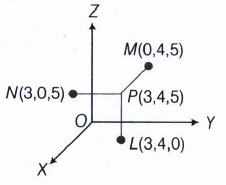
Let L,M,N be the feet of the perpendicules drawn from the point P (3,4,5) on the XY,YZ and ZX-planes, respectively. Find the distance of these points L,M,N from the point P.
(a)
2 Marks
*****************************************
CBSE 11th Standard Maths Subject Introduction to Three Dimensional Geometry Ncert Exemplar 2 Marks Questions 2021 Answer Keys
-
L(3,0,0), M(0,4,0) and N(0,0,5)
-
The centroid of a triangle is equal to the centroid of the triangle formed by mid-points of its sides.
(1, 1, -2)
-
Let the point on X-axis be P(x,0,0).
\(Then,\quad { (x-3) }^{ 2 }+{ (0-2) }^{ 2 }+{ (0-2) }^{ 2 }\)
\(={ (x-5) }^{ 2 }+{ (0-5) }^{ 2 }+{ (0-4) }^{ 2 }\)
\(Ans.\left( \frac { 49 }{ 4 } ,0,0 \right) \) -
\(Let\quad P(x,y,z)\quad be\quad required\quad point.\)
\(Then,\quad OP=PA=PB=PC\)
\(Now,\quad OP=PA\Rightarrow { OP }^{ 2 }={ PA }^{ 2 }\)
\(\Rightarrow { (0-x) }^{ 2 }+{ (0-y) }^{ 2 }+{ (0-z) }^{ 2 }={ x-1 }^{ 2 }+{ y-0 }^{ 2 }+{ (z-0) }^{ 2 }\)
\( \Rightarrow { x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }={ x }^{ 2 }-2lx+{ l }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }\)
\(\Rightarrow 2lx={ l }^{ 2 }\Rightarrow x=\frac { 1 }{ 2 } \)
\(Similarly,\quad OP=PB\Rightarrow y=\frac { m }{ 2 } and\quad OP=PC\Rightarrow x=\frac { n }{ 2 } \)
\(Hence,\quad the\quad coordinates\quad of\quad the\quad required\quad point\quad are\quad \left( \frac { 1 }{ 2 } ,\frac { m }{ 2 } ,\frac { n }{ 2 } \right) .\) -
L is the foot of perpendicular drwn from the point P(3,4,5) to the XY-plane.
Therefore, the coordinate of the point L are (3,4,0). The distance between the points (3,4,5) and (3,4,0) is 5 units. Similarly, the lengths of the foot of perpendiculars on YZ and ZX-planes are 3 and 4 units, respectively.
2 Marks



































