CBSE 11th Standard Maths Subject Trigonometric Functions HOT Questions 4 Mark Questions With Solution 2021
By QB365 on 29 May, 2021
QB365 Provides the HOT Question Papers for Class 11 Maths, and also provide the detail solution for each and every HOT Questions. HOT Questions will help to get more idea about question pattern in every exams and also will help to get more marks in Exams
QB365 - Question Bank Software
CBSE 11th Standard Maths Subject Trigonometric Functions HOT Questions 4 Mark Questions With Solution 2021
11th Standard CBSE
-
Reg.No. :
Mathematics
-
If \(cos\left( \alpha +\beta \right) =\frac { 4 }{ 5 } ,\quad sin(\alpha -\beta )=\frac { 5 }{ 13 } \) and \(\alpha , \beta \) lie between 0 and \(\frac { \pi }{ 4 } \) then prove that \(tan 2\alpha =\frac { 56 }{ 33 } .\)
(a) -
If \(\theta +\phi =\alpha \) and \(tan \theta =k\) \(tan\quad \phi ,\) then prove that \(sin\left( \theta -\phi \right) =\frac { k-1 }{ k+1 } sin\alpha .\)
(a) -
If tan(πcosθ)=cot(πsinθ) then prove that \(cos\left( \theta -\frac { \pi }{ 4 } \right) =\pm \frac { 1 }{ 2\sqrt { 2 } } .\)
(a) -
If \(cos \left( \theta +\phi \right) = m\quad cos\quad \left( \theta -\phi \right) \)then find the value of \(\frac { 1-m }{ 1+m } cot\quad \phi .\)
(a) -
Two trees A and B are on the same side of a river. From a point C in the river the distance of trees A and B are 250m and 300m, respectively of the angle C is 450, find the distance between the trees.[use \(\sqrt { 2 } =1.44\)]
(a)
*****************************************
CBSE 11th Standard Maths Subject Trigonometric Functions HOT Questions 4 Mark Questions With Solution 2021 Answer Keys
-
since, \(\alpha \),\(\beta \) lie between 0 and \(\frac { \pi }{ 4 } \)
\(\therefore -\frac { \pi }{ 4 } <\alpha -\beta \frac { \pi }{ 4 } and\quad 0<\alpha +\beta <\frac { \pi }{ 2 } \)
\(\Rightarrow cos\quad (\alpha -\beta )\quad and\quad sin\quad (\alpha +\beta )\quad are\quad positive.\)
\(Now,\quad sin\quad (\alpha +\beta )=\sqrt { 1-{ cos }^{ 2 }\left( \alpha +\beta \right) } =\frac { 3 }{ 5 } \)
\(and\quad \quad cos\quad (\alpha -\beta )=\sqrt { 1-{ sin }^{ 2 }\left( \alpha -\beta \right) } =\frac { 12 }{ 13 } \)
\(\therefore \quad tan\quad (\alpha +\beta )=\frac { sin\left( \alpha +\beta \right) }{ cos\left( \alpha +\beta \right) } =\frac { 3/5 }{ 4/5 } =\frac { 3 }{ 4 } \)
\(and\quad tan\quad (\alpha -\beta )=\frac { sin\quad \left( \alpha -\beta \right) }{ cos\quad \left( \alpha -\beta \right) } =\frac { 5/13 }{ 12/13 } =\frac { 5 }{ 12 }\)
\(now,\quad tan\quad 2\alpha =tan\quad [\left( \alpha +\beta \right) +\left( \alpha -\beta \right) ]\)
\(=\frac { tan\quad (\alpha +\beta )+tan\quad (\alpha -\beta ) }{ 1-tan\quad (\alpha +\beta )tan\left( \alpha -\beta \right) } =\frac { \frac { 3 }{ 4 } +\frac { 5 }{ 12 } }{ 1-\frac { 3 }{ 4 } \times \frac { 5 }{ 12 } } =\frac { 56 }{ 33 } \)
Hence proved. -
\(Given,\quad tan\quad \theta =k\quad tan\quad \phi \)
\(\Rightarrow \frac { tan\quad \theta }{ tan\quad \phi } =\frac { k }{ 1 } =\frac { tan\quad \theta +tan\quad \phi }{ tan\quad \theta -tan\quad \phi } =\frac { k+1 }{ k-1 } \) [applying componendo and dividendo]
\(\Rightarrow \frac { \frac { sin\quad \theta }{ cos\quad \theta } +\frac { sin\quad \phi }{ cos\quad \phi } }{ \frac { sin\quad \theta }{ cos\quad \theta } -\frac { sin\quad \phi }{ cos\quad \phi } } =\frac { k+1 }{ k-1 }\)
\(\Rightarrow \frac { sin\quad \theta .cos\quad \phi +cos\quad \theta .sin\quad \phi }{ sin\quad \theta .cos\quad \phi -cos\quad \theta .sin\quad \phi } =\frac { k+1 }{ k-1 }\)
\(\Rightarrow \frac { sin\quad \left( \theta +\phi \right) }{ sin\quad \left( \theta -\phi \right) } =\frac { k+1 }{ k-1 } \Rightarrow \frac { sin\quad \left( \theta -\phi \right) }{ sin\quad \left( \theta +\phi \right) } =\frac { k-1 }{ k+1 } \)
\(\Rightarrow sin\quad (\theta -\phi )=\frac { k-1 }{ k+1 } .sin\quad \alpha \)
Hence proved. -
\(\frac { sin\quad (\pi \quad cos\quad \theta ) }{ cos\quad (\pi \quad sin\quad \theta ) } =\frac { cos\quad (\pi \quad sin\quad \theta ) }{ sin\quad \left( \pi \quad sin\quad \theta \right) }\)
\(\Rightarrow cos\quad \left( \pi \quad cos\quad \theta \quad +\quad \pi \quad sin\quad \theta \right) =0\)
\(\Rightarrow cos\quad \theta \quad +\quad sin\quad \theta \quad =\quad \pm \frac { 1 }{ 2 }\)
\( \Rightarrow cos\quad \theta \quad cos\quad \frac { \pi }{ 4 } +sin\quad \theta \quad sin\quad \frac { \pi }{ 4 } =\pm \frac { 1 }{ 2\sqrt { 2 } } \)
\(\therefore \quad cos\left( \theta -\frac { \pi }{ 4 } \right) =\pm \frac { 1 }{ 2\sqrt { 2 } } \) -
We have, \(cos \left( \theta +\phi \right) = m\quad cos\left( \theta -\phi \right) \)
\(\Rightarrow \frac { 1 }{ m } =\frac { cos\left( \theta -\phi \right) }{ cos\left( \theta +\phi \right) } \)
Now, \(\frac { 1-m }{ 1+m } =\frac { cos\quad \left( \theta -\phi \right) -cos\quad \left( \theta +\phi \right) }{ cos\quad \left( \theta -\phi \right) +cos\left( \theta +\phi \right) } =tan\quad \theta \quad tan\quad \phi \\ \\ \)
Ans. tan \(\theta \). -
According to the given information,
we have the following
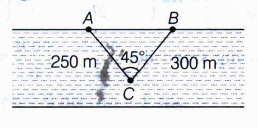
In \(\Delta \)ABC, by cosine rule,
we have
\({ AB }^{ 2 }={ AC }^{ 2 }+{ BC }^{ 2 }-2AC.BC\quad cos\frac { \pi }{ 4 } \)
\(\therefore \quad AB=\sqrt { { (250) }^{ 2 }+{ (300) }^{ 2 }-2\times 250\times 300\times \frac { 1 }{ \sqrt { 2 } } } \)
\(=\sqrt { 62500+90000-75000\sqrt { 2 } } \)
\(=\sqrt { 152500-75000\times 1.44 } \)
\(=\sqrt { 152500-108000 } =\sqrt { 44500 } =210.95m\)



































