CBSE 11th Standard Physics Subject HOT Questions 3 Mark Questions With Solution 2021
By QB365 on 29 May, 2021
QB365 Provides the HOT Question Papers for Class 11 Physics, and also provide the detail solution for each and every HOT Questions. HOT Questions will help to get more idea about question pattern in every exams and also will help to get more marks in Exams
QB365 - Question Bank Software
CBSE 11th Standard Physics Subject HOT Questions 3 Mark Questions With Solution 2021
11th Standard CBSE
-
Reg.No. :
Physics
-
It is a well-known fact that during a total solar eclipse the disk of the moon almost completely covers the disk of the sun. The distance of moon (rME) and sun (rSE) from the earth surface is 3.84 x 108 m and 1.496 x 1011 m while the diameter of Sun is 1.390 x 109 m. Determine the approximate diameter of the moon.
(a) -
State which of the following situations are possible and give an example for each of these?
(a) An object with a constant acceleration but with zero velocity.
(b) An object moving in a certain direction with acceleration in the perpendicular direction.(a) -
A body is projected vertically upwards from A, the top of a tower it reaches the ground in it t1 second.If it is projected vertically downwards from A with the same velocity it reaches the ground in t2 second.If it falls freely, from A, prove that it would reach the ground in \(\sqrt { { t }_{ 1 }{ t }_{ 2 } } \) second.
(a) -
The maximum height attained by a projectile is increased by 10% by increasing its speed of projection, without changing the angle of projection. What will the percentage increase in the horizontal range?
(a) -
The range of a rifle bullet is 1000m, when \(\theta \) is the angle of projection. If the bullet is fired with the same angle from a car travelling at 36km/h towards the target, show that the range will be increasing by 142.9\(\sqrt { tan\theta m } \).
When the bullet is fired from the moving car, the horizontal component velocity of the bullet increases with the velocity of car. But the vertical component of the velocity remains uneffected.(a) -
You may have seen in a circus a motorcyclist driving in vertical loops inside a death well (a hollow spherical chamber with holes, so the spectators can watch from outside). Explain clearly, why the motorcyclist does not drop down when he is at the uppermost point, with no support from below. What is the minimum speed required at the uppermost position to perform a vertical loop if the radius of the chamber is 25 m?
(a) -
Calculate the change in the energy of a 500 kg astellite when it falls from an altitude of 200 km to 199km.If this change takes place during one orbit.Calculate the retarding force on the satellite Given,mass of the earth = \(6\times { 10 }^{ 24 }kg\) and radius of the earth = 6400 km
(a) -
The brass scale of a barometer gives correct reading at 0 0C. Coefficient of linear expansion of brass is 2.0 x 10-5/0 C. The barometer reads 75.00 cm at 270 C. What is the true atmospheric pressure at 270 C.
(a) -
Calculate the total number of degrees of freedom possessed by the molecules in 1cm3 of H2 gas at temperature 273k and 1 atm pressure?
(a)
*****************************************
CBSE 11th Standard Physics Subject HOT Questions 3 Mark Questions With Solution 2021 Answer Keys
-
Distance of moon from the earth (rME ) = 3.84 \(\times \) 108 m
Distance of sun from the earth (rSE) = 1.496\(\times \) 1011m
Diameter of Sun (D) = 1.39 \(\times \) 109 m
During the total solar eclipse, the sun is completely covered by the disk of the moon.
\(\therefore\) Angular diameter of the moon = Angular diameter of the sun
\(\frac { d }{ { r }_{ ME } } =\frac { D }{ r_{ SE } } \)
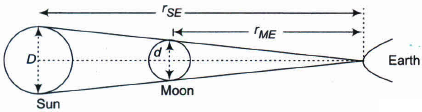
\(\therefore\) d = D\(\times \) \(\frac { { r }_{ ME } }{ r_{ SE } } \) = 1.39\(\times \)109\(\times \)\(\frac { 3.84\times 10^{ 8 } }{ 1.496\times { 10 }^{ 11 } } \)
= 3.5679\(\times \)106 m = 3567.9\(\times \)103 = 3567.9 km -
(a) When an object is projected upwards, its velocity at the top-most point is zero even though the acceleration on it is 9.8m/s2(g).
(b) When a stone tied to a string is whirled in a circular path, the acceleration acting on it is always at right angles i.e. perpendicular to the direction of motion of stone (we will study about it in chapter 'motion in a plane'). -
Using relations
Consider upwards as negative and downwards as positive.
\(h=-u{ t }_{ 1 }+\frac { 1 }{ 2 } g{ t }_{ 1 }^{ 2 }.............(i)\)
\(\\ h=u{ t }_{ 2 }+\frac { 1 }{ 2 } g{ t }_{ 2 }^{ 2 }...............(ii)\)
\(\\ On \ substracting \ Eqs. \ (i) \ from \ (ii), \ we \ get\)
\(\\ or \ 0=({ t }_{ 2 }+{ t }_{ 1 })+\frac { 1 }{ 2 } g{ t }_{ 2 }^{ 2 }-\frac { 1 }{ 2 } g{ t }_{ 1 }^{ 2 }\)
\(\\ or\ u({ t }_{ 2 }+{ t }_{ 1 })+\frac { 1 }{ 2 } g({ t }_{ 2 }+{ t }_{ 1 })({ t }_{ 2 }-{ t }_{ 1 })=0\)
\(\\ or\ u+\frac { 1 }{ 2 } g({ t }_{ 2 }+{ t }_{ 1 })=0\)
\(\\ or \ u=-\frac { g }{ 2 } ({ t }_{ 2 }-{ t }_{ 1 }).........(iii)\)
\(\\ From \ Eqs \ (i) \ and \ (iii), \ we \ get\)
\(\\ Now,\quad h=\frac { g{ t }_{ 1 } }{ 2 } ({ t }_{ 2 }-{ t }_{ 1 })+\frac { 1 }{ 2 } g{ t }_{ 1 }^{ 2 }=\frac { 1 }{ 2 } g{ t }_{ 1 }{ t }_{ 2 }.....(iv)\)
\(\\ Again, \ when \ the \ body \ falls \ freely.\)
\(\\ h=\frac { 1 }{ 2 } g{ t }^{ 2 };\frac { 1 }{ 2 } g{ t }_{ 1 }{ t }_{ 2 }=\frac { 1 }{ 2 } g{ t }^{ 2 }\quad [fron\quad eq.iv]\)
\(\\ or\quad t=\sqrt { { t }_{ 1 }{ t }_{ 2 } } \quad Hence\quad proved\) -
As, maximum height, H = \(\frac { { u }^{ 2 } }{ 2g } { sin }^{ 2 }\theta \)
Consider \(\triangle \)H b ethe increase in H when u changes by \(\triangle \)u, it can be obtained by differentiating the above equation, we get
\(\triangle H=\frac { 2u\triangle u{ sin }^{ 2 }\theta }{ 2g } =\frac { 2\triangle u }{ u } H\)
\(\\ \Rightarrow \frac { \triangle H }{ H } =\frac { 2\triangle u }{ u } \)
Given % increasing in H is 10% so
\(\frac { \triangle H }{ H } =\frac { 10 }{ 100 } =0.1\Rightarrow \frac { 2\triangle u }{ u } =0.1\)
\(\\ As,\quad R=\frac { { u }^{ 2 }sin2\theta }{ g } \)
\(\\ \because \quad \triangle R=\frac { 2u\triangle u }{ u } sin2\theta \Rightarrow \frac { \triangle R }{ R } =\frac { 2\triangle u }{ u } =0.1\)
\(\\ \therefore \ increase \ in \ horizontal \ range=\frac { \triangle R }{ R } \times 100\)
= 0.1 x 100
= 10% -
Given, R = 1000m
Horizontal range of the bullet fired at an angle \(\theta \) is
\(R=\frac { { u }^{ 2 }sin2\theta }{ g } \Rightarrow 1000=\frac { { u }^{ 2 }sin\theta cos\theta }{ g } ....(i)\)
Bullet is fired from the car moving with 36km/h
i.e.10m/s, then horizontal component of the velocity of = usin\(\theta \) + 10
Vertical component of the velocity of the bullet=usin\(\theta \)
Then, new range of the bullet is
\({ R }_{ 1 }=\frac { 2 }{ g } (usin\theta )(ucos\theta +10)\)
\(\\ =\frac { 2 }{ g } { u }^{ 2 }sin\theta cos\theta +\frac { 20 }{ g } usin\theta \Rightarrow { R }_{ 1 }=R+\frac { 20 }{ g } usin\theta\)
\( \\ \Rightarrow { R }_{ 1 }-R=\frac { 20 }{ g } usin\theta ....(ii)\)
\(\\ From\ Eq.(i),we \ have \ u=\sqrt { \frac { 1000\times g }{ 2sin\theta cos\theta } } .....(iii)|\)
\(\\ Now, \ substituting \ the \ value \ of \ u \ in \ Eq.(ii), \ we \ get\ \)
\(\\ { R }_{ 1 }-R=\frac { 20 }{ g } \sqrt { \frac { 1000\times g }{ 2sin\theta cos\theta } } sin\theta =20\sqrt { \frac { 500\times sin\theta }{ gcos\theta } }\)
\( \\ =20\sqrt { \frac { 500 }{ 9.8 } tan\theta } =142.9\sqrt { tan\theta } \) -
When the motorcyclist is at the uppermost point of the death well, then weight of the cyclist, as well as the normal reaction R of the ceiling of the chamber, is in downward direction. These forces are balanced by the outward centrifugal force acting on the motorcyclist
\(\therefore \\ \) \(Rg+mg=\frac { { mv }^{ 2 } }{ r }\)
Where, v = Speed of the motorcyclist
m = mass of (motorcycle + driver)
r = radius of the death well.
As the forces acting on the motorcyclist are balanced, therefore, motorcyclist does not fall down.
The minimum speed required to perform a vertical loop is given by
\(mg=\frac { mv^{ 2 }min }{ r }\)
[\(\because \\ \) In the case weight of the object = centripetal force]
or vmin =\(\sqrt { rg } =\sqrt { 25\times 9.8 } =15.65{ m }/{ s }\) -
Given
\({ M }_{ e }=6\times { 10 }^{ 24 }kg,{ r }_{ e }=6400km\)
\( { r }_{ 1 }=6400+200=6600km=6.6\times { 10 }^{ 6 }m\)
\({ r }_{ 2 }=6400+199=6599km=6.599\times { 10 }^{ 6 }m\)
Change in energy = \(GMm\left( \frac { 1 }{ { r }_{ 1 } } -\frac { 1 }{ { r }_{ 2 } } \right) \)
\(\\ =6.67\times `{ 10 }^{ -11 }\times 6\times { 10 }^{ 24 }\times 500\)
\( \left( \frac { 1 }{ 6.6\times { 10 }^{ 6 } } =\frac { 1 }{ 6.599\times { 10 }^{ 6 } } \right) \)
\(\\ =2\times { 10 }^{ 17 }(1.5152\times { 10 }^{ -7 }-1.5154\times { 10 }^{ 7 })J\)
\(=-4\times { 10 }^{ 6 }J\)
If this occurs during one orbit,then the energy lost = \(force\times distance\) .If we take the sistances as being the circumference of one orbit Then
Retarding force
\(=\frac { 4\times { 10 }^{ 6 } }{ 2\pi \times 6.6\times { 10 }^{ 6 } } =\frac { 4\times { 10 }^{ 6 } }{ 2\times 6.6\times 3.14\times { 10 }^{ 6 } } =0.1N\) -
As the brass scale of a barometer gives correct reading at T1 = 00 C , hence at temperature T2 = 270 C., the scale will expand and will not give correct reading
In such, true value
= Observed scale reading x\((1+\alpha \triangle T)\)
True pressure = 75.00 cm x [1 + 2.0 x 10-5 x (27 - 0)]
= 75 x (1 + 2.0 x 10-5 x 27]
= 75.00(1 + 54 x 10-5) cm = 75.04 cm -
At 273 K temperature and 1 atm pressure mean STP condition.
\(\therefore \) Number of H2 molecules on 22400cm3 at STP = 6.02 x 1023
Number of H2 molecules on 1cm3 at STP = \(\frac { 6.02\times { 10 }^{ 23 } }{ 22400 } =2.6875\times { 10 }^{ 19 }\)
\(\therefore \) Number of degrees of freedom associated with each H2 (diatomic) molecule = 5
\(\therefore \) Total number of degrees of freedom associated with 1cm3 of gas = 2.6875 x 1019 x 5 = 1.34375 x 1020



































