CBSE 11th Standard Physics Subject Ncert Exemplar 5 Mark Questions 2021 Part - I
By QB365 on 26 May, 2021
QB365 Provides the updated NCERT Exemplar Questions for Class
11, and also provide the detail solution for each and every NCERT Exemplar questions. NCERT Exemplar questions are latest updated question pattern from NCERT, QB365 will helps to get more marks in Exams
QB365 - Question Bank Software
CBSE 11th Standard Physics Subject Ncert Exemplar 5 Mark Questions 2021 Part - I
11th Standard CBSE
-
Reg.No. :
Physics
-
It is a common observation that rain clouds can be at about a kilometre altitude above the ground.
(a) If a rain drop falls from such a height freely under gravity, what will be its speed?Also, calculate in km/h (g = 10 m/s2).
(b) A typical rain drop is about 4 mm diameter.Momentum is mass x speed in magnitude.Estimate its momentum when it hits ground.
(c) Estimate time required to flatten the drop.
(d) Rate of change of momentum is force.Estimate how much force such a drop would exert on you?
(e) Estimate the order of magnitude force on umbrella. Typical lateral separation between two rain drops is 5cm.(a) -
A girl riding a bicycle along a straight road with a speed of 5 m/ s throws a stone of mass 0.5 kg which has a speed of 15 m /s with respect to the ground along her direction of motion. The mass of the girl and bicycle is 50 kg. Does the speed of the bicycle change after the stone is thrown ? What is the change in speed, if so ?
(a) -
Figure shows (x, t), (y, t) diagram of a particle moving in 2-dimensions.
-Q.png)
-Q.png)
If the particle has a mass of 500 g, find the force (direction and magnitude) acting on the particle.(a) -
(a) A child stands at the centre of a turntable with his two arms outstretched. The turntable is set rotating with an angular speed of 40 rev/min. How much is the angular speed of the child if he folds his hands back and thereby reduces his moment of inertia to 2/5 times the initial value ? Assume that the turntable rotates without friction.
(b) Show that the child’s new kinetic energy of rotation is more than the initial kinetic energy of rotation. How do you account for this increase in kinetic energy?(a) -
The Young's modulus for stell is much more than that for rubber. For the same longitudinal strain, which one will have greater tensile stress?
(a) -
Consider a Carnot cycle operating between T1 = 500K and T2 = 300K producing 1KJ of mechanical work per cycle. Find the heat transferred to/by the engine by/to the reservoir.
(a) -
A gas mixture consists of 2.0 moles of oxygen and 4.0 moles of neon at temperature T. Neglecting all vibrational modes, calculate the total internal energy of the system. (oxygen has two rotational modes)
(a) -
For the harmonic travelling wave \(y=2\cos { 2\pi } \left( 10t-0.0080x+3.5 \right) \) , where, x and y are in cm and t is in second. What is the phase difference between the oscillatory motion at two points separated by a distance of \(\frac { 3\lambda }{ 4 } \)(at a given instant in time)?
(a) -
A solid sphere rolls down two different inclined planes of the same heights but different angles of inclination.
(a) Will it reach the bottom with the same speed in each case?
(b) Will it take longer to roll down one plane than the other?
(c) If so, which one and why?(a) -
The oxygen molecule has a mass of 5.30 × 10-26 kg and a moment of inertia of 1.94 × 10-46 kg m2 about an axis through its centre perpendicular to the lines joining the two atoms. Suppose the mean speed of such a molecule in a gas is 500 m/s and that its kinetic energy of rotation is two thirds of its kinetic energy of translation. Find the average angular velocity of the molecule.
(a)
*****************************************
CBSE 11th Standard Physics Subject Ncert Exemplar 5 Mark Questions 2021 Part - I Answer Keys
-
(a) Here, height(h)=1 km = 1000m, g = 10m/s2
Velocity attained by the rain drop in freely falling through a height h.
\(v=\sqrt { 2gh } =\sqrt { 2\times 10\times 1000 }\)
\( \\ =100\sqrt { 2 } m/s\)
\(\\ =100\sqrt { 2 } \times \frac { 60\times 60 }{ 1000 } Km/h\)
\(\\ =360\sqrt { 2 } km/h\approx 510km/h\)
(b) Diameter of the drop(d) = 2r = 4mm
Radius of the drop(r) = 2mm = 2 x 10-3m
Mass of a rain drop(m)=Vx\(\rho \)
\(=\frac { 4 }{ 3 } \pi { r }^{ 3 }\rho =\frac { 4 }{ 3 } \times \frac { 22 }{ 7 } \times (2\times { 10 }^{ -3 })^{ 3 }\times { 10 }^{ 3 }\)
\( \approx 3.4\times { 10 }^{ -5 }kg\)
\(\\ Momentum \ of \ the \ rain \ drop(\rho )=mv \)
\(\\ =3.4\times { 10 }^{ -5 }\times 100\sqrt { 2 }\)
\(\\ \approx 4.7\times { 10 }^{ -3 }{ kg }^{ -m/s }\)
(c) Time required to flatten the drop
= time taken by the drop to travel the distance equal to the diameter of the drop near the ground
\(t=\frac { d }{ v } =\frac { 4\times { 10 }^{ -3 } }{ 100\sqrt { 2 } } =0.028\times { 10 }^{ -3 }s\)
\(\\ =2.8\times { 10 }^{ -5 }s\)
(d) Force exerted by a rain drop
\(F=\frac { Change \ in \ momentum }{ Time } \)
\(=\frac { \rho -0 }{ t } =\frac { 4.7\times { 10 }^{ -3 } }{ 2.8\times { 10 }^{ -5 } } \approx 168N\)
(e) Radius of the umbrella(R) = \(\frac { 1 }{ 2 } m\)
\(\therefore \ Area \ of \ the \ umbrella(A)=\pi { R }^{ 2 }\)
\(\\ =\frac { 22 }{ 7 } \times { (\frac { 1 }{ 2 } ) }^{ 2 }=\frac { 22 }{ 28 } =\frac { 11 }{ 14 } \approx 0.8{ m }^{ 2 }\)
Number of drops striking the umbrella simultaneously with average of 5cm or 5 x 10-2m
\(=\frac { 0.8 }{ { (5\times { 10 }^{ -2 }) }^{ 2 } } =320\)
Net force exerted on umbrella
= 320 x 168 = 53760 N -
Total mass of girl, bicycle and stone, m1 = ( 50 + 0.5 ) kg = 50.5 kg
Velocity of bicycle, u1 = 5 m/ s
Mass of stone, m2 = 0.5 kg
Velocity of stone, u2 = 15 m /s
Mass of girl and bicycle, m = 50 kg
Yes, the speed of the bicycle changes after the stone is thrown.
Let, after throwing the stone the speed of bicycle be \(\nu \) m /s.
According to the law of conservation of linear momentum,
m1u1 = m2u2 + m\(\nu \)
50.5 x 5 = 0.5 x 15 + 50 x \(\nu \)
252.5 - 705 = 50\(\nu \) or \(\nu \) = \(\frac { 245.0 }{ 50 } \)
\(\nu \) = 4.9 m/ s
Change in speed = 5 - 4.9 = 0.1 m / s -
Given, mass of the particle (m) = 500 g = 0.5 kg
x-t graph of the particle is a straight line.
Hence, particle is moving with a uniform velocity along x-axis, i. e. its acceleration along x-axis is zero and hence, force acting along x-axis is zero.
y- t graph of particle is a parabola. Therefore, particle is in accelerated motion along y-axis.
At t = 0, uy= 0
Along y-axis, at t = 2s, y =4m
Using equation of motion,
\(y={ u }_{ y }t+\frac { 1 }{ 2 } { a }_{ y }{ t }^{ 2 }\)
\(\\ 4=0\times 2+\frac { 1 }{ 2 } \times { a }_{ y }\times { (2) }^{ 2 }\)
\(\\ { a }_{ y }=2m/{ s }^{ 2 }\)
Force acting y-axis (fy) = may
\(0.5\times 2=1.0N\) (along y-axis) -
(a) As no external torque is involved with child + turntable system, so angular momentum of system remains constant.
or \({ I }_{ i }{ \omega }_{ i }={ I }_{ f }{ \omega }_{ f }\)
\({ I }_{ i }{ \omega }_{ i }\) = initial angular momentum, \({ I }_{ f }{ \omega }_{ f }\) = final angular momentum
Here, \({ \omega }_{ i }=40\quad rpm\Rightarrow { I }_{ f }=\frac { 2 }{ 5 } { I }_{ i }\)
Substituting, we get
\({ I }_{ i }\times40=\frac { 2 }{ 5 } { I }_{ i }\times{ \omega }_{ f }\)
or \({ \omega }_{ f }=\frac { 5\times40 }{ 2 } =100\quad rpm\)
(b) \(\frac{\text { Final Kinetic Energy of rotation }}{\text { Initial Kinetic Energy of rotation }}=\frac{\frac{1}{2} I_{2} \omega_{2}^{2}}{\frac{1}{2} I_{1} \omega_{1}^{2}}=\frac{\frac{1}{2} I_{2}\left(2 \pi v_{2}\right)^{2}}{\frac{1}{2} I_{1}\left(2 \pi v_{1}\right)^{2}}\)
\(=\frac{I_{2} v_{2}^{2}}{I_{1} v_{1}^{2}}=\frac{\frac{2}{5} I_{1} \times(100)^{2}}{\frac{2}{5} I_{1} \times(40)^{2}}\)
= 2.5
Clearly, final (K.E) becomes more because the child used his internal energy when he folds his hands to increase the kinetic energy. -
Young's modulus \((Y)=\frac { Stress }{ Longitudinal\ strain } \)
For same longitudinal strain \(Y\alpha stress\)
\(\frac { { Y }_{ stress } }{ { Y }_{ rubber } } =\frac { { (stress) }_{ steel } }{ { (stress) }_{ rubber } } \)
But \({ Y }_{ steel }>{ Y }_{ rubber }\)
\(\frac { { Y }_{ steel } }{ { Y }_{ rubber } } >1\)
Therefore from Eq(i) we get
\(\frac { { (stress) }_{ steel } }{ { (stress) }_{ rubber } } >1\)
\(or { (stress) }_{ steel }>(stress)_{ rubber }\) -
Here, T1 = 500K, T2 = 300K, W = 1KJ = 1000J
As, efficiency, \(\eta =\frac { W }{ Q } =\frac { { T }_{ 1 }-{ T }_{ 2 } }{ { T }_{ 1 } } \)
So, heat transferred to engine by the reservoir in cycle
\(Q_{ 1 }=\frac { W{ T }_{ 1 } }{ { T }_{ 1 }-{ T }_{ 2 } } =\frac { 1000\times 500 }{ 500-300 } =2500J\quad or\quad 2.5kJ\)
and heat transferred by the engine to the cold reservoir in one cycle
Q2 = Q1 - W = 2.5kJ- 1kJ = 1.5kJ -
O2 has five degrees of freedom.
Therefore, energy pre mole = \(\frac { 5 }{ 2 } RT\)
For 2 moles of O2, energy = 5RT
Neon has three degrees of freedom
Energy per mole = \(\frac { 3 }{ 2 } RT\)
For 4 moles of neon, energy
\(=4\times \frac { 3 }{ 2 } RT=6RT\)
Total eneryg = 5RT + 6RT = 11RT. -
Given equation is \(y=2\cos { 2\pi } \left( 10t-0.0080x+3.5 \right) \)
Comparing with standard equation,
\(y=2\cos { 2\pi } \left( 10t-0.0080x+3.5 \right)\)
\( y=a\cos { \left( \omega t-kx+\phi \right) } \)
\(a=2cm,\omega =\frac { 2\pi }{ T } =20\pi ,\quad T=0.1s\)
\(\\ k=\frac { 2\pi }{ \lambda } =0.008\times 2\pi \Rightarrow \lambda =\frac { 2\pi }{ 2\pi \times 0.008 } =1.25m\)
\(\\ \phi =2\pi \times 3.5=7\pi rad\)
When x = \(\frac { 3\lambda }{ 4 } \); \({ \phi }_{ 4 }=\frac { 2\pi }{ \lambda } \times \frac { 3\lambda }{ 4 } =\frac { 3\pi }{ 2 } rad\). -
(a) Using law of conservation of energy
\(\frac { 1 }{ 2 } mv^{ 2 }+\frac { 1 }{ 2 } I{ \omega }^{ 2 }\)=mgh
or \(\frac { 1 }{ 2 } mv^{ 2 }+\frac { 1 }{ 2 } \left( \frac { 2 }{ 5 } m{ R }^{ 2 } \right) \frac { { v }^{ 2 } }{ { R }^{ 2 } } =mgh\)
or \(\frac { 7 }{ 10 } v^{ 2 }=gh\) or v =\(\sqrt { \frac { 10gh }{ 7 } } \)
Since h is same for both the inclined planes therefore v is the same
(b)
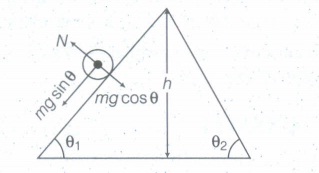
\(l=\frac { 1 }{ 2 } \left( \frac { g\quad sin\quad \theta }{ 1+\frac { { K }^{ 2 } }{ { R }^{ 2 } } } \right) { t }^{ 2 }=\frac { g\quad sin\theta }{ 2\left( 1+\frac { 2 }{ 5 } \right) } { t }^{ 2 }=\frac { 5gsin\theta }{ 14 } { t }^{ 2 }\)
or \(t=\sqrt { \frac { 14l }{ 5g\quad sin\quad \theta } } \)
Now, sin \(\theta\)=\(\frac { h }{ l } \) or l =\(\frac { h }{ sin\theta } \)
∴ \(t=\frac { 1 }{ sin\quad \theta } \sqrt { \frac { 14h }{ 5g } } \)
Lesser the value of,\(\theta\) more will be t.
(c) Clearly, the solid sphere will take longer to roll down the plane with smaller inclination. -
Here, m = 5.30\(\times\)10-26 kg
I = 1.94\(\times\)10-46kg m2
v =500 m/s
If \(\frac { m }{ 2 } \)is mass of each atom of oxygen and 2r is distance between the two atoms as shown in Fig.then
\(I=\frac { m }{ 2 } { r }^{ 2 }+\frac { m }{ 2 } { r }^{ 2 }={ mr }^{ 2 }\)
\(r=\sqrt { \frac { 1 }{ m } } =\sqrt { \frac { 1.94\times { 10 }^{ -46 } }{ 5.30\times { 10 }^{ -26 } } } \)
= 0.61\(\times\)10-10 m
As K.E. of rotation= \(\frac { 2 }{ 3 } \)K.E of translation
∴ \(\frac { 1 }{ 2 } I{ \omega }^{ 2 }=\frac { 2 }{ 3 } \times \frac { 1 }{ 2 } { m\omega }^{ 2 }\)
\(\frac { 1 }{ 2 } ({ mr }^{ 2 }){ \omega }^{ 2 }=\frac { 1 }{ 2 } { mv }^{ 2 }\)
\(\omega =\sqrt { \frac { 2 }{ 3 } } \frac { \upsilon }{ r } =\sqrt { \frac { 2 }{ 3 } } \times \frac { 500 }{ 0.61\times { 10 }^{ -10 } } \) = 6.7 1012 rad/s



































