CBSE 12th Standard Maths Subject Matrices Case Study Questions 2021
By QB365 on 21 May, 2021
QB365 Provides the updated CASE Study Questions for Class 12 Maths, and also provide the detail solution for each and every case study questions . Case study questions are latest updated question pattern from NCERT, QB365 will helps to get more marks in Exams
QB365 - Question Bank Software
CBSE 12th Standard Maths Subject Matrices Case Study Questions 2021
12th Standard CBSE
-
Reg.No. :
Maths
-
In a city there are two factories A and B. Each factory produces sports clothes for boys and girls. There are three types of clothes produced in both the factories, type I, II and III. For boys the number of units of types I, II and III respectively are 80, 70'and 65 in factory A and 85, 65 and 72 are in factory B. For girls the number of units of types I, II and III respectively are 80, 75, 90 in factory A and 50, 55, 80 are in factory B.
Based on the above information, answer the following questions.
(i) If P represents the matrix of number of units of each type produced by factory A for both boys and girls, then P is given by
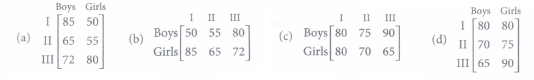
(ii) If Q represents the matrix of number of units of each type produced by factory B for both boys and girls, then Q is given by
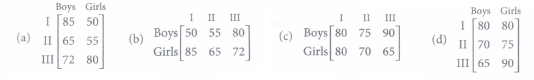
(iii) The total- production of sports clothes of each type for boys is given by the matrix
(iv) The total production of sports clothes of each type for girls is given by the matrix
(v) Let R be a 3 x 2 matrix that represent the total production of sports clothes of each type for boys and girls, then transpose of R is(iv) The total production of sports clothes of each type for girls is given by the matrix
(a) -
Three car dealers, say A, Band C, deals in three types of cars, namely Hatchback cars, Sedan cars, SUV cars. The sales figure of 2019 and 2020 showed that dealer A sold 120 Hatchback, 50 Sedan, 10 SUV cars in 2019 and 300 Hatchback, 150 Sedan, 20 SUV cars in 2020; dealer B sold 100 Hatchback, 30 Sedan,S SUV cars in 2019 and 200 Hatchback, 50 Sedan, 6 SUV cars in 2020; dealer C sold 90 Hatchback, 40 Sedan, 2 SUV cars in 2019 and 100 Hatchback, 60 Sedan,S SUV cars in 2020.
Based on the above information, answer the following questions.
(i) The matrix summarizing sales data of 2019 is
(ii) The matrix summarizing sales data of 2020 is
(iii) The total number of cars sold in two given years, by each dealer, is given by the matrix
(iv) The increase in sales from 2019 to 2020 is given by the matrix
(v) If each dealer receive profit of Rs. 50000 on sale of a Hatchback, Rs. 100000 on sale of a Sedan and Rs. 200000 on sale of a SUV (v) then amount of profit received in the year 2020 by each dealer is given by the matrix.
(a) -
Three schools A, Band C organized a mela for collecting funds for helping the rehabilitation of flood victims. They sold hand made fans, mats and plates from recycled material at a cost of Rs. 25, Rs.100 and Rs.50 each. The number of articles sold by school A, B, C are given below.
Artilcle\School A B C Fans 40 25 35 Mats 50 40 50 Plates 20 30 40 Based on above information, answer the following questions.
(i) If P be a 3 x 3 matrix represent the sale of handmade fans, mats and plates by three schools A, Band C, then
(ii) If Q be a 3 x 1 matrix represent the sale prices (in Rs) of given products per unit, then
(iii) The funds collected by school A by selling the given articles is(a) Rs. 7000 (b) Rs. 6125 (c) Rs. 7875 (d) Rs. 8000 (iv) The funds collected by school B by selling the given articles is
(a) Rs. 5125 (b) Rs. 6125 (c) Rs. 7125 (d) Rs. 8125 (v) The total funds collected for the required purpose is
(a) Rs. 20000 (b) Rs. 21000 (c) Rs. 30000 (d) Rs. 35000 (a) -
A manufacturer produces three types of bolts, x, y and z which he sells in two markets. Annual sales (in Rs) are indicated below:
Markets Products x y z I 10000 2000 18000 II 6000 20000 8000 If unit sales prices of x, y and z are Rs.2.50, Rs.1.50 and Rs.1.00 respectively, then answer the following questions using the concept of matrices.
(i) Find the total revenue collected from the Market-I.(a) Rs. 44000 (b) Rs. 48000 (c) Rs. 46000 (d) Rs. 53000 (ii) Find the total revenue collected from the Market-II.
(a) Rs. 5100 (b) Rs. 5300 (c ) Rs. 46000 (d) Rs. 49000 (iii) If the unit costs of the above three commodities are Rs.2.00, Rs.1.00 and 50 paise respectively, then find the gross profit from both the markets.
(a) Rs. 53000 (b) Rs. 46000 (c) Rs. 34000 (d) Rs. 32000 (iv) If matrix \(4=\left[a_{i j}\right]_{2 \times 2}\) , where \(a_{i j}=1, \text { if } i \neq j\) , and \(a_{i j}=0 \text { if } i=j\) , then A2 is equal to
(a) I (b) A (c) 0 (d) none of these (v) If A and B are matrices of same order, then (AB' - BA') is a
(a) skew-symmetric matrix (b) null matrix (c) symmetric matrix (d) unit matrix (a) -
If \(A=\left[a_{i j}\right]_{m \times n} \text { and } B=\left[b_{i j}\right]_{m \times n}\) are two matrices, then \(A \pm B\) is of order m x n and is defined as \((A \pm B)_{i j}=a_{i j} \pm b_{i j}\), where i = 1,2, , m and j = 1,2, ..., n
If \(A=\left[a_{i j}\right]_{m \times n} \text { and } B=\left[b_{j k}\right]_{n \times p}\) are two matrices, then AB is of order m x p and is defined as \((A B)_{i k}=\sum_{r=1}^{n} a_{i r} b_{r k}=a_{i 1} b_{1 k}+a_{i 2} b_{2 k}+\ldots . .+a_{i n} b_{n k}\)
Consider \(A=\left[\begin{array}{cc} 2 & -1 \\ 3 & 4 \end{array}\right], B=\left[\begin{array}{ll} 5 & 2 \\ 7 & 4 \end{array}\right], C=\left[\begin{array}{ll} 2 & 5 \\ 3 & 8 \end{array}\right] \text { and } D=\left[\begin{array}{ll} a & b \\ c & d \end{array}\right]\)
Using the concept of matrices answer the following questions.
(i) Find the product AB.(a) \(\left[\begin{array}{cc} 3 & 0 \\ 43 & 22 \end{array}\right]\) (b) \(\left[\begin{array}{cc} 0 & 3 \\ 22 & 43 \end{array}\right]\) (c) \(\left[\begin{array}{cc} 43 & 22 \\ 0 & 3 \end{array}\right]\) (d) \(\left[\begin{array}{cc} 22 & 43 \\ 3 & 0 \end{array}\right]\) (ii) If A and B are any other two matrices such that AB exists, then
(a) BA does not exist (b) BA will be equal to AB (c) BA mayor may not exist (d) None of these (iii) Find the values of a and c in the matrix D such than CD - AB = 0.
(a) a = 77, c=-191 (b) a = -191, c=77 (c) a = 191, c=77 (d) a = 91, c = 70 (iv) Find the values of band d in the matrix D such that CD - AB = 0.
(a) b = 44, d = -110 (b) b = 110, d = 44 (c) b = -110, d = 44 (d) b = -44, d = 110 (v) Find B + D.
(a) \(\left[\begin{array}{cc} 80 & 200 \\ 115 & 105 \end{array}\right]\) (b) \(\left[\begin{array}{cc} 84 & 48 \\ 180 & 181 \end{array}\right]\) (c) \(\left[\begin{array}{ll} 186 & 108 \\ -84 & -48 \end{array}\right]\) (d) \(\left[\begin{array}{cc} -186 & -108 \\ 84 & 48 \end{array}\right]\) (a)
Case Study Questions
*****************************************
CBSE 12th Standard Maths Subject Matrices Case Study Questions 2021 Answer Keys
-
(I) (d) : In factory A, number of units of types I, II and III for boys are 80, 70, 65 respectively and for girls number of units of types I, II and III are 80, 75, 90 respectively.
(ii) (a) : In factory B, number of units of types I, II and III for boys are 85, 65, 72 respectively and for girls number of units of types I, II and III are 50, 55, 80 respectively.
(iii) (c) : Let X be the matrix that represent the number of units of each type produced by factory A for boys, and Y be the matrix that represent the number of units of each type produced by factory B for boys.
Then, X = \(\begin{array}{ccc} \text { I } & \text { II } & \text { III } \\ {[170} & 130 & 130] \end{array}\) and Y = \(\begin{array}{ccc} \text { I } & \text { II } & \text { III } \\ {[85} & 65 & 72] \end{array}\)
Now, required matrix = X + Y = [80 70 65] + [85 65 72]
= [165 135 137]
(iv) (a): Required matrix = [80 75 90] + [50 55 80]
= [130 130 170]
(v) (a) : Clearly,R = P+Q
\(=\left[\begin{array}{ll} 80 & 80 \\ 70 & 75 \\ 65 & 90 \end{array}\right]+\left[\begin{array}{ll} 85 & 50 \\ 65 & 55 \\ 72 & 80 \end{array}\right]=\left[\begin{array}{ll} 165 & 130 \\ 135 & 130 \\ 137 & 170 \end{array}\right]\)
\(\therefore \quad R^{\prime}=\left[\begin{array}{lll} 165 & 135 & 137 \\ 130 & 130 & 170 \end{array}\right]\) -
(i) (b) : In 2019,dealer A sold 120 Hatchback, 50 Sedan and 10 SUV; dealer B sold 100 Hatchback, 30 Sedan and 5 SUV and dealer C sold 90 Hatchback, 40 Sedan and 2 SUV
\(\therefore\) Required matrix, say P, is given by
(ii) (a) : In 2020,
dealer A sold 300 Hatchback, 150 Sedan, 20 SUV
dealer B sold 200 Hatchback, 50 sedan, 6 SUV
dealer C sold 100 Hatchback, 60 sedan,S SUV
\(\therefore\) Required matrix, say Q, is given by
(iii) (c) : Total number of cars sold in two given years, by each dealer, is given by
(iv) (c): The increase in sales from 2019 to 2020 is given by
(v) (c) : The amount of profit in 2020 received by each dealer is given by the matrix
\(\begin{array}{c} A \\ B \\ C \end{array}\left[\begin{array}{c} 15000000+15000000+4000000 \\ 10000000+5000000+1200000 \\ 5000000+6000000+1000000 \end{array}\right]\)
\(\begin{array}{r} A \\ =B \\ C \end{array}\left[\begin{array}{l} 34000000 \\ 16200000 \\ 12000000 \end{array}\right]\) -
(i) (a) : Clearly,
(ii) (d) : Since Q is a 3 x 1 matrix, therefore
(iii) (a) : Clearly, total funds collected by each school is given by the matrix.
\(P Q=\left[\begin{array}{ccc} 40 & 50 & 20 \\ 25 & 40 & 30 \\ 35 & 50 & 40 \end{array}\right]\left[\begin{array}{c} 25 \\ 100 \\ 50 \end{array}\right]\)
\(=\left[\begin{array}{c} 1000+5000+1000 \\ 625+4000+1500 \\ 875+5000+2000 \end{array}\right]=\left[\begin{array}{l} 7000 \\ 6125 \\ 7875 \end{array}\right]\)
\(\therefore\) Funds collected by school A is Rs. 7000
Funds collected by school B is Rs. 6125
Pimds collected by school C is Rs. 7875
(iv) (b)
(v) (b) : Total funds collected for the required purpose
= Rs. (7000 + 6125 + 7875) = Rs. 21000 -
Let A be the 2 x 3 matrix representing the annual sales of products in two markets.
Let B be the column matrix representing the sale price of each unit of products x, y, z.
\(\therefore \quad B=\left[\begin{array}{c} 2.5 \\ 1.5 \\ 1 \end{array}\right]\)
Now, revenue = sale price x number of items sold
\(=\left[\begin{array}{ccc} 10000 & 2000 & 18000 \\ 6000 & 20000 & 8000 \end{array}\right]\left[\begin{array}{c} 2.5 \\ 1.5 \\ 1 \end{array}\right]\)
\(=\left[\begin{array}{l} 25000+3000+18000 \\ 15000+30000+8000 \end{array}\right]=\left[\begin{array}{l} 46000 \\ 53000 \end{array}\right]\)
Therefore, the revenue collected from Market I = Rs.46000 and the revenue collected from Market II = Rs. 53000.
(i) (c)
(ii) (b)
(iii) (d) : Let C be the column matrix representing cost price of each unit of products x, y, z.
Then, \(C=\left[\begin{array}{c} 2 \\ 1 \\ 0.5 \end{array}\right]\)
\(\therefore\) Total cost in each market is given by
\(A C=\left[\begin{array}{ccc} 10000 & 2000 & 18000 \\ 6000 & 20000 & 8000 \end{array}\right]\left[\begin{array}{c} 2 \\ 1 \\ 0.5 \end{array}\right]\)
\(=\left[\begin{array}{c} 20000+2000+9000 \\ 12000+20000+4000 \end{array}\right]=\left[\begin{array}{l} 31000 \\ 36000 \end{array}\right]\)
Now, Profit matrix = Revenue matrix, Cost matrix
\(=\left[\begin{array}{l} 46000 \\ 53000 \end{array}\right]-\left[\begin{array}{l} 31000 \\ 36000 \end{array}\right]=\left[\begin{array}{l} 15000 \\ 17000 \end{array}\right]\)
Therefore, the gross profit from both the markets
= Rs.15000+ Rs.17000= Rs.32000
(iv) (a) : We have \(A=\left[\begin{array}{ll} 0 & 1 \\ 1 & 0 \end{array}\right]\)
\(\therefore \quad A^{2}=\left[\begin{array}{ll} 0 & 1 \\ 1 & 0 \end{array}\right]\left[\begin{array}{ll} 0 & 1 \\ 1 & 0 \end{array}\right]=\left[\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right]=I\)
(v) (a) : We have, (AB' -BA')' = (B')'A' - (A')'B'
= BA' - AB' = -(AB' - BA')
Thus, AB' - BA' is a skew-symmetric matrix. -
(i) (a) : \(A B=\left[\begin{array}{cc} 2 & -1 \\ 3 & 4 \end{array}\right]\left[\begin{array}{ll} 5 & 2 \\ 7 & 4 \end{array}\right]\)
\(=\left[\begin{array}{cc} 10-7 & 4-4 \\ 15+28 & 6+16 \end{array}\right]=\left[\begin{array}{cc} 3 & 0 \\ 43 & 22 \end{array}\right]\)
(ii) (c)
(iii) (b) : We have, CD - AB = 0
\(\Rightarrow\left[\begin{array}{ll} 2 & 5 \\ 3 & 8 \end{array}\right]\left[\begin{array}{ll} a & b \\ c & d \end{array}\right]-\left[\begin{array}{cc} 3 & 0 \\ 43 & 22 \end{array}\right]=\left[\begin{array}{ll} 0 & 0 \\ 0 & 0 \end{array}\right]\)
\(\Rightarrow\left[\begin{array}{ll} 2 a+5 c & 2 b+5 d \\ 3 a+8 c & 3 b+8 d \end{array}\right]-\left[\begin{array}{cc} 3 & 0 \\ 43 & 22 \end{array}\right]=\left[\begin{array}{ll} 0 & 0 \\ 0 & 0 \end{array}\right]\)
\(\Rightarrow\left[\begin{array}{cc} 2 a+5 c-3 & 2 b+5 d \\ 3 a+8 c-43 & 3 b+8 d-22 \end{array}\right]=\left[\begin{array}{ll} 0 & 0 \\ 0 & 0 \end{array}\right]\)
By equality of matrices, we get 2a + 5c - 3 = 0 ...(i)
3a + 8c - 43 = 0 ...(ii)
2b + 5d = 0 ...(iii)
3b + 8d - 22 = 0 ...(iv)
Solving (i) and (ii), we get a = -191, e = 77
(iv) (c) : Solving (iii) and (iv), we get b = -110, d = 44
(v) (d) : Wehave, \(B+D=\left[\begin{array}{ll} 5 & 2 \\ 7 & 4 \end{array}\right]+\left[\begin{array}{cc} -191 & -110 \\ 77 & 44 \end{array}\right]\)
\(=\left[\begin{array}{cc} -186 & -108 \\ 84 & 48 \end{array}\right]\)
Case Study Questions






































