CBSE 12th Standard Maths Subject Three Dimensional Geometry Case Study Questions 2021
By QB365 on 21 May, 2021
QB365 Provides the updated CASE Study Questions for Class 12 Maths, and also provide the detail solution for each and every case study questions . Case study questions are latest updated question pattern from NCERT, QB365 will helps to get more marks in Exams
QB365 - Question Bank Software
CBSE 12th Standard Maths Subject Three Dimensional Geometry Case Study Questions 2021
12th Standard CBSE
-
Reg.No. :
Maths
-
A football match is organised between students of class XII of two schools, say school A and school B. For which a team from each school is chosen. Remaining students of class XII of school A and B are respectively sitting on the plane represented by the equation \(\vec{r} \cdot(\hat{i}+\hat{j}+2 \hat{k})=5 \text { and } \vec{r} \cdot(\hat{i}-\hat{j}+\hat{k})=6\) ,to cheer up the team of their respective schools.

Based on the above information, answer the following questions.
(i) The cartesian equation of the plane on which students of school A are seated is(a) 2x - y +z = 8 (b) 2x + y + z = 8 (c) x + y + 2z = 5 (d) x + y + z = 5 (ii) The magnitude of the normal to the plane on which students of school B are seated, is
(a) \(\sqrt 5\) (b) \(\sqrt 6\) (c) \(\sqrt 3 \) (d) \(\sqrt 2\) (iii) The intercept form of the equation of the plane on which students of school B are seated, is
(a) \(\frac{x}{6}+\frac{y}{6}+\frac{z}{6}=1\) (b) \(\frac{x}{3}+\frac{y}{(-6)}+\frac{z}{6}=1\) (c) \(\frac{x}{3}+\frac{y}{6}+\frac{z}{6}=1\) (d) \(\frac{x}{3}+\frac{y}{6}+\frac{z}{3}=1\) (iv) Which of the following is a student of school B?
(a) Mohit sitting at (1, 2, 1) (b) Ravi sitting at (0,1,2) (c) Khushi sitting at (3, 1, 1) (d) Shewta sitting at (2, -1, 2) (v) The distance of the plane, on which students of school B are seated, from the origin is
(a) 6 units (b) \(\frac{1}{\sqrt{6}}\) units (c) \(\frac{5}{\sqrt{6}}\) units (d) \(\sqrt 6\) units (a) -
Consider the following diagram, where the forces in the cable are given.
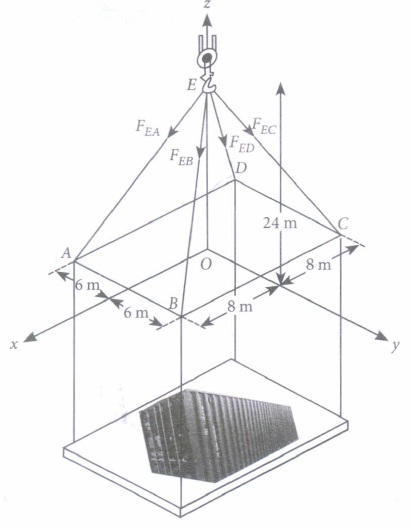
Based on the above information, answer the following questions.
(i) The cartesian equation of line along EA is\((a) \ \frac{x}{-4}=\frac{y}{3}=\frac{z}{12}\) \((b) \ \frac{x}{-4}=\frac{y}{3}=\frac{z-24}{12}\) \((c) \ \frac{x}{-3}=\frac{y}{4}=\frac{z-12}{12}\) \((d) \ \frac{x}{3}=\frac{y}{4}=\frac{z-24}{12}\) (ii) The vector \(\overline{E D}\) is
(a) \(8 \hat{i}-6 \hat{j}+24 \hat{k}\) (b) \(-8 \hat{i}-6 \hat{j}+24 \hat{k}\) (c) \(-8 \hat{i}-6 \hat{j}-24 \hat{k}\) (d) \(8 \hat{i}+6 \hat{j}+24 \hat{k}\) (iii) The length of the cable EB is
(a) 24 units (b) 26 units (c) 27 units (d) 25 units (iv) The length of cable EC is equal to the length of
(a) EA (b) EB (c) ED (d) All of these (v) The sum of all vectors along the cables is
(a) \(96 \hat{i}\) (b) \(96 \hat{j}\) (c) \(-96 \hat{k}\) (d) \(96 \hat{k}\) (a) -
The Indian Coast Guard (lCG) while patrolling, saw a suspicious boat with four men. They were nowhere looking like fishermen. The soldiers were closely observing the movement of the boat for an opportunity to seize the boat. They observe that the boat is moving along a planar surface. At an instant of time, the coordinates of the position of coast guard helicopter and boat are (2, 3, 5) and (1, 4, 2) respectively.
Based on the above information, answer the following questions.
(i) If the line joining the positions of the helicopter and boat is perpendicular to the plane in which boat moves, then equation of plane is(a) x-y+3z = 2 (b) x+y+3z = 2 (c) x - y + 3z = 3 (d) x + y + 3z = 3 (ii) If the soldier decides to shoot the boat at given instant of time, where the distance measured in metres, then what is the distance that bullet has to travel?
(a) \(\sqrt 5\) m (b) \(\sqrt 8\) m (c) \(\sqrt 10\) m (d) \(\sqrt 11\) m (iii) If the speed of bullet is 30 m/sec, then how much time will the bullet take to hit the boat after the shot is fired?
(a) 30 seconds (b) 1 second (c) \(\frac{1}{2}\) second (d) \(\frac{\sqrt{11}}{30}\) m (iv) At the given instant of time, the equation of line passing through the positions of helicopter and boat is
(a) \(\frac{x}{1}=\frac{y}{-1}=\frac{z}{3}\) (b) \(\frac{x-1}{1}=\frac{y-4}{-1}=\frac{z-2}{3}\) (c) \(\frac{x}{1}=\frac{y}{1}=\frac{z}{-3}\) (d) \(\frac{x-1}{1}=\frac{y-4}{1}=\frac{z-2}{-3}\) (v) At a different instant of time, the boat moves to a different position along the planar surface. What should be the coordinates of the location of the boat for the bullet to hit the boat if soldier shoots the bullet along the line whose equation is \(\frac{x-1}{1}=\frac{y-1}{-2}=\frac{z-2}{3} ?\)
(a) \(\left(\frac{1}{2}, \frac{1}{2}, \frac{1}{2}\right)\) (b) \(\left(\frac{3}{4}, \frac{3}{2}, \frac{5}{4}\right)\) (c) \(\left(\frac{1}{3}, \frac{1}{4}, \frac{1}{5}\right)\) (d) none of these (a) -
The equation of motion of a rocket are: x = 2t, y = -4t, z = 4t, where the time 't' is given in seconds, and the distance measured is in kilometres.
Based on the above information, answer the following questions.
(i) What is the path of the rocket?(a) Straight line (b) Circle (c) Parabola (d) none of these (ii) Which of the following points lie on the path of the rocket?
(a) (0, 1, 2) (b) (1, -2, 2) (c) (2, -2, 2) (d) none of these (iii) At what distance will the rocket be from the starting point (0, 0, 0) in 10 seconds?
(a) 40 km (b) 60 km (c) 30 km (d) 80 km (iv) If the position of rocket at certain instant of time is (3, -6, 6), then what will be the height of the rocket from the ground, which is along the xy-plane?
(a) 3km (b) 2km (c) 4km (d) 6km (v) At certain instant of time, if the rocket is above sea level, where equation of surface of sea is given by 3x - y + 4z = 2 and position of rocket at that instant of time is (1, -2,2), then the image of position of rocket in the sea is
(a) \(\left(\frac{20}{13}, \frac{15}{13}, \frac{18}{13}\right)\) (b) \(\left(\frac{-20}{13}, \frac{-15}{13}, \frac{-18}{13}\right)\) (c) \(\left(\frac{20}{13}, \frac{-15}{13}, \frac{18}{13}\right)\) (d) none of these (a) -
A mobile tower stands at the top of a hill. Consider the surface on which tower stand as a plane having points A(0, 1,2), B(3, 4, -1) and C(2, 4, 2) on it. The mobile tower is tied with 3 cables from the point A, Band C such that it stand vertically on the ground. The peak of the tower is at the point (6, 5, 9), as shown in the figure.
Based on the above information, answer the following questions
(i) The equation of plane passing through the points A, Band C is(a) 3x - 4y + z = 0 (b) 3x - 2y + z = 0 (c) 4x - 3y + z = 0 (d) 4x - 3y + 3z = 0 (ii) The height of the tower from the ground is
(a) 6 units (b) 5 units (c) \( \frac{17}{\sqrt{14}} units\) (d) \((d) \frac{5}{\sqrt{14}} units\) (iii) The equation of line of perpendicular drawn from the peak of tower to the ground is
(a) \( \frac{x-6}{3}=\frac{y-4}{-2}=\frac{z-9}{1}\) (b) \( \frac{x-6}{3}=\frac{y-5}{-2}=\frac{z-9}{1}\) (c) \(\frac{x-6}{3}=\frac{y-4}{2}=\frac{z-9}{1}\) (d) none of these (iv) The coordinates of foot of perpendicular drawn from the peak of tower to the ground are
(a)\( \left(\frac{33}{14}, \frac{104}{14}, \frac{109}{14}\right) \) (b) \(\left(\frac{33}{14}, \frac{109}{14}, \frac{104}{14}\right)\) (c)\(\left(\frac{33}{14}, \frac{105}{14}, \frac{109}{14}\right)\) (d) none of these (v) The area of \(\Delta\)ABC is
(a) \(\frac{1}{2} \sqrt{14} \text { sq. units }\) (b) \(\frac{3}{2} \sqrt{14} \mathrm{sq} \text { units }\) (c) \(\sqrt{14} \mathrm\ {sq}.\ units\) (d)\(2\sqrt{14} \mathrm\ {sq}.\ units\) (a)
Case Study Questions
*****************************************
CBSE 12th Standard Maths Subject Three Dimensional Geometry Case Study Questions 2021 Answer Keys
-
(i) (c): Clearly, the plane for students of school A is \(\vec{r} \cdot(\hat{i}+\hat{j}+2 \hat{k})=5,\) which can be rewritten as
\((x \hat{i}+y \hat{j}+z \hat{k}) \cdot(\hat{i}+\hat{j}+2 \hat{k})=5\)
\(\Rightarrow \quad x+y+2 z=5\), which is the required cartesian equation.
(ii) (b): Clearly, the equation of plane for students of school B is \(\vec{r} \cdot(2 \hat{i}-\hat{j}+\hat{k})=6,\) which is of the form \(\vec{r} \cdot \vec{n}=d\)
∴ Normal vector to the plane is, \(\vec{n}=2 \hat{i}-\hat{j}+\hat{k}\) and its magnitude is \(|\vec{n}|=\sqrt{2^{2}+(-1)^{2}+1^{2}}=\sqrt{6}\)
(iii) (b): The cartesian form is 2x - y + z = 6, which can be rewritten as
\(\frac{2 x}{6}-\frac{y}{6}+\frac{z}{6}=1 \Rightarrow \frac{x}{3}+\frac{y}{(-6)}+\frac{z}{6}=1\)
(iv) (c): Since, only the point (3, I, 1) satisfy the equation of plane representing seating position of students of school B, therefore Khushi is the student of school B.
(v) (d): Equation of plane representing students of school B is \(\vec{r} \cdot(2 \hat{i}-\hat{j}+\hat{k})=6,\) which is not in normal form, as \(|\vec{n}| \neq 1\)
On dividing both sides by \(\sqrt{2^{2}+(-1)^{2}+1^{2}}=\sqrt{6}\), we get \(\vec{r} \cdot\left(\frac{2}{\sqrt{6}} \hat{i}-\frac{1}{\sqrt{6}} \hat{j}+\frac{1}{\sqrt{6}} \hat{k}\right)=\frac{6}{\sqrt{6}}\)
which is of the form \(\vec{r} \cdot \hat{n}=d\)
Thus, the required distance is \(\sqrt 6\) units. -
(i) (b): Clearly, the coordinates of A are (8, -6, 0) and that of E are (0, 0, 24).
Also, cartesian equation of line along EA is given by
\(\frac{x-0}{8-0}=\frac{y-0}{-6-0}=\frac{z-24}{0-24}\)
\(\Rightarrow \frac{x}{8}=\frac{y}{-6}=\frac{z-24}{-24} \Rightarrow \frac{x}{-4}=\frac{y}{3}=\frac{z-24}{12}\)
(ii) (c): Clearly, the coordinates of Dare (-8, -6, 0) and that of E are (0, 0, 24)
\(\therefore \text { Vector } \overline{E D} \text { is }(-8-0) \hat{i}+(-6-0) \hat{j}+(0-24) \hat{k} \ \text { i.e., }-8 \hat{i}-6 \hat{i}-24 \hat{k} \)
(iii) (b): Since, the coordinates of Bare (8, 6, 0) and that of E are (0, 0, 24), therefore length of cable
\(E B=\sqrt{(8-0)^{2}+(6-0)^{2}+(0-24)^{2}} \)
\(=\sqrt{64+36+576}=\sqrt{676}=26 \text { units }\)
(iv) (d): Since, the coordinates of Care (-8,6,0) therefore length of cable EC = \(\sqrt{(-8-0)^{2}+(6-0)^{2}+(0-24)^{2}}\)
\(=\sqrt{64+36+576}=\sqrt{676}=26 \mathrm{units}\)
Similarly, length of cable EA = ED = 26 units.
(v) (c): Sum of all vectors along the cables
\(=\overrightarrow{E A}+\overrightarrow{E B}+\overrightarrow{E C}+\overline{E D}\)
\( =(8 \hat{i}-6 \hat{j}-24 \hat{k})+(8 \hat{i}+6 \hat{j}-24 \hat{k})+(-8 \hat{i}+6 \hat{j}-24 \hat{k})+(-8 \hat{i}-6 \hat{j}-24 \hat{k}) \)
\(=-96 \hat{k}\) -
(i) (c) : Let P(2, 3, 5) and Q(1, 4, 2) be the positions of helicopter and boat respectively.
Now, direction ratios of PQ are proportional to 1-2, 4-3, 2-5, i.e , -1, 1,-3.
So, equation of plane passing through Q(1, 4, 2) and perpendicular to PQ is
-(x - 1) + (y - 4) + (-3) (z - 2) = 0 ⇒ x - y + 3z = 3
(ii) (d) : Required distance = Distance between P and Q
\(=\sqrt{(1-2)^{2}+(4-3)^{2}+(2-5)^{2}}=\sqrt{1+1+9}=\sqrt{11} \mathrm{~m}\)
(iii) (d) : We know, Distance = Speed x Time
ஃ Required time = \(\frac{\sqrt{11}}{30}\) seconds
(iv) (b) : Equation of line PQ is \(\frac{x-1}{1}=\frac{y-4}{-1}=\frac{z-2}{3}\)
(v) (b) : Any point on the line \(\frac{x-1}{1}=\frac{y-1}{-2}=\frac{z-2}{3}\) given by \((\lambda+1,-2 \lambda+1,3 \lambda+2)\)
Now, on substituting this point in the equation of plane x - y + 3z = 3, we get
\( (\lambda+1)-(-2 \lambda+1)+3(3 \lambda+2)=3 \)
\(\Rightarrow \lambda+1+2 \lambda-1+9 \lambda+6=3 \Rightarrow 12 \lambda=-3\)
\(\Rightarrow \ \lambda=\frac{-1}{4}\)
Thus, the required point is \(\left(\frac{-1}{4}+1, \frac{1}{2}+1, \frac{-3}{4}+2\right)\) i.e.,\(\left(\frac{3}{4}, \frac{3}{2}, \frac{5}{4}\right)\)
-
(i) (a): Eliminating 't' from the given equations, we get equation of path as, \(\frac{x}{2}=\frac{y}{-4}=\frac{z}{4} \text { or } \frac{x}{1}=\frac{y}{-2}=\frac{z}{2}\).
Thus, the path of the rocket represents a straight line.
(ii).(b) : Since, only (1, -2, 2) satisfy the equation of path of rocket therefore (1, -2, 2) lie on the path of rocket.
(iii) (b): For t = 10 sec, we have x = 20,y = -40, z = 40
Now, required distance = \(\sqrt{x^{2}+y^{2}+z^{2}}\)
\(=\sqrt{20^{2}+(-40)^{2}+(40)^{2}}=\sqrt{400+1600+1600}\)
\(=\sqrt{3600}=60 \mathrm{~km}\)
(iv) (d) : Clearly, height of rocket from the ground = z-coordinate of given position = 6 km
(v) (b) : Let Q be the image of point P(1, -2, 2) in the plane 3x - y + 4z = 2. Then, equation of PQ is
\(\frac{x-1}{3}=\frac{y+2}{-1}=\frac{z-2}{4}\)
Let the coordinates of Q be (3r +1, -r - 2, 4r + 2).
Let R be the mid -point of PQ. Then, coordinates of R are
\(\left(\frac{3 r+2}{2}, \frac{-r-4}{2}, \frac{4 r+4}{2}\right) \text { or }\left(\frac{3}{2} r+1, \frac{-r}{2}-2,2 r+2\right)\)
Since, R lies on 3x - y + 4z = 2.
\( \therefore \quad 3\left(\frac{3}{2} r+1\right)-\left(\frac{-r}{2}-2\right)+4(2 r+2)=2 \)
\(\Rightarrow \frac{9 r}{2}+3+\frac{r}{2}+2+8 r+8=2 \\ \)
\(\Rightarrow 13 r+13=2 \Rightarrow r=\frac{-11}{13}\)
Hence, the coordinates of Q are
\(\left(\frac{-33}{13}+1, \frac{11}{13}-2, \frac{-44}{13}+2\right) \text { i.e., }\left(\frac{-20}{13}, \frac{-15}{13}, \frac{-18}{13}\right)\) -
(i) (b) : The equation of plane passing through three non - collinear points is given by
\(\left|\begin{array}{ccc} x-x_{1} & y-y_{1} & z-z_{1} \\ x_{2}-x_{1} & y_{2}-y_{1} & z_{2}-z_{1} \\ x_{3}-x_{1} & y_{3}-y_{1} & z_{3}-z_{1} \end{array}\right|=0\)
\(\Rightarrow\left|\begin{array}{ccc} x & y-1 & z-2 \\ 3-0 & 4-1 & -1-2 \\ 2-0 & 4-1 & 2-2 \end{array}\right|=0\)
\(\Rightarrow\left|\begin{array}{ccc} x & y-1 & z-2 \\ 3 & 3 & -3 \\ 2 & 3 & 0 \end{array}\right|=0\)
\( \Rightarrow \ln x(0+9)-(y-1)(0+6)+(z-2)(9-6)=0 \)
\(\Rightarrow 9 x-6 y+6+3 z-6=0 \Rightarrow 3 x-2 y+z=0\)
(ii) (c) : Height of tower = Perpendicular distance from the point (6, 5, 9) to the plane 3x - 2y + z = 0
\(=\left|\frac{18-10+9}{\sqrt{3^{2}+(-2)^{2}+1^{2}}}\right|=\frac{17}{\sqrt{14}} \text { units }\)
(iii) (b) : D.R.'s of perpendicular are < 3, -2, 1 >
[ஃ Perpendicular is parallel to the normal to the plane] Since, perpendicular is passing through the point (6, 5, 9), therefore its equation is
\(\frac{x-6}{3}=\frac{y-5}{-2}=\frac{z-9}{1}\)
(iv) (a) : Let the coordinates of foot of perpendicular are
Since, this point lie on the plane 3x - 2y + z = 0, therefore we get, \((3 \lambda+6,-2 \lambda+5, \lambda+9)\)
\( 3(3 \lambda+6)-2(-2 \lambda+5)+(\lambda+9)=0 \)
\(\Rightarrow 9 \lambda+4 \lambda+\lambda+18-10+9=0 \)
\(\Rightarrow 14 \lambda=-17 \Rightarrow \lambda=\frac{-17}{14}\)
Thus, the coordinates of foot of perpendicular are
\(\left(\frac{-51}{14}+6, \frac{34}{14}+5, \frac{-17}{14}+9\right) \text { i.e., }\left(\frac{33}{14}, \frac{104}{14}, \frac{109}{14}\right)\)
(v) (b) : Clearly, area of ABC =\(\frac{1}{2}|\overrightarrow{A B} \times \overrightarrow{A C}|\)
\( =\frac{1}{2}|(3 \hat{i}+3 \hat{j}-3 \hat{k}) \times(2 \hat{i}+3 \hat{j})| \)
\(=\frac{1}{2}\left\|\begin{array}{cc} \hat{i} & \hat{j} & \hat{k} \\ 3 & 3 & -3 \\ 2 & 3 & 0 \end{array}\right\|=\frac{1}{2}|9 \hat{i}-6 \hat{j}+3 \hat{k}|\)
\( =\frac{1}{2} \sqrt{9^{2}+6^{2}+3^{2}}=\frac{1}{2} \sqrt{126}=\frac{3}{2} \sqrt{14} \text { sq. units } \)
Case Study Questions






































