We have
\(\vec{a}=5 \hat{i}+2 \hat{j}-4 \hat{k} \text { and } \vec{b}=3 \hat{i}+2 \hat{j}-8 \hat{k}\)
Therefore, the vector equation of the line is
\(\vec{r}=5 \hat{i}+2 \hat{j}-4 \hat{k}+\lambda(3 \hat{i}+2 \hat{j}-8 \hat{k})\)
Now, \(\vec{r}\) is the position vector of any point P(x, y, z) on the line.
\(x \hat{i}+y \hat{j}+z \hat{k}=5 \hat{i}+2 \hat{j}-4 \hat{k}+\lambda(3 \hat{i}+2 \hat{j}-8 \hat{k})\)
\(=(5+3 \lambda) \hat{i}+(2+2 \lambda) \hat{j}+(-4-8 \lambda) \hat{k}\)
Eliminating \(\lambda\), we get
\(\frac{x-5}{3}=\frac{y-2}{2}=\frac{z+4}{-8}\)

Substitute in (i) we get \(\frac { x }{ 3\alpha } +\frac { y }{ 3\beta } +\frac { z }{ 3\gamma } =1\Rightarrow \frac { x }{ \alpha } +\frac { y }{ \beta } +\frac { z }{ \gamma } =3\)

Since \(l, m, n \text { and } l+\delta l, m+\delta m, n+\delta n\) are direction cosines of a variable line in two different positions,therefore,
\(l^{2}+m^{2}+n^{2}=1\)
\(\text { and }(l+\delta l)^{2}+(m+\delta m)^{2}+(n+\delta n)^{2}=1\)
\(\text { Now, }(l+\delta l)^{2}+(m+\delta m)^{2}+(n+\delta n)^{2}=1\)
\(\Rightarrow\left(l^{2}+m^{2}+n^{2}\right)+2(l \cdot \delta l+m \cdot \delta m+n \cdot \delta n) \)
\(+(\delta l)^{2}+(\delta m)^{2}+(\delta n)^{2}=1[\text { from }(i i)] \)
\(\Rightarrow 1+2(l \delta l+m \delta m+n \delta n)+(\delta l)^{2} \)
\(+(\delta m)^{2}+(\delta n)^{2}=1[\text { using }(i)] \)
\(\Rightarrow 2(l \delta l+m \delta m+n \delta n)=-\left[(\delta l)^{2}+(\delta m)^{2}+(\delta n)^{2}\right] \)
\(\Rightarrow(l \delta l+m \delta m+n \delta n)=-\frac{1}{2}\left[(\delta l)^{2}+(\delta m)^{2}+(\delta n)^{2}\right] \)
\(\text { Also } \cos (\delta \theta)=l(l+\delta l)+m(m+\delta m)+n(n+\delta) \)
\(=\left(l^{2}+m^{2}+n^{2}\right)+(l \delta l+m \delta m+n \delta n) \)
\(=1-\frac{1}{2}\left[(\delta l)^{2}+(\delta m)^{2}+(\delta n)^{2}\right] \quad[\text { using }(i) \text { and (iii)] }\)
\(\Rightarrow 2(1-\cos \delta \theta)=(\delta I)^{2}+(\delta m)^{2}+(\delta n)^{2}\)
\(\Rightarrow 2 \times 2 \sin ^{2} \frac{\delta \theta}{2}=(\delta l)^{2}+(\delta m)^{2}+(\delta n)^{2}\)
\(\left[\because 1-\cos 2 \theta=2 \sin ^{2} \theta\right]\)
\(\Rightarrow 4\left[\frac{\delta \theta}{2}\right]^{2}=(\delta l)^{2}+(\delta m)^{2}+(\delta n)^{2}\)
\(\text { [if } \theta \text { is small, then } \sin \theta \rightarrow \theta]\)
\(\Rightarrow(\delta \theta)^{2}=(\delta l)^{2}+(\delta m)^{2}+(\delta n)^{2} \)
which is true.

(a) Let P be the given point (1, 6, 3) and M, the foot of perpendicular from P on the given line AB
  \(i.e.\quad \frac { x }{ 1 } =\frac { y-1 }{ 2 } =\frac { z-2 }{ 3 } (=k(say))\)

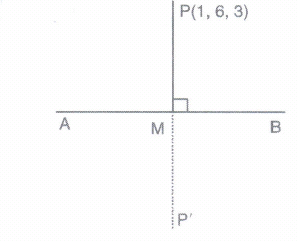
Any point on the given line is:
(k , 1+ 2k , 2 + 3k).
For some value of k, let the point be M.
:. Direction-ratios of PM are:
< k - 1 , 1 + 2k - 6, 2 + 3k - 3 >
i.e. < k - 1, 2k - 5, 3k - 1 > .
Since \(PM\bot AB\)  ,
:. (1) (k-l) + (2) (2k- 5) + (3) (3k-l) = 0
\(\Rightarrow\)k - 1 + 4k - 10 + 9k - 3 = 0
\(\Rightarrow\) 14k = 14 \(\Rightarrow\) k = 1.
:. Foot of perpendicular Mis (1,1+2,2+3) i.e. (1,3,5).
Let \(P'(\alpha ,\beta ,\gamma )\)  be the image of P in the given line.
Then M is the mid-point of [PP']
\(\frac { \alpha +1 }{ 2 } =1\frac { \beta +6 }{ 2 } =3,\frac { \gamma +3 }{ 2 } =5\)
\(\alpha +1=2,\beta +6=6,\gamma +3=10\)
\(\Rightarrow \alpha =1,\beta =0,\gamma =7\)
Hence the reqd image is(1,0,7).
(b) (i) The equations of PP' are:
\(\frac { x-1 }{ 1-1 } =\frac { y-6 }{ 0-6 } =\frac { z-3 }{ 7-3 } \)
\(i.e.\quad \frac { x-1 }{ 0 } =\frac { y-6 }{ -6 } =\frac { z-3 }{ 4 } \)
\(\Rightarrow \frac { x-1 }{ 1-1 } =\frac { y-6 }{ -3 } =\frac { z-3 }{ 2 } \)
(ii) Length od segment [PP']
\(\sqrt { { \left( 1-1 \right) }^{ 2 }+{ \left( 0-6 \right) }^{ 2 }+{ \left( 7-3 \right) }^{ 2 } } \)
\(=\sqrt { 0+36+16 } =\sqrt { 52 } =2\sqrt { 13 } units.\)

If lines intersect then \(\left(\vec{a}_{2}-\overrightarrow{a_{1}}\right) \cdot\left(\vec{b}_{1} \times \overrightarrow{b_{2}}\right)=0\)
\(\text { i.e. }\left|\begin{array}{ccc} 4-1 & 1-2 & 0-3 \\ 2 & 3 & 4 \\ 5 & 2 & 1 \end{array}\right|=0 \)
\(\Rightarrow 3(3-8)+1(2-20)-3(4-15)=0 \)
\(\Rightarrow-15-18+33=0, \text { true }\)
Hence, the lines intersect
For point of intersection, take general points on the two
\(\text {lines as }(2 \lambda+1,3 \lambda+2,4 \lambda+3)\text { and }(5 \mu+4,2 \mu+1, \mu)\)
If lines intersect then for same values \(\lambda \text { and } \mu \text {. }\)
\(2 \lambda+1=5 \mu+4 \Rightarrow 2 \lambda-5 \mu=3 \)
\(3 \lambda+2=2 \mu+1 \Rightarrow 3 \lambda-2 \mu=-1 \)
\(4 \lambda+3=\mu \Rightarrow 4 \lambda-\mu=-3\)
Solving \((i i) \text { and (iii) for } \lambda, \mu \text {, we get }\)
\(\lambda=-1, \mu=-1\)
Substituting in (iv), we get -4+1 = -3 true
Hence, for \(\lambda=-1, \mu=-1 \) the lines intersect.
Substituting in \( (i) \text {, for } \lambda=-1 \text {, }\)
Point of intersection is \( (-2+1,-3+2,-4+3) \text {, i.e }(-1,-1,-1) \)