CBSE 12th Standard Physics Subject Alternating Current Ncert Exemplar 3 Mark Questions 2021
By QB365 on 24 May, 2021
QB365 Provides the updated NCERT Exemplar Questions for Class 12, and also provide the detail solution for each and every case study questions. NCERT Exemplar questions are latest updated question pattern from NCERT, QB365 will helps to get more marks in Exams
QB365 - Question Bank Software
CBSE 12th Standard Physics Subject Alternating Current Ncert Exemplar 3 Mark Questions 2021
12th Standard CBSE
-
Reg.No. :
Physics
-
A magnetic field of flux density 10 T acts normally to the coil 50 turns having 100 cm2 area.Find emf induced if the coil is removed from the magnetic field in 0.15 s.
(a) -
Calculate the value of capacity in picofarad, which will make 101.4\(\mu H\) inductance to oscillate with the frequency of 1MHz.
(a) -
A \(2㎌\) capacitor, \(100 \ \Omega \) resistor and 8 H inductor are connected in series with an AC source. What should be the frequency of source for which the current drawn in the circuit is maximum?
If peak value of emf of source is 200 V, find the maximum current, inductive reactance, capacitive reactance, total impedance, peak value of current in the circuit.(a) -
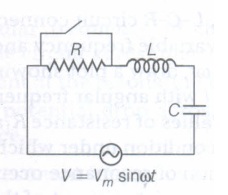
In the L-C-R circuit, shown in the figure, the AC driving voltage is V = Vm sin \(\omega\)t.
(i) Write down the equation of motion for q(t) .
(ii) At t = t0, the voltage source stops and R is short circuited. Now, write down how much energy is stored in each of L and C.
(iii) Describe subsequent motion of charges.
 (a)
(a) -
1 MW power is to be delivered from a power station to a town 10 km away. One uses a pair of Cu wires of radius 0.5 cm for this purpose. Calculate the fraction of ohmic losses to power transmitted, if
(i) power is ttansmitted at 220 V. Comment on the feasibility of doing this.
(ii) a step-up transformer is used to boost the. voltage at 11000 V, power transmitted, then a step-up transformer is used to bring voltage is 220 V.(Take, PCu = 1.7 x 10-8 SI unit)(a)
*****************************************
CBSE 12th Standard Physics Subject Alternating Current Ncert Exemplar 3 Mark Questions 2021 Answer Keys
-
Given, B = 10 T, N = 50 turns
A = 100 cm2 = 10-2 m2 , dt = 0.15 s
Magnetic flux link with the coil initially,
\(\phi \) = NBA =50 x 10 x 10-2 = 5Wb
But magnetic flux linked with the coil finally,i.e.,
(when removed from the magnetic field), \({ \phi }_{ 2 }\) = 0
Emf infuced, e = \(\frac { -d\phi }{ dt } =-(\frac { { \phi }_{ 2 }-{ \phi }_{ 1 } }{ dt } )\)
\(=-(\frac { 0-5 }{ 0.15 } )=33.33 \ v\) -
Given, inductance, L = 101.4\(\mu H\)
\(=101.4\times { 10 }^{ -6 }H\)
Frequency, v = 1MHz = 106Hz
Since, \(v=\frac { 1 }{ 2\pi \sqrt { LC } } \)
\(\Rightarrow \) \(C=\frac { 1 }{ 4{ \pi }^{ 2 }{ v }^{ 2 }L } \)
\(=\frac { 1\times 7\times 7 }{ 4\times 22\times 22\times { \left( { 10 }^{ 6 } \right) }^{ 2 }\times 101.4\times { 10 }^{ -6 } }\)
\(=2.496\times { 10 }^{ -10 }F\)
\(C=249.6 \ ㎊\) -
Given, capacitance, \(C=2㎌=2\times { 10 }^{ -6 }F\)
Resistance, R = 100\(\Omega\)
Inductance, L = 8H
Peak value of voltage, E0 = 200V
When frequency of AC source is equal to resonant frequency, then current drawn in the circuit is maximum.
\(\begin{aligned} \therefore \quad v & =v,=\frac{1}{2 \pi \sqrt{L C}} \\ \end{aligned}\)
\(\begin{aligned} & =\frac{1}{2 \times 3.14 \times \sqrt{8 \times 2 \times 10^{-6}}} \\ \end{aligned}\)
\(\begin{aligned} =\frac{1000}{8 \times 3.14}=39.8 \mathrm{~Hz} \end{aligned}\)
Peak value of current,
\(\begin{aligned} I_0 & =\frac{E_0}{R}=\frac{200}{100}=2 \mathrm{~A} \\ \end{aligned}\)
\(\begin{aligned} \because \quad X_C & =X_L=\omega L=2 \pi v L \\ \end{aligned}\)
\(\begin{aligned} & =2 \times 3.14 \times 39.8 \times 8=2000 \mathrm{~W} \end{aligned}\)
\(\begin{aligned} \Rightarrow \quad Z & =R=100 \Omega \end{aligned}\)
The voltages across inductor and resistor differ in phase by 90° and the voltages across inductor and capacitor differ in phase by 180°. -
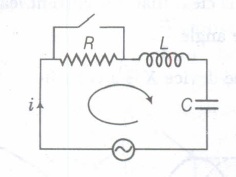
(i) Consider the R-L-C circuit as shown in the figure.
Given, V = Vmsin \(\omega\)t
Let current at any instant be i.
Note We have to apply KVL, write the equations in the form of current and charge, double differentiate the equation with respect to time and find the required relations.
Applying KVL in the given circuit,
\(i R+L \frac{d i}{d t}+\frac{q}{C}-V_{m} \sin \omega t=0\) ..........(i)
Now, we can write, \(i=\frac{d q}{d t} \Rightarrow \frac{d i}{d t}=\frac{d^{2} q}{d t^{2}}\)
From Eq. (i), we get
\(\frac{d q}{d t} R+L \frac{d^{2} q}{d t^{2}}+\frac{q}{C}=V_{m} \sin \omega t\)
\(\Rightarrow \quad L \frac{d^{2} q}{d t^{2}}+R \frac{d q}{d t}+\frac{q}{C}=V_{m} \sin \omega t\)
This is-the required equation of variation motion of charge.
(ii) Let \(q=q_{m} \sin (\omega t+\phi)=-q_{m} \cos (\omega t+\phi)\)
\(i=i_{m} \sin (\omega t+\phi)=q_{m} \omega \sin (\omega t+\phi)\)
\(i_{m}=\frac{V_{m}}{Z}=\frac{V_{m}}{\sqrt{R^{2}+\left(X_{C}-X_{L}\right)^{2}}}\)
and \(\phi=\tan ^{-1}\left(\frac{X_{C}-X_{L}}{R}\right)\)
When R is short circuited at t = to energy is stored in Land C.
\(U_{L}=\frac{1}{2} L i^{2}=\frac{1}{2} L\left[\frac{V_{m}}{\sqrt{R^{2}+\left(X_{C}-X_{L}\right)^{2}}}\right]^{2} \sin ^{2}(\omega t+\phi)\)
\(\text { and } U_{C}=\frac{1}{2} \times \frac{q^{2}}{C}=\frac{1}{2 C} \times\left(\frac{i_{m}}{\omega}\right)^{2} \cos ^{2}\left(\omega t_{0}+\phi\right)\)
\(=\frac{i_{m}^{2}}{2 C \omega^{2}} \cos ^{2}\left(\omega t_{0}+\phi\right) \quad\left[\because i_{m}=q_{m} \omega\right]\)
\(=\frac{1}{2 C}\left[\frac{V_{m}}{\sqrt{R^{2}+\left(X_{C}-X_{L}\right)^{2}}}\right]^{2} \frac{\cos ^{2}\left(\omega t_{0}+\phi\right)}{\omega^{2}}\)
\(=\frac{1}{2 C \omega^{2}}\left[\frac{V_{m}}{\sqrt{R^{2}+\left(X_{C}-X_{L}\right)^{2}}}\right]^{2} \cos ^{2}\left(\omega t_{0}+\phi\right)\)
(iii) When R is short circuited, it becomes an L - C oscillator. The capacitor will go on discharging and all energy will go to L.
Hence, there is an oscillation of energy from electrostatic to magnetic and again to electrostatic. -
(i) The town is 10 km away, length of pair of Cu wires
used, I = 20 km = 20000 m.
Resistance of Cu wires,
\(R=\rho \frac{l}{A}=\rho \frac{l}{\pi(r)^{2}}=\frac{1.7 \times 10^{-8} \times 20000}{3.14\left(0.5 \times 10^{-2}\right)^{2}} \approx 4 \Omega\)
\(I \text { at } 220 \mathrm{~V}, V I=10^{6} \mathrm{~W} ; I=\frac{10^{6}}{220}=0.45 \times 10^{4} \mathrm{~A}\)
RI2 = power loss = 4 x (0.45)2 x 108> 106 W
Therefore, this method cannot be used for transmission.
(ii) When power, P = 106 W is transmitted at 11000 V.
V \('I'\)= 106 W = 11000 \(I'\)
Current drawn, \(I^{\prime}=\frac{1}{1.1} \times 10^{2}\)
Power loss \(=R I^{2}=\frac{1}{121} \times 4 \times 10^{6}=3.3 \times 10^{4} \mathrm{~W}\)
\(\therefore\) Fraction of power loss \(=\frac{3.3 \times 10^{4}}{10^{6}}=3.3 \%\)






































