CBSE 12th Standard Physics Subject Atoms 3 Mark Ncert Exemplar Questions 2021
By QB365 on 24 May, 2021
QB365 Provides the updated NCERT Exemplar Questions for Class 12, and also provide the detail solution for each and every case study questions. NCERT Exemplar questions are latest updated question pattern from NCERT, QB365 will helps to get more marks in Exams
QB365 - Question Bank Software
CBSE 12th Standard Physics Subject Atoms 3 Mark Ncert Exemplar Questions 2021
12th Standard CBSE
-
Reg.No. :
Physics
-
assume that there is no repulsive force between the electrons in an atom but the force between positive and negative charges is given by Coulomb's law as usual.Under such circumstances, calculate the ground state energy of a He-atom.
(a) -
(i) The radius of the innermost electron orbit of a hydrogen atom is \({ r }_{ 1 }=5.3\times 10^{ -11 }\) Calculate its radius in n=2 orbit.
(ii) The total energy of an electron in the second excited state of the hydrogen atom is -1.51eV. Find out its
(a) kinetic energy and
(b) potential energy in this state(a) -
Consider a radioactive nucleus A which decays to a stable nucleus C through the following sequence:
A \(\longrightarrow \) B \(\longrightarrow \) C
where, B is an intermediate nuclei, which is also radioactive. Considering that there are N0 atoms of A initially, plot the graph showing the variation of number of atoms of A and B versus time.(a) -
A 12.5eV electron beam is used to bombard f = gaseous hydrogen at room temperature. Upto which energy level the H-atoms would be excited? Calculate the wavelengths of the first member of Lyman and first member of Balmer series.
(a) -
The deuteron id bound by nuclear forces just as H-atom is made up of p and e bound by electrostatic forces. If we consider the force between neutron and proton in deuteron as given in the form a coulomb potential but with an effective charge' F=\(\frac { 1 }{ { 4\pi \varepsilon }_{ 0 } } .\frac { { e }^{ '2 } }{ r } .\) Estimate the value of (e' /e) given that the binding energy of a deuteron is 2.2MeV.
(a)
*****************************************
CBSE 12th Standard Physics Subject Atoms 3 Mark Ncert Exemplar Questions 2021 Answer Keys
-
In He atom two electrons of charge (-2e) revolve around the nucleus.
And \(E_n=-{me^2Z^2\over8\epsilon_0^2n^2h^2}=4E\ \ \ [Z=2^2=4]\)
Ground state energy
= 4 x E = 4 x (-13.6) = -54.4eV -
Given, Bohr's radius, \({ r }_{ 1 }=5.3\times 10^{ -11 }\)
We know that, \({ r }_{ n }=n^{ 2 }{ r }_{ 1 }\)
Let be radius of the orbit for n = 2
Therefore, \(r_{ 2 }=(2)^{ 2 }\times 5.3\times 10^{ -11 }\quad =2.12\times 10^{ -10 }m\)
(ii) Given, total energy of an electron in second excited state,
E = 1.51 eV
(a) Kinetic energy of electron is equal to negative of the total energy
\(\Rightarrow \) K = -E = -(-1.51) = 1.51 eV
(b) Potential energy of electron is equal to negative of twice of its kinetic energy
\(\Rightarrow \) U = -2K = -2 x 1.51 = -3.02 eV -
By considering the situation given in the question,
At t = 0, NA = N0 (maximum), while NB = 0. As time increases, NA decreases exponentially and the number of atoms of B increases. They become (NB) maximum and finally drop to zero exponentially by radioactive decay law. So, graph showing the variation of number of atoms of A and B will be shown as below:
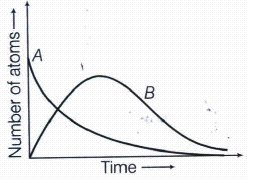
-
The energy of the gaseous hydrogen at room temperature are as given below:
E1 = -13.6eV, E = -3.4eV
E3 = -1.51eV, E4 = - 0.85eV
E3 - E1 = - 1.51 - ( - 13.6) = 12.09eV
and E4 - E1 = - 0.85 - ( - 13.6) = 12.75eV
As, both the values do not match the given value, but it is nearest to E4 - E1. Upto E4 - E1 energy level, the H-atoms would be excited.
Lyman series, \(\cfrac { 1 }{ \lambda } =R\left[ \cfrac { 1 }{ { 1 }^{ 2 } } -\cfrac { 1 }{ { n }^{ 2 } } \right] \)
For first member, n = 2
\(\therefore \) \(\cfrac { 1 }{ { \lambda }_{ 1 } } =R\left[ \cfrac { 1 }{ { 1 }^{ 2 } } -\cfrac { 1 }{ { 2 }^{ 2 } } \right] =1.097\times { 10 }\left[ \cfrac { 4-1 }{ 4 } \right] \)
\(\Rightarrow \) \({ \lambda }_{ 1 }=1.215\times { 10 }^{ -7 }m\)
Balmer series, \(\cfrac { 1 }{ \lambda } =R\left[ \cfrac { 1 }{ { 2 }^{ 2 } } -\cfrac { 1 }{ { n }^{ 2 } } \right] \)
For first member, n = 3
\(\therefore \) \(\cfrac { 1 }{ { \lambda }_{ 1 } } =R\left[ \cfrac { 1 }{ { 2 }^{ 2 } } -\cfrac { 1 }{ { 3 }^{ 2 } } \right] =1.097\times { 10 }\left[ \cfrac { 1 }{ 4 } -\cfrac { 1 }{ 9 } \right] \)
\(\Rightarrow \) \({ \lambda }_{ 1 }=6.56\times { 10 }^{ -7 }m\) -
The binding energy is H-atom,
\(E=\frac { { me }^{ 4 } }{ { \pi \varepsilon }_{ 0 }^{ 2 }{ h }^{ 2 } } =13.6 \ eV\quad ........(i)\)
If proton and neutron had charge e' each and were governed by the same electrostatic force, then in the above equation we would need to replace electronic mass m by the reduced mass m' of proton-neutron and the electronic charge e by e' .
\({ m }^{ ' }=\frac { M\times N }{ M+N } =\frac { M }{ 2 } \)
\( =\frac { 1836 \ m }{ 2 } =918 \ m\)
Here, M represents mass of a neutron/proton.
\(\therefore\) Binding energy \(=\frac { 918m{ \left( { e }^{ ' } \right) }^{ 4 } }{ { 8\varepsilon }_{ 0 }^{ 2 }{ h }^{ 2 } } =2.2\) MeV
Dividing Eqs. (ii) and (i), we get
\(918{ \left( \frac { { e }^{ ' } }{ e } \right) }^{ 4 }=\frac { 2.2 \ MeV }{ 13.6 \ eV }\)
\(=\frac { 2.2\times { 10 }^{ 6 } }{ 13.6 } \)
\( { \left( \frac { { e }^{ ' } }{ e } \right) }^{ 4 }=\frac { 2.2\times { 10 }^{ 6 } }{ 13.6\times 918 } =176.21\)
\( \left( \frac { { e }^{ ' } }{ e } \right) ={ \left( 176.21 \right) }^{ 1/4 }\)
\( =3.64\)






































