CBSE 12th Standard Physics Subject Dual Nature of Radiation and Matter HOT Questions 2 Mark Questions 2021
By QB365 on 27 May, 2021
QB365 Provides the HOT Question Papers for Class 12 Physics, and also provide the detail solution for each and every HOT Questions. HOT Questions will help to get more idea about question pattern in every exams and also will help to get more marks in Exams
QB365 - Question Bank Software
CBSE 12th Standard Physics Subject Dual Nature of Radiation and Matter HOT Questions 2 Mark Questions 2021
12th Standard CBSE
-
Reg.No. :
Physics
-
A proton and an \(\alpha \) particle are accelerated through the same potential. Which one of the two has
(i) greater value of de-Broglie wavelength associated with it and
(ii) less kinetic energy? Give reasons to justify your answer.(a) -
Find the ratio of the de-Broglie wavelength associated with protons accelerated through a potential of 128 V and a particles accelerated through a potential of 64 V.
To calculate the ratio of de-Baroglie wavelength of two particle find the ratio in terms of symbols and then put the given numerical values.(a) -
What is the
(i) momentum
(ii) speed
(iii) de-Broglie wavelength of an electron with kinetic energy of 120 eV?(a) -
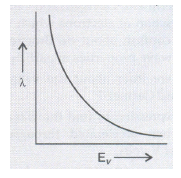
X-rays fall on a photosensitive surface to cause photoelectric emission. Assuming that the work function of the surface can be neglected, find the relation between the de-Broglie wavelength (\(\lambda \)) of the electrons emitted to the energy (Ev) of the incident photons. Draw the nature of the graph for Aas a function of Ev.
(a)
*****************************************
CBSE 12th Standard Physics Subject Dual Nature of Radiation and Matter HOT Questions 2 Mark Questions 2021 Answer Keys
-
(i) The de-Broglie wavelength of a particle is given as
\(\lambda=\frac{b}{\sqrt{2 m V_0 q}}\)
Since, \(\alpha\)-particle and proton both are accelerated through the same potential V0.
\(\begin{aligned} \therefore \quad \lambda \propto \frac{1}{\sqrt{m q}} \end{aligned}\)
\(\begin{aligned} \text { or } \quad \frac{\lambda_a}{\lambda_p}=\sqrt{\frac{m_p q_p}{m_a q_a}} \end{aligned}\)
As, charge on \(\alpha\)-particle = 2 \(\times\)charge on proton
\(q_{\mathrm{\alpha}}=2 q_{p} \Rightarrow \frac{q_{\mathrm{p}}}{q_{\mathrm{\alpha}}}=\frac{1}{2}\)
Mass of \(\alpha\)-particle = 4 \(\times\) Mass of proton
ma = 4 \(\times\) mp
\(\Rightarrow \quad \frac{m_p}{m_\alpha}=\frac{1}{4}\)
\(\begin{array}{ll} \therefore & \frac{\lambda_{\mathrm{a}}}{\lambda_p}=\sqrt{\frac{1}{4} \cdot \frac{1}{2}}=\frac{1}{2 \sqrt{2}}\end{array}\)
\(\begin{array}{ll} \Rightarrow & \lambda_p=2 \sqrt{2 \lambda_\alpha} \end{array}\)
i.e. proton has greater de-Broglie wavelength than that \(\alpha\)-paricle.
(ii) \(\mathrm{KE} \propto q\) (for same accelerating potential)
Since, charge on an \(\alpha\)-paricle is more as compared to a proton, so it will have a greater value of KE. Hence, proton will have lesser KE. -
de-Broglie wavelength is given by
\(\lambda =\frac { h }{ \sqrt { 2mK } } =\frac { h }{ \sqrt { 2mqV } }\)
\(\lambda \propto \frac { 1 }{ \sqrt { mqV } } \)
m = mass of charge particle, q = charge and V = potential difference
Raio of de-Broglie wavelengths of proton and a-particle is given by
\(\frac { \lambda _{ \alpha } }{ \lambda _{ p } } =\sqrt { \frac { m_{ \alpha }q_{ \alpha }V_{ \alpha } }{ m_{ p }q_{ p }V_{ p } } } =\sqrt { \left( \frac { m_{ \alpha } }{ m_{ p } } \right) \left( \frac { q_{ \alpha } }{ q_{ p } } \right) \left( \frac { V_{ \alpha } }{ V_{ p } } \right) } \)
\(\frac { m_{ \alpha } }{ m_{ p } } =4,\frac { q_{ \alpha } }{ q_{ p } } =2,\frac { V_{ \alpha } }{ V_{ p } } =\frac { 1 }{ 2 } \)
a-particle is 4 toimes heavier than proton and it has double the charge than that of proton
\(\frac { \lambda _{ p } }{ \lambda _{ \alpha } } =\sqrt { 4\times 2\times \frac { 1 }{ 2 } } =2\quad \Rightarrow \lambda _{ p }:\lambda _{ \alpha }=2:1\) -
Given, Kinetic energy = KE = 120 eV
p=\(\sqrt { 2eVm } =\sqrt {2KE.m }\) \([\because K E=e V]\)
\(P=\sqrt { 2\times 120\times 1.6\times 10^{ -19 }\times 9.1\times 10^{ -31 } } \)
\(=5.91\times 10^{ -24 }\ kg-m/s\)
(ii) We know that momentum, p = mv
or, \(v=\frac{p}{m}=\frac{5.91 \times 10^{-24}}{9.1 \times 10^{-31}}\)
\(=6.5 \times 10^{6} \mathrm{~m} / \mathrm{s}\)
(iii) de-Broglie wavelength associated with electron,
\(\lambda =\frac { 12.27 }{ \sqrt { V_{ } } } \mathring { A } =\frac { 12.27 }{ \sqrt { 120 } } \mathring { A=0.112\times 10^{ -9 } } \ m=0.112 \ nm\) -
\( { E }_{ v }={ \phi }_{ 0 }+{ K }_{ max }\)
\( \Rightarrow { \phi }_{ 0 }=0\)
\( \Rightarrow \ { E }_{ v }={ K }_{ max }\)
\(\Rightarrow { K }_{ max }=\frac { { p }^{ 2 } }{ 2m } ={ E }_{ v }\)
\( \Rightarrow \ p=\sqrt { 2m{ E }_{ v } } \)
Wavelength \(\left( \lambda \right) \) of emitted electrons,
\(\lambda =\frac { h }{ p } =\frac { h }{ \sqrt { 2m{ E }_{ v } } } \)