CBSE 12th Standard Physics Subject Dual Nature of Radiation and Matter Ncert Exemplar 3 Mark Questions 2021
By QB365 on 24 May, 2021
QB365 Provides the updated NCERT Exemplar Questions for Class 12, and also provide the detail solution for each and every case study questions. NCERT Exemplar questions are latest updated question pattern from NCERT, QB365 will helps to get more marks in Exams
QB365 - Question Bank Software
CBSE 12th Standard Physics Subject Dual Nature of Radiation and Matter Ncert Exemplar 3 Mark Questions 2021
12th Standard CBSE
-
Reg.No. :
Physics
-
If h is Planck's constant, find the momentum of a wavelength 0.4\(\mathring { A } \)
(a) -
An electron, \(\alpha \) -particle and a proton have the same de-Broglie wavelengths. Which of
theseparticle has
(i) minimum kinetic energy?
(ii) maximum kinetic energy and why?
In what way has the wave nature of electron beam exploited in an electron microscope?(a) -
(i) Write the important properties of photons which are used to establish Einstein's photoelectric equation.
(ii) Use this equation to explain the concept of
(a) threshold frequency and
(b) stopping potential.(a) -
A student performs an experiment on photoelectric effect, using two materials A and B. A plot of Vstop versus v is given in the figure.
(i) Which material A or B has a higher work function?
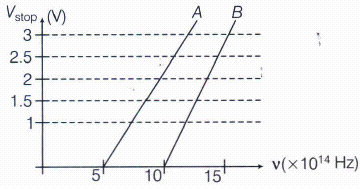
(ii) Given the electric charge of an electron =\(1.6\times { 10 }^{ -19 }C\), find the value of h obtained from the experiment for both A and B.
Comment on whether it is consistent with the Einstein's theory.(a) -
A proton and an electron have same de-Broglie Wavelength. Which of them moves fast and which possesses more kinetic energy? Justify your answer.
(a)
*****************************************
CBSE 12th Standard Physics Subject Dual Nature of Radiation and Matter Ncert Exemplar 3 Mark Questions 2021 Answer Keys
-
Since, \(p=\frac { h }{ \lambda } \)
Given, \(\lambda =0.4\mathring { A } =0.4\times 10^{ -10 }m\)
\(h=6.6\times { 10 }^{ -34 } \ J-s\)
\( \therefore \ p=\frac { 6.6\times { 10 }^{ -34 } }{ 0.4\times 10^{ -10 } } \)
\(\Rightarrow \ p=16.5\times { 10 }^{ -24 }\ kg-ms^{ -1 }\) -
de-Broglie matter wave equation,
\(\lambda =\frac { h }{ p } =\frac { h }{ \sqrt { 2mK } } \ \left[ \because K=\frac { { P }^{ 2 } }{ 2m } \right] \)
where K is kinetic energy and m is a mass of the particle.
\(K=\frac { { h }^{ 2 } }{ 2m{ \lambda }^{ 2 } } \) [ for same wavelength \( \lambda] \)
\(K\propto \frac { 1 }{ m }\)
\(\Rightarrow \ { K }_{ e }:{ K }_{ \alpha }:{ K }_{ p }=\frac { 1 }{ { m }_{ e } } :\frac { 1 }{ { m }_{ \alpha } } :\frac { 1 }{ { m }_{ p } } \)
where \({ m }_{ e },{ m }_{ p } \ and \ { m }_{ \alpha }\) are masses of electron, proton and \(\alpha \) -particle, respectively.
Also, \({ K }_{ e },k_{ p } \ and \ K_{ \alpha }\) are their respective kinetic energies.
\(\because \ m_{ \alpha }>m_{ p }>m_{ e }\)
\(\\ \Rightarrow m_{ \alpha }m_{ p }>m_{ e }m_{ \alpha }>m_{ e }m_{ p }\)
\(\\ { K }_{ e }>k_{ p }>K_{ \alpha }\)
(i) \(\alpha \) particle possess minimum kinetic energy
(ii) The electron has maximum kinetic energy. The magnifying power of an electron microscope is inversely related to the wavelength of radiation used. The Smaller wavelength of the electron beam in comparison to visible light increases the magnifying power of the microscope. -
(i) Important properties of photons which are used to establish Einstein's photoelectric equations are as follows:
(a) In interaction of radiation with matter, radition behaves as, if it is make up of particles called photons.
(b) All photons of light of a particular frequency v or wavelength \(\lambda \) have the same energy \(E(=hv=\frac { hc }{ \lambda } )\) and \(P(=\frac { hv }{ c } =\frac { h }{ \lambda } )\)
Whatever the indensity of radiation may be.
(ii) Since, Einstein's photoelectric equation is given by
\({ KE }_{ max }=\frac { 1 }{ 2 } { mv }^{ 2 }_{ max }=hv=h{ v }_{ 0 } =e{ V }_{ 0 }\)
(a) For a given material, there exist a certain minimum frequency of the incident radition, below which no emission of photoelectron takes place. This frequency is called threshold frequency (V0). Above threshold frequency, the maximum kinetic energy of the emitted photoelectron or equivalent stopping potential is independent of the intensity of the incident light but depends only upon the frequency of the incident light.
(b) If the collecting plate in the photoelectric apparatus is made at high negative potenrial, then most of the high energetic electrons get repelled back along the same path and the photoelectric current in the circuit becomes zero. So, for a particular frequency of incident radiation, the minimum negative potential for which the electric current becomes zero is called cut-off or stopping potential(V0). -
Given, thershold frequency of A is
\({ v }_{ OA }=5\times { 1 }0^{ 14 }\quad Hz\)
and thershold frequency of B is \({ v }_{ OB }=10\times { 1 }0^{ 14 }\quad Hz\)
We know that work function,
\({ \phi }_{ 0 }=h{ v }_{ 0 } \ or \ { \phi }_{ 0 }\propto { v }_{ 0 }\)
\(So,\ \frac { { \phi }_{ OA } }{ { \phi }_{ OB } } =\frac { 5\times { 10 }^{ 14 } }{ 10\times { 10 }^{ 14 } } <1 \ \Rightarrow { \phi }_{ OA }<{ \phi }_{ OB }\)
Thus, work function of B is higher than A.
(ii) For metal A, slope
\(=\frac { h }{ e } =\frac { 2 }{ (10-5)\times { 10 }^{ 14 } } \)
\(or \ h=\ \frac { 2\times e }{ 5\times { 10 }^{ 14 } } =\frac { 2\times 1.6\times { 10 }^{ -19 } }{ 5\times { 10 }^{ 14 } } \)
\(=6.4\times { 10 }^{ -34 }\ J-s\)
For metal B, slope \(=\frac { h }{ e } =\frac { 2.5 }{ (15-10)\times { 10 }^{ 14 } } \)
\(\\ or\quad h=\frac { 2.5\times e }{ 5\times { 10 }^{ 14 } } =\frac { 2.5\times 1.6\times { 10 }^{ -19 } }{ 5\times { 10 }^{ 14 } } =8\times { 10 }^{ -34 }J-s\)
Since, the value of b from experiment for metals A and B is different. Hence, experiment is not consistent with theory. -
Kinetic energy of particle of mass m having momentum p is given by
\(k=\frac { p^{ 2 } }{ 2m } \quad p=\sqrt { 2mK } \)
The de-Broglie wavelength \(\lambda =\frac { h }{ p } =\frac { h }{ \sqrt { 2mK } }\)
\( \\ p=\frac { h }{ \lambda } \)
\(\\ K=\frac { h^{ 2 } }{ 2m\lambda ^{ 2 } } \)
If \(\lambda \) is constant then from Eq (i) we get
p = constant,i.e mpvp = meve
\(\text { or } \frac{v_{p}}{v_{e}}=\frac{m_{e}}{m_{p}}<1\)
or vp < ve
If \(\lambda \) is constant then from (ii) \(K \propto \frac{1}{m}\)
\((\therefore \frac{K_{p}}{K_{e}}=\frac{m_{e}}{m_{p}}<1 \text { or } K_{p})\)
It means that the velocity of electron is greater than that of proton. Kinetic energy of electron is greater than that of proton.






































