CBSE 12th Standard Physics Subject Electrostatic Potential And Capacitance Chapter Case Study Questions 2021
By QB365 on 21 May, 2021
QB365 Provides the updated CASE Study Questions for Class 12 , and also provide the detail solution for each and every case study questions . Case study questions are latest updated question pattern from NCERT, QB365 will helps to get more marks in Exams
QB365 - Question Bank Software
CBSE 12th Standard Physics Subject Electrostatic Potential And Capacitance Case Study Questions 2021
12th Standard CBSE
-
Reg.No. :
Physics
-
The potential at any observation point P of a static electric field is defined as the work done by the external agent (or negative of work done by electrostatic field) in slowly bringing a unit positive point charge from infinity to the observation point. Figure shows the potential variation along the line of charges. Two point charges Q1 and Q2 lie along a line at a distance from each other.
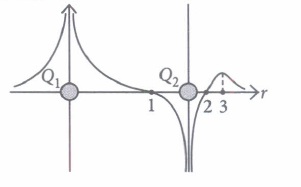
(i) At which of the points 1, 2 and 3 is the electric field is zero?(a) 1 (b) 2 (c) 3 (d) Both (a) and (b) (ii) The signs of charges Q1 and Q2 respectively are
(a) positive and negative (b) negative and positive (c) positive and positive (d) negative and negative
(iii) Which of the two charges Q1 and Q2 is greater in magnitude?(a) Q2 (b) Q1 (c) Same (d) Can't determined (iv) Which of the following statement is not true?
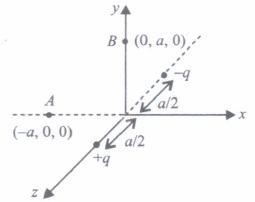
(a) Electrostatic force is a conservative force (b) Potential energy of charge q at a point is the work done per unit charge in bringing a charge from any point to infinity (c) When two like charges lie infinite distance apart, their potential energy is zero. (d) Both (a) and (c). (v) Positive and negative point charges of equal magnitude are kept at \(\left(0,0, \frac{a}{2}\right)\) and \(\left(0,0, \frac{-a}{2}\right)\) respectively.
The work done by the electric field when another positive point charge is moved from (-a, 0, 0) to (0, a, 0) is(a) positive (b) negative (c) zero (d) depends on the path connecting the initial and final positions (a) -
For the various charge systems, we represent equipotential surfaces by curves and line of force by full line curves. Between any two adjacent equipotential surfaces, we assume a constant potential difference the equipotential surfaces of a single point charge are concentric spherical shells with their centres at the point charge. As the lines of force point radially outwards, so they are perpendicular to the equipotential surfaces at all points.
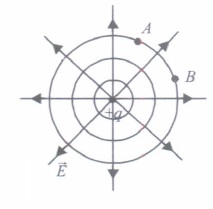
(i) Identify the wrong statement.(a) Equipotential surface due to a single point charge is spherical. (b) Equipotential surface can be constructed for dipoles too. (c) The electric field is normal to the equipotential surface through the point. (d) The work done to move a test charge on the equipotential surface is positive (ii) Nature of equipotential surface for a point charge is
(a) Ellipsoid with charge at foci (b) Sphere with charge at the centre of the sphere (c) Sphere with charge on the surface of the sphere (d) Plane with charge on the surface (iii) A spherical equipotential surface is not possible
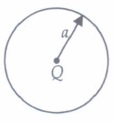
(a) inside a uniformly charged sphere (b) for a dipole (c) inside a spherical condenser (d) for a point charge (iv) The work done in carrying a charge q once round a circle of radius a with a charge Q at its centre is
\(\text { (a) } \frac{q Q}{4 \pi \varepsilon_{0} a}\) \(\text { (b) } \frac{q Q}{4 \pi \varepsilon_{0} a^{2}}\) \(\text { (c) } \frac{q}{4 \pi \varepsilon_{0} a}\)
(d) zero
(v) The work done to move a unit charge along an equipotential surface from P to Q
(a) must be defined as \(-\int_{P}^{Q} \vec{E} \cdot d \vec{l}\) (b) is zero (c) can have a non-zero value (d) both (a) and (b) are correct (a) -
The electrical capacitance of a conductor is the measure of its ability to hold electric charge. An isolated spherical conductor of radius R. The charge Q is uniformly distributed over its entire surface. It can be assumed to be concentrated at the centre of the sphere. The potential atany point on the surface of the spherical conductor will be \(V=\frac{1}{4 \pi \varepsilon_{0}} \frac{Q}{R}\).
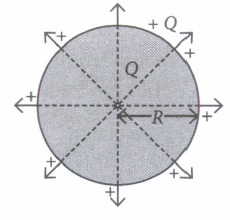
Capacitance of the spherical conductor situated in vacuum is \(C=\frac{Q}{V}=\frac{Q}{\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{Q}{R}} \text { or } C=4 \pi \varepsilon_{0} R\) Clearly, the capacitance of a spherical conductor is proportional to its radius.
The radius of the spherical conductor of 1F capacitance is R = \(\frac{1}{4 \pi \varepsilon_{0}}\). C and this radius is about 1500 times the radius of the earth \(\left(\sim 6 \times 10^{3} \mathrm{~km}\right)\).
(i) If an isolated sphere has a capacitance 50pF. Then radius is(a) 90 ern (b) 45 cm (c) 45 m (d) 90 m (ii) How much charge should be placed on a capacitance of 25 pF to raise its potential to l05 V?
\(\text { (a) } 1 \mu \mathrm{C}\) \(\text { (b) } 1.5 \mu \mathrm{C}\) \(\text { (c) } 2 \mu \mathrm{C}\) \(\text { (d) } 2.5 \mu \mathrm{C}\) (iii) Dimensions of capacitance is
\(\text { (a) }\left[M L^{-2} T^{4} A^{2}\right]\) \(\text { (b) }\left[\mathrm{M}^{-1} \mathrm{~L}^{-1} \mathrm{~T}^{3} \mathrm{~A}^{1}\right]\) \(\text { (c) }\left[\mathrm{M}^{-} \mathrm{L}^{-2} \mathrm{~T}^{4} \mathrm{~A}^{2}\right]\) \(\text { (d) }\left[M^{0} L^{-2} T^{4} A^{1}\right]\) (iv) Metallic sphere of radius R is charged to potential V. Then charge q is proportional to
(a) V (b) R (c) both V and R (d) none of these. (v) If 64 identical spheres of charge q and capacitance C each are combined to form a large sphere. The charge and capacitance of the large sphere is
(a) 64q, C (b) 16q, 4C (c) 64q, 4C (d) 16q, 64C (a) -
A dielectric slab is a substance which does not allow the flow of charges through it but permits them to exert electrostatic forces on one another.
When a dielectric slab is placed between the plates, the field Eo polarises the dielectric. This induces charge -Qp on the upper surface and + Qp on the lower surface of the dielectric. These induced charges set up a field Ep inside the dielectric in the opposite direction of \(\vec{E}_{0}\) as shown.
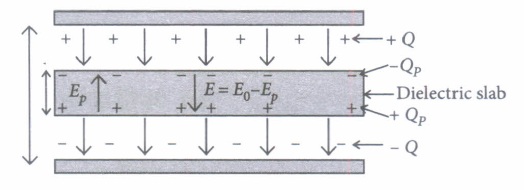
(I) In a parallel plate capacitor, the capacitance increases from \(4 \mu \mathrm{F}\) to 80\(\mu \mathrm{F}\) on introducing a dielectric medium between the plates. What is the dielectric constant of the medium?(a) 10 (b) 20 (c) 50 (d) 100 (ii) A parallel plate capacitor with air between the plates has a capacitance of 8 pF. The separation between the plates is now reduced half and the space between them is filled with a medium of dielectric constant 5.
Calculate the value of capacitance of the capacitor in second case.(a) 8pF (b) 10pF (c) 80pF (d) 100pF (iii) A dielectric introduced between the plates of a parallel plate condenser
(a) decreases the electric field between the plates (b) increases the capacity of the condenser (c) increases the charge stored in the condenser (d) increases the capacity of the condenser (iv) A parallel plate capacitor of capacitance 1 pF has separation between the plates is d. When the distance of separation becomes 2d and wax of dielectric constant x is inserted in it the capacitance becomes 2 pF. What is the value of x?
(a) 2 (b) 4 (c) 6 (d) 8 (v) A parallel plate capacitor having area A and separated by distance d is filled by copper plate of thickness b. The new capacity is
\(\text { (a) } \frac{\varepsilon_{0} A}{d+\frac{b}{2}}\) \(\text { (b) } \frac{\varepsilon_{0} A}{2 d}\) \(\text { (c) } \frac{\varepsilon_{0} A}{d-b}\) \(\text { (d) } \frac{2 \varepsilon_{0} A}{d+\frac{b}{2}}\) (a) -
When an insulator is placed in an external field, the dipoles become aligned. Induced surface charges on the insulator establish a polarization field \(\vec{E}_{i}\) in its interior. The net field \(\vec{E}\) in the insulator is the vector sum of \(\vec{E}_{0}\) and \(\vec{E}_{i}\) as shown in the figure.

On the application of external electric field, the effect of aligning the electric dipoles in the insulator is called polarisation and the field \(\vec{E}_{i}\) is known as the polarisation field.
The dipole moment per unit volume of the dielectric is known as polarisation \((\vec{P})\).
For linear isotropic dielectrics, \(\vec{P}=\chi \vec{E}\) where X = electrical susceptibility of the dielectric medium.
(i) Which among the following is an example of polar molecule?(a) O2 (b) H2 (c) N2 (d) HCl (ii) When air is replaced by a dielectric medium of constant K, the maximum force of attraction between two charges separated by a distance
(a) increases K times (b) remains unchanged (c) decreases Ktimes (d) increases 2K times (iii) Which of the following is a dielectric?
(a) Copper (b) Glass (c) Antimony (Sb) (d) None of these (iv) For a polar molecule, which of the following statements is true?
(a) The centre of gravity of electrons and protons coincide (b) The centre of gravity of electrons and protons do not coincide (c) The charge distribution is always symmetrical. (d) The dipole moment is always zero. (v) When a comb rubbed with dry hair attracts pieces of paper. This is because the
(a) comb polarizes the piece of paper (b) comb induces a net dipole moment opposite to the direction of field (c) electric field due to the comb is uniform (d) comb induces a net dipole moment perpendicular to the direction of field (a)
*****************************************
CBSE 12th Standard Physics Subject Electrostatic Potential And Capacitance Case Study Questions 2021 Answer Keys
-
(I) (c) : As \(\frac{-d V}{d r}=E_{r}\) the negative of the slope of V versus r curve represents the component of electric field along r. Slope of curve is zero only at point 3. Therefore, the electric field vector is zero at point 3.
(ii) (a) : Near positive charge, net potential is positive and near a negative charge, net potential is negative. Thus, charge Q1 is positive and Q2 is negative.
(iii) (b) : From the figure, it can be seen that net potential due to two charges is positive everywhere in the region left to charge Q1. Therefore the magnitude of potential due to charge Q1 is greater than due to Q2.
(iv) (b)
(v) (c) : It can be seen that potential at the points both A and B are zero. When the charge is moved from A to B, work done by the electric field on the charge will be zero.
-
(i) (d)
(ii) (b)
(iii) (b)
(iv) (d): The electrical potential at any (J) point on circle of radius a due to charge Qa Q.at Its centre I.S V = \(V=\frac{1}{4 \pi \varepsilon_{0}} \frac{Q}{a}\)
It is an equipotential surface.
Hence, work done in carrying a charge q round the circle is zero.
(v) (d): Work done to move a unit charge along an equipotential surface from P to Q,
\(W=-\int_{P}^{Q} \vec{E} \cdot d \vec{l}\)
On equipotential surface \(\vec{E} \perp d \vec{l}\)
\(W=-\int_{P}^{Q} E(d l) \cos 90^{\circ}=0\) -
(i) (b): Here \(C-50 p F-50 \times 10^{-12} F, V=10^{4} V\)
\(R=\frac{1}{4 \pi \varepsilon_{0}} \cdot C=9 \times 10^{9} \mathrm{mF}^{-1} \times 50 \times 10^{-12} \mathrm{~F}\)
= 45 x 10-2 m = 45 cm
(ii) (d): As \(q=C V=25 \times 10^{-12} \times 10^{5}=2.5 \mu \mathrm{C}\)
(iii) (c)
(iv) (c): As charge \(q=C V=\left(4 \pi \varepsilon_{0} R\right) V\)
\(\therefore\) q depends on both V and R.
(v) (c): 64 drops have formed a single mop of radius R. Volume oflarge sphere = 64 x Volume of small sphere
\(\therefore \frac{4}{3} \pi R^{3}=64 \frac{4}{3} \pi r^{3} \Rightarrow R=4 r \text { and } Q_{\text {total }}=64 q\)
\(C^{\prime}=4 \pi \varepsilon_{0} R \Rightarrow C^{\prime}=\left(4 \pi \varepsilon_{0}\right) \cdot 4 r \Rightarrow C^{\prime}=4 C\) -
(i) (b): \(k=\frac{\text { Capacitance with dielectric }}{\text { Capdcitance without dielectric }}\) \(=\frac{80 \mu \mathrm{F}}{4 \mu \mathrm{F}}=20\)
(ii) (c): Capacitance of the capacitor with air between plates
\(C^{\prime}=\frac{\varepsilon_{0} A}{d}=8 \mathrm{pF}\)
With the capacitor is filled with dielectric (k = 5) between its plates and the distance between the plates is reduced by half, capacitance become \(C=\frac{\varepsilon_{0} k A}{d / 2}=\frac{\varepsilon_{0} \times 5 \times A}{d / 2}=10 C^{\prime}=10 \times 8=80 \mathrm{pF}\)
(iii) (d): If a dielectric medium of dielectric constant K is filled completely between the plates then capacitance increases by K times .
(iv) (b): \(C=\frac{\varepsilon_{0} A}{d}=1 \mathrm{pF}\) ....(i)
\(C^{\prime}=\frac{x \varepsilon_{0} A}{(2 d)}=2 \mathrm{pF}\) ....(ii)
Divide (ii) by (i), x/2 = 2/1 \(\Rightarrow\) x = 4
(v) (c) : As capacitance \(C_{o}=\frac{\varepsilon_{o} A}{d}\)
\(\therefore\) After inserting copper plate, \(C=\frac{\varepsilon_{o} A}{d-b}\) -
(i) (d): In polar molecule the centres of positive and negative charges are separated even when there is no external field. Such molecule have a permanent dipole moment. Ionic molecule like HCl is an example of polar molecule.
(ii) (c): As, \(F_{m}=\frac{F_{o}}{K}\)
\(\therefore\) The maximum force decreases by K times.
(iii) (b)
(iv) (b): A polar molecule is one in which the centre of gravity for positive and negative charges are separated.
(v) (a)






































