(i) Given, C₁ = 1\(\mu F\)  C₂ = 2\(\mu F\) C₃ = 3\(\mu F\)
The combined capacity (C_s) in series combination is given by
 \(\frac { 1 }{ { C }_{ s } } =\frac { 1 }{ { C }_{ 1 } } +\frac { 1 }{ { C }_{ 2 } } +\frac { 1 }{ { C }_{ 3 } } =\frac { 1 }{ 1 } +\frac { 1 }{ 2 } +\frac { 1 }{ 3 } =\frac { 11 }{ 6 } \)
\(\Rightarrow { C }_{ s }=\frac { 6 }{ 11 } \mu F\)
The combined capacity (C_p) in parallel combination is given by 
C_p = C₁ + C₂ +C₃ = 1 + 2 + 3 = 6\(\mu F\) 
\(\Rightarrow { C }_{ p }=11{ C }_{ s }\) 
(ii)  As, \({ \ C }_{ p }>{ C }_{ s }\) 
\(\therefore \) The charge supplied by 100 V battery
\({ q }_{ p }={ C }_{ p }V=6\mu F\times 100=6\times { 10 }^{ -6 }\times 100\)   
\(\\ { q }_{ p }=6\times { 10 }^{ -4 }C\)​​​​= 600 \(\mu\)C

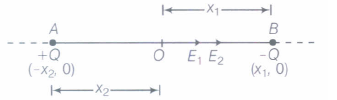
Electric field intensity at Point O due to + Q charge,
\({ E }_{ 1 }=\frac { 1 }{ 4\pi { \varepsilon }_{ o } } \times \frac { Q }{ { \left( { x }_{ 2 } \right) }^{ 2 } } (towards \ B) .....(i)\)
Electric field intensity at Point O due to - Q charge,
\({ E }_{ 2 }=\frac { 1 }{ 4\pi { \varepsilon }_{ o } } \times \frac { Q }{ { \left( { x }_{ 1 } \right) }^{ 2 } } (towards \ B).....(i)\)
\({ \because }\) E₁ and E₂ act along the same direction.
\({ \because }\) Net electric field intensity at point O,
\(E={ E }_{ 1 }+{ E }_{ 2 }=\frac { 1 }{ 4\pi { \varepsilon }_{ o } } \times \frac { Q }{ { \left( { x }_{ 2 } \right) }^{ 2 } } +\frac { 1 }{ 4\pi { \varepsilon }_{ o } } \times \frac { Q }{ { \left( { x }_{ 1 } \right) }^{ 2 } } (towards \ B)\)
\( E=\frac { Q }{ 4\pi { \varepsilon }_{ o } } \left[ \frac { 1 }{ { x }_{ 2 }^{ 2 } } +\frac { 1 }{ { x }_{ 1 }^{ 2 } } \right] \)

\(Here,q=1\times { 10 }^{ -6 }C,2a=2cm=0.02m\)
\(\therefore p=q\times 2a=(1\times { 10 }^{ -6 })\times 0.02=2\times { 10 }^{ -8 }cm\)
Intensity of the external electric field, E \(=1.0\times { 10 }^{ 5 }N/C\)
\((i){ \tau }_{ max }=pE=(2\times { 10 }^{ -8 })(1.0\times { 10 }^{ 5 })=2\times { 10 }^{ -3 }N-m\ (1)\)
(ii) Net work done in turning the dipole from \(\ 0^0\ to\ 180^0,\)
\( i.e \ W={ \int { _{ { 0 }^{ 0 } }^{ { 180 }^{ 0 } } } }\tau d\theta =\int { _{ { 0 }^{ 0 } }^{ { 180 }^{ 0 } } } pEsin\theta =pE{ [-cos\theta ] }_{ { 0 }^{ 0 } }^{ { 180 }^{ 0 } }\)
\(=-pE(cos{ 180 }^{ 0 }-cos{ 0 }^{ 0 })=2pE\)
\(=2\times (2\times { 10 }^{ -8 })(1\times { 10 }^{ 5 })J=4\times { 10 }^{ -3 }J\ (11/2)\)

Let q₁ and q₂ be the charges on them

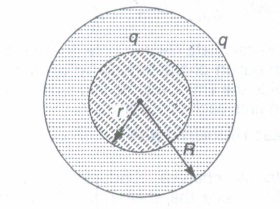
\(\sigma_1\) = \(\sigma_2\)
\(\therefore \ \frac{q_{1}}{4 \pi r^{2}}=\frac{q_{2}}{4 \pi R^{2}}\)
\(\therefore \ \frac{q_{1}}{q_{2}}=\frac{r^{2}}{R^{2}}\)
i.e. charge on them is distributed in above ratio or \(q_{1}=\frac{r^{2}}{r^{2}+R^{2}} Q \ \text { and } q_{2}=\frac{R^{2}}{r^{2}+R^{2}} Q\)
\(\therefore\) Potential at.centre 
V = Potential due to q₁ + Potential due to q ₂
\(\therefore \ V=\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{q_{1}}{r}+\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{q_{2}}{R}=\frac{Q(R+r)}{4 \pi \varepsilon_{0}\left(r^{2}+R^{2}\right)}\) 

(i) The total charge of the capacitor remains conserved on introduction of dielectric slab. Also, the capacitance of capacitor increases to K times of original values. 
\(\therefore \\ \)  CV = C' V '= (KC) V' \(\Rightarrow V'=\frac { V }{ K } \) 
\(\therefore \\ \) New electric field,
\(E'=\frac { V' }{ d } =\left( { \frac { { V }/{ K } }{ d } } \right) =\left( \frac { V }{ d } \right) \frac { 1 }{ k } =\frac { E }{ K } \) 
​​\(\therefore \\ \)  On introduction of dielectric medium, new electric field E' becomes \(\frac { 1 }{ K } \) times of its original value (decrease).
(ii) The thickness of dieletric slab is \(\frac{d}{2}, \text { i.e. } t=\frac{d}{2}\)
The capacitance of a capacitor due to dielectric slab,
\(\begin{aligned} C & =\frac{\varepsilon_0 A}{d-t+\frac{t}{K}} \end{aligned}\)
\(\begin{aligned} =\frac{\varepsilon_0 A}{d-\frac{d}{2}+\frac{d}{2 K}}=\frac{2 \varepsilon_0 A}{d\left(1+\frac{1}{K}\right)} \end{aligned}\)