CBSE 12th Standard Physics Subject Magnetism And Matter Ncert Exemplar 2 Mark Questions With Solutions 2021
By QB365 on 22 May, 2021
QB365 Provides the updated NCERT Exemplar Questions for Class 12, and also provide the detail solution for each and every case study questions. NCERT Exemplar questions are latest updated question pattern from NCERT, QB365 will helps to get more marks in Exams
QB365 - Question Bank Software
CBSE 12th Standard Physics Subject Magnetism And Matter Ncert Exemplar 2 Mark Questions With Solutions 2021
12th Standard CBSE
-
Reg.No. :
Physics
-
Consider the plane S formed by the dipole axis and the axis of the earth. Let P be point on the magnetic equator in S. Let Q be the point of intersection of the geographical and magnetic equators. Obtain the declination and dip angles at P and Q.
(a) -
From molecular view point, discuss the temperature dependence of susceptibility for diamagnetism, paramagnetism and ferromagnetism.
(a) -
A ball of superconducting matesial is dipped in liquid nitrogen and placed near a bar magnet.
(i) In which direction will it move?
(ii) What will be the direction of its magnetic moment?(a) -
Explain quantitatively the order of magnitude difference between the diamagnetic susceptibility of \(\mathrm{N}_{2}\left(\sim 5 \times 10^{-9}\right)\) (at STP) and \(\mathrm{Cu}\left(\sim 10^{-5}\right)\)
(a) -
A proton has spin and magnetic moment just like an electron. Why then its effect is neglected in magnetism of materials?
(a)
*****************************************
CBSE 12th Standard Physics Subject Magnetism And Matter Ncert Exemplar 2 Mark Questions With Solutions 2021 Answer Keys
-
P is in the plane of S, needle is in North, so the declination is zero.
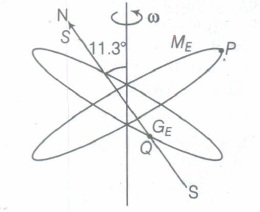
P is also on the magnetic equator, so the angle of dip is zero, because the value of angle of dip at equator is zero. Q is also on the magnetic equator, so the angle of dip is zero.
As, the earth is tilted on its axis by 113°, thus the declination at Q is 113°. -
Susceptibility of magnetic material \(\chi=\frac{I}{H}\) where I is the intensity of magnetisation induced in the material and H is the magnetising force.
Diamagnetism is due to orbital motion of electrons in an atom developing magnetic moments opposite to applied field. Thus, the resultant magnetic moment of the diamagnetic material is zero and hence, the susceptibility X of diamagnetic material is not much affected by temperature.
Paramagnetism and ferromagnetism is due to alignment of atomic magnetic moments in the direction of the applied field. As temperature is raised, the alignment is disturbed, resulting decrease in susceptibility of both with increase in temperature. -
Both a superconducting material and nitrogen are diamagnetic in nature. When a ball of superconducting material is dipped in liquid nitrogen, it behaves as a diamagnetic material. When placed near a bar magnet, it will be feebly magnetised opposite to the direction of magnetising field.
Because of this,
(i) it will be repelled (i.e. move away from magnet)
(ii) the direction of magnetic moment will be opposite to the direction of magnetic field of bar magnet. -
Here, \(\chi_{m\left(N_{2}\right)}=5 \times 10^{-9} \text {and } \chi_{m(\mathrm{Cu})}=10^{-5}\)
\(\therefore \quad \frac{\chi_{m\left(\mathrm{~N}_{2}\right)}}{\chi_{m(\mathrm{Cu})}}=\frac{5 \times 10^{-9}}{10^{-5}}=5 \times 10^{-4}\)
As, \(\chi_{m}=\frac{I}{H}=\frac{M / V}{H}=\frac{M}{H V}=\frac{M \rho}{H m}\)
where, M= magnetic moment
V = volume, m = mass and p = density
\(\therefore \quad \chi_{m} \propto \rho, \text { for given value of } \frac{M}{H m}\)
\(\text { Thus, } \frac{\chi_{m\left(N_{2}\right)}}{\chi_{m(C u)}}=\frac{P_{N_{2}}}{\rho_{C u}}=\frac{28 \mathrm{~g} / 22400 \mathrm{cc}}{8 \mathrm{~g} / \mathrm{cc}}=1.6 \times 10^{-4}\)
Hence, major difference is accounted for by density. -
As we know that, the magnetic moment of electron or proton is inversely proportional to the mass of electron or proton, respectively.
Magnetic. moment of electron, \(\mu_{e} \text { oc } \frac{1}{m_{e}}\)
where, me = mass of electron
Magnetic moment of proton, \(\mu_{p} \propto \frac{1}{m_{p}}\)
where, mp = mass of proton
\(\frac{\mu_{e}}{\mu_{p}}=\frac{m_{p}}{m_{e}}\) .......(i)
As, we know that, me < < mp
So, \(\frac{m_{p}}{m_{e}}>>1 \Rightarrow \frac{\mu_{e}}{\mu_{p}}>>1\)
\(\Rightarrow\) \(\mu_{e}>>\mu_{p}\)
Thus, as the value of magnetic moment of electron is much more as compared to magnetic moment of proton, so the effect of proton is neglected.






































