Now, suppose that the angle between M and B is \(\theta \) .
Troque on magnetic dipole moment M in magnetic field B,
 \({ \tau }^{ ' }=MBsin\theta \)
Two motions will be identical, if
\(pEsin\theta =MBsin\theta \\ pE=MB\\ E=cB\)
Putting this value in Eq.(i), we get
\(pcB=MB\quad \Rightarrow p=\frac { M }{ c } \) 

As, vertical and horizontal components of magnetic fields are perpendicular to each other. so when their magnitudes are equal, resultant will divide their angle equally.
According to the question,
\(H=\sqrt { 3 } V\)
where, H and V are the horizontal and vertical components of the earth's magnetic field. If angle of dip at that place is , then
\(tan \ \delta =\frac { V }{ H } =\frac { V }{ \sqrt { 3 } V } \ [\therefore \quad H=\sqrt { 3 } V]\)
\(tan\quad \delta =\frac { 1 }{ \sqrt { 3 } } \Rightarrow \quad \delta =\frac { \pi }{ 6 } \)
\(\therefore \) Horizontal component of the earth's magnetic field,
 \(H={ B }_{ e }\quad cos\delta \)
where,  \({ B }_{ e }\)=Earth's magnetic field
\(\frac { H }{ { B }_{ e } } =cos\delta =cos\frac { \pi }{ 6 } =\frac { \sqrt { 3 } }{ 2 }\) 
\(H:{ B }_{ e }=\sqrt { 3 } :2\)

Initially,

Neutral point obtained on equatorial line such that,
    \(\left| { B }_{ H } \right| =\left| { B }_{ e } \right| \)
where, B_H =horizontal component of the earth's magnetic field
B_e = magnetic field due to a bar magnet on its equatorial line
Finally

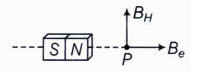
Now, point P comes to an axial line of the magnet and P, net magnetic field is given b
\(B=\sqrt { B_{ a }^{ 2 }+B^{ 2 }_{ H } } =\sqrt { (2B_{ e })^{ 2 }+({ B }_{ H })^{ 2 } } \)
\(=\sqrt { 2{ (B }_{ H })^{ 2 }+B^{ 2 }_{ H } } [\because \quad { B }_{ a }=2{ B }_{ e }]\)
\(=\sqrt { 5 } { B }_{ H }\quad [\because \left| { B }_{ e } \right| =\left| { B }_{ H } \right| ]\)

Susceptibilty of magnetic material \(\chi =\frac { I }{ H } \) where I is the intensity of magnetisation induced in the material and H is the magnetising force.
Diamagnetism is due to orbital motion of electrons in an atom developing magnetic moments opposite to applied field. Thus, the resultant magnetic moment of the diamagnetic material is zero and hence, the susceptibility \(\chi \) of diamagnetic material is not much affected by temperature.
Paramagnetism and ferromagnetism is due to allgnment ot atomic magnetic moments in the direction of the applied field. As temperature is raised, the alignment is disturbed, resulting decrease in susceptibility of both with increase in temperature.

Here, \(\chi _{ m(N_{ 2 }) }=5\times { 10 }^{ -9 }\quad and\quad { \chi }_{ m(Cu) }={ 10 }^{ -5 }\)
\(\frac { \chi _{ m(N_{ 2 }) } }{ { \chi }_{ m(Cu) } } =\frac { 5\times { 10 }^{ -9 } }{ { 10 }^{ -5 } } =5\times { 10 }^{ -4 }\)
As, \({ \chi }_{ m }=\frac { I }{ H } =\frac { M/V }{ H } =\frac { M }{ HV } =\frac { M\rho }{ Hm } \)   
where  M = magnetic moment
V = volume, m = mass and = density
\({ \therefore \ \chi }_{ m }\alpha l\), for given value of \(\frac { M }{ Hm } \)
Thus, \(\frac { \chi _{ m(N_{ 2 }) } }{ { \chi }_{ m(Cu) } } =\frac { { \rho }_{ { N }_{ 2 } } }{ { \rho }_{ { C }u } } =\frac { 28\quad g/22400\quad cc }{ 8\quad g/cc } =1.6\times { 10 }^{ -4 }\)