CBSE 12th Standard Physics Subject Semiconductor Electronics Materials Devices And Simple Circuits 3 Mark Ncert Exemplar Questions 2021
By QB365 on 24 May, 2021
QB365 Provides the updated NCERT Exemplar Questions for Class 12, and also provide the detail solution for each and every case study questions. NCERT Exemplar questions are latest updated question pattern from NCERT, QB365 will helps to get more marks in Exams
QB365 - Question Bank Software
CBSE 12th Standard Physics Subject Semiconductor Electronics Materials Devices And Simple Circuits 3 Mark Ncert Exemplar Questions 2021
12th Standard CBSE
-
Reg.No. :
Physics
-
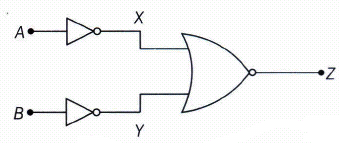
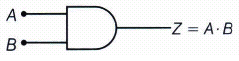
You are given a circuit below. Write its truth table, identify the logic operation carried out by this circuit. Draw the logic symbol of the gate it corresponds.
 (a)
(a) -
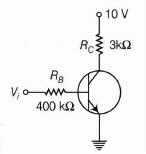
In the circuit shown in figure, when the input voltage of the base resistance is 10 V, VBE is zero and VCE is also zero. Find the values of IB, IC and \(\beta\)
 (a)
(a) -
Predict the effect on the electrical properties of a silicon crystal at room temperature, if every millionth silicon atom temperature, if every millionth silicon atom is replaced by an atom of indium. Given, Concentration of silicon atoms = \(5\times { 10 }^{ 28 }{ m }^{ -3 }\) intrinsic carrier concentration = \(1.5\times { 10 }^{ 16 }{ m }^{ -3 }\) He = 0.135 m3/ V-s and Hh = 0.048 m3 / V-s.
(a) -
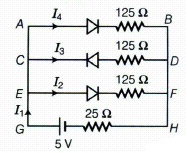
If each diode in figure has a forward bias resistance of \(25\Omega \) and infinite resistance in reverse bias, what will be the values of the currents \(I_{ 1 },I_{ 2 },I_{ 3 } \ and \ I_{ 4 }\) ?
 (a)
(a) -
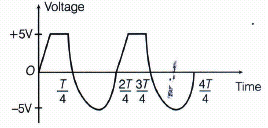
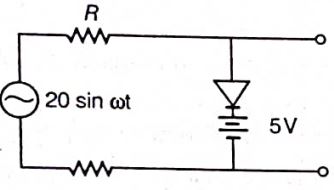
Assuming an ideal diode, draw the output waveform for the circuit given in the figure, explain the waveform.
 (a)
(a)
*****************************************
CBSE 12th Standard Physics Subject Semiconductor Electronics Materials Devices And Simple Circuits 3 Mark Ncert Exemplar Questions 2021 Answer Keys
-
Truth table of given circuit is given below:
A B X=\(\overline { A } \) Y=\(\overline { B } \) \(Z=\overline { \left( X+Y \right) } =\overline { \overline { A } +\overline { B } } \) 0 0 1 1 0 0 1 1 0 0 1 0 0 1 0 1 1 0 0 1 This circuit out the logic operation of AND gate which can be verified also by De-Morgan's theorem
\(Z=\overline { \left( X+Y \right) } =\overline { \overline { A } +\overline { B } } \)
\(Z=\overline { \overline { A } } .\overline { \overline { B } } =A.B\)
This circuit corresponds to AND gate logic symbol is
-
Given voltage across RB = 10 V
\(Resistance,{ R }_{ B }=400\kappa \Omega\)
\( { V }_{ BE }=0,{ V }_{ CE }-0 \ { R }_{ C }=3\kappa \Omega\)
\( { I }_{ B }=\frac { Voltage \ across \ { R }_{ B } }{ { R }_{ B } } =\frac { 10 }{ 400\times { 10 }^{ 3 } } \)
\(25\times { 10 }^{ -6 }A=25\mu A\)
\( Voltage \ across{ R }_{ C }=10 \ V\)
\({ I }_{ C }=\frac { Voltage \ across \ { R }_{ c } }{ { R }_{ C } } =\frac { 10 }{ 3\times { 10 }^{ 3 } }\)
\( \beta =\frac { { I }_{ C } }{ { I }_{ B } } =\frac { 3.33\times { 10 }^{ -3 } }{ 25\times { 10 }^{ -6\\ } }\)
\( \beta =1.33\times { 10 }^{ 2 } \)
\(=133\) -
As, Concentration of Si atom \(=5\times { 10 }^{ 28 }\) /m3
The doping of indium is 1 atom 106 atoms of Si. But indium has three valence electrons and each doped indium atom creates one hole in Si crystal. Hence, it acts as an acceptor atom.
Concentration of acceptor atoms,
\({ n }_{ h }=5\times { 10 }^{ 28 }\times { 10 }^{ -6 }=5\times { 10 }^{ 22 }/{ m }^{ 3 }\)
Intrinsic carrier concentration,
\({ n }_{ i }=1.5\times { 10 }^{ 16 }/{ m }^{ 3 }\)
Hole concentration is increased
\(=\frac { { n }_{ h } }{ { n }_{ i } } =\frac { 5\times { 10 }^{ 22 } }{ 1.5\times { 10 }^{ 16 } } =3.33\times { 10 }^{ 6 }\)
New electron concentration,
\({ n }_{ e }=\frac { { n }_{ i }^{ 2 } }{ { n }_{ b } } =\frac { { \left( 1.5\times { 10 }^{ 16 } \right) }^{ 2 } }{ 5\times { 10 }^{ 22 } } =0.45\times { 10 }^{ 10 }/{ m }^{ 3 }\)
Electron concentration has been reduced
\(=\frac { { n }_{ i } }{ { n }_{ e } } =\frac { 1.5\times { 10 }^{ 16 } }{ 0.45\times { 10 }^{ 10 } } =3.33\times { 10 }^{ 6 }\)/m3
This means that the hole concentration has been increased over its intrinsic concentration by the same amount with which the electron concentration has been decreased.
The conductivity of doped silicon is given by
\(\sigma =e\left( { n }_{ e }H_{ e }+{ n }_{ h }H_{ h } \right) \)
\(\\ =\quad 1.6\times { 10 }^{ -19 }\left( 0.45\times { 10 }^{ 10 }\times 0.135+5\times { 10 }^{ 22 }\times 0.048 \right)\)
= 384 S/m
Resistivity, \(\rho =\frac { 1 }{ \sigma } =\frac { 1 }{ 384 } =0.0026\Omega -m\)
Conductivity of pure Si crystal,
\(\sigma ={ en }_{ i }\left( { H }_{ e }+{ H }_{ h } \right) \)
\(\\ =1.6\times { 10 }^{ -19 }\times 1.5\times { 10 }^{ 16 }\left( 0.135+0.048 \right) \)
\(\\ =0.4392\times { 10 }^{ -3 }S/m\)
Resistivity, \(\rho =\frac { 1 }{ \sigma } =\frac { 1 }{ 0.4392\times { 10 }^{ -3 } } =2276.\Omega -m\)
Thus, we see that the conductivity of doped Si becomes much greater than its intrinsic conductivity and the resistivity has become much smaller than the intrinsic resistivity. -
Given, forward biased resistance = \(25\Omega \)
Reverse biased resistance = \(\infty \)
As the diode in branch CD is in reverse biased which having resistance infinite.
so \(I_{ 3 }\)= 0
Resistance in branch AB = 25 + 125 = 150\(\Omega \)(say R1)
Resistance in branch EF = 25 + 125 = 150\(\Omega \)(say R2)
AB is parallel to EF.
so, resultant resistance, \(\frac { 1 }{ { R }^{ \prime } } =\frac { 1 }{ { R }_{ 1 } } +\frac { 1 }{ { R }_{ 2 } } =\frac { 1 }{ 150 } +\frac { 1 }{ 150 } =\frac { 2 }{ 150 } \)
\(\Rightarrow { R }^{ \prime }=75\Omega \)
Total resistance, \(R={ R }^{ \prime }+25=75+25=100\Omega \)
Current, \({ I }_{ 1 }=\frac { V }{ R } =\frac { 5 }{ 100 } =0.05A\)
\({ I }_{ 1 }={ I }_{ 4 }+{ I }_{ 2 }+{ I }_{ 3 }\quad [Here,\quad { I }_{ 3 }=0]\)
\(\\ { I }_{ 1 }={ I }_{ 4 }+{ I }_{ 2 }\)
Here, the resistances R1 and R2 are same
\({ I }_{ 4 }={ I }_{ 2 }\)
\(\\ { I }_{ 1 }=2{ I }_{ 2 }\)
\(\\ \Rightarrow { I }_{ 2 }=\frac { { I }_{ 1 } }{ 2 } =\frac { 0.05 }{ 2 } =0.025A\)
\(\\ { I }_{ 4 }=0.025A\)
\(\\ { I }_{ 1 }=0.05A\)
\(\\ { I }_{ 2 }=0.025A\)
\(\\ { I }_{ 3 }=0\)
\(\\ { I }_{ 4 }=0.025A\) -
When the input voltage is equal to or less than 5 V, diode will be reverse biased. It will offer high resistance in comparison to resistance (R) in series. now, diode appears in open circuit. The input waveform is then passed to the output terminals. The result with sine wave input is to dip off all positive going portion above 5 V.
If the input voltage is more than +5V, the diode will be conducting as forward biased offering low resistance in comparison to R. But there will be no voltage in output beyond 5 V as the voltage beyond +5V will appear across R.
When input voltage is negative, input voltage becomes more than -5 V (due to 5V battery in reverse bias position), the diode will be reverse biased. It will offer high resistance in comparison to resistance R in series. Now, junction diode appears in open circuit. The input waveform is then passed on to the output terminals. The output waveform is shown here in the figure