CBSE 12th Standard Physics Subject Wave Optics HOT Questions 3 Mark Questions 2021
By QB365 on 27 May, 2021
QB365 Provides the HOT Question Papers for Class 12 Physics, and also provide the detail solution for each and every HOT Questions. HOT Questions will help to get more idea about question pattern in every exams and also will help to get more marks in Exams
QB365 - Question Bank Software
CBSE 12th Standard Physics Subject Wave Optics HOT Questions 3 Mark Questions 2021
12th Standard CBSE
-
Reg.No. :
Physics
-
A convex lens of focal length 30 cm is placed coaxially with a convex mirror of radius of curvature 20 cm. The two are kept at 15 cm from each other. A point object lies 60 cm in front of the convex lens. Draw a ray diagram to show the formulation of the image by the combination. Determine the nature and position of the image formed.
(a) -
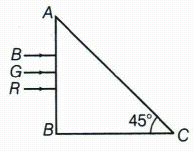
Three light rays, red(R), green(G) and blue (B) are incident on a right angled prism ABC at face AB. The refractive indices of the material of the priam for red, green and blue wavelengths are 1.39, 1.44 and 1.47, respectively.Out of the three, which colour of ray will emerge out of face AC? Justify your answer.Trace the path of these rays after passing through face AB.
 (a)
(a) -
A jar of height is filled with a transparent liquid of refractive index \(\mu \)(figure). At the centre of the jar on the bottom surface is a dot. Find the minimum diameter of a disc, such that when placed on the top surface symmetrically about the centre, the dot is invisible.
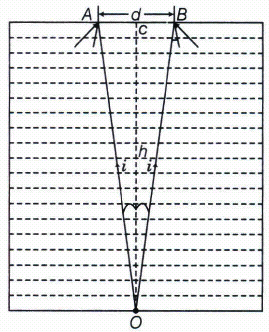
The problem is based on the principle of total inter reflection and area of visibility.(a) -
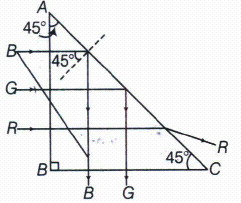
Show that for a material with refractive index \(\mu \ge \sqrt { 2 } \), light incident at any angle shall be guided along a length perpendicular to the incident face.
(a) -
(i) Light passes through two polaroids \({ P }_{ 1 }and{ P }_{ 2 }\) with pass axis of \({ P }_{ 2 }\) with pass axis of \({ P }_{ 2 }\) making in angle \(\theta \) with the pass axis of \({ P }_{ 1 }\) . For what value of \(\theta \) is the intensity of emergent light zero?
(ii) A third polaroid is placed between \({ P }_{ 1 }and{ P }_{ 2 }\) with its pass axis making an angle \(\beta \) with the pass axis is \({ P }_{ 1 }\) . Find the value of \(\beta \) for which the intensity of light from \({ P }_{ 2 }\) is \(\frac { { I }_{ 0 } }{ 8 } \) , where \({ I }_{ 0 }\) is the intensity of light on the polaroid \({ P }_{ 1 }\) .(a)
*****************************************
CBSE 12th Standard Physics Subject Wave Optics HOT Questions 3 Mark Questions 2021 Answer Keys
-
The ray diagram showing the image formation is given below:
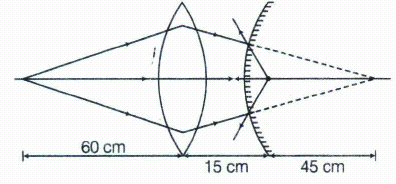
O is at 2f of lens, so it will form image at 2f on other side, i.e. 60 cm from lens. Hence, position of object from mirror is at (60 - 15) cm = 45 cm behind the mirror.
For mirror,
\(f=+10cm,\)
\( u=+45cm,\ v=?\)
As, \(\frac { 1 }{ v } +\frac { 1 }{ u } =\frac { 1 }{ f } \)
\(\Rightarrow \ \frac { 1 }{ v } +\frac { 1 }{ 45 } =\frac { 1 }{ 10 } \)
\( \therefore \ v=+\frac { 90 }{ 7 } cm\) (behind be mirror) -
By geometry, angle of incidence (i) at face AC for all three rays is 45\(^{0}\). Light suffers total internal reflection for which this angle of incidence is greater than critical angle.
i>ic, \(\Rightarrow\)sin i > sin ic
or sin 45\(^{0}\) > sin ic \(\Rightarrow\) \(\frac { 1 }{ sin{ 45 }^{ 0 } } <\frac { 1 }{ sin{ i }_{ c } } \Longrightarrow \sqrt { 2 } <\mu \)
Total internal reflection takes place on AC for rays with \(\mu >\sqrt { 2 } =1.414,\) i.e., green and blue colour sukker. Total internal reflection whereas red undergoes refraction.
-
Let d be the diameter of the disc. The sopt shall be invisible, if the incident rays OA and OB suffer total internal reflection.
Let i be the angle of incidence
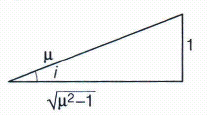
Using relationship between refractive index and critical angle, then
\(\sin { i=\frac { 1 }{ \mu } }\)
Using geometry and trigonometry,
Now,
\(\frac { d/2 }{ h } =\tan { i } \Rightarrow \frac { d }{ 2 } =h\tan { i } =h[\sqrt { { \mu }^{ 2 }-1{ ] }^{ -1 } }\)
\( [\because \ From \ the \ figure,\ tani=\frac { 1 }{ \sqrt { { \mu }^{ 2 } } -1 } ]\)
\( d=\frac { 2h }{ \sqrt { { \mu }^{ 2 } } -1 } \)
This is required expression of d. -
Any ray entering at an angle i shall be guided along AC, if the ray makes an angle \(\phi \) with the face AC greater than the critical angle as the principle of total internal reflection,\(\phi \)+r = 90o, therefore, sin \(\phi \) = cos r.
\(\Rightarrow \ sin\phi \ge \frac { 1 }{ \mu } \ \Rightarrow \ cos\ r\ge \frac { 1 }{ \mu } \)
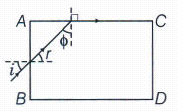
or \(1-{ cos }^{ 2 }r\le 1-\frac { 1 }{ { \mu }^{ 2 } } \Rightarrow { sin }^{ 2 }r\le 1-\frac { 1 }{ { \mu }^{ 2 } } \left[ \therefore 1-{ cos }^{ 2 }r={ sin }^{ 2 }r \right] \) -
(i) By Malus law, intensity of emergent light from \({ P }_{ 2 }\) is \(I={ I }_{ \circ }cos^{ 2 }\theta \) , where \(\theta \) is the angle between \({ P }_{ 1 }and{ P }_{ 2 }\)|
When \(\theta ={ 90 }^{ \circ }\)
\(\\ I={ I }_{ \circ }\times 0\)
Intensity of emergent light, I = 0
(ii) Intensity of light from \({ P }_{ 3 }\)
\(=\left( \frac { { I }_{ \circ } }{ 2 } cos^{ 2 }\beta \right) \left[ cos^{ 2 }\left( { 90 }^{ \circ }-\beta \right) \right] \)
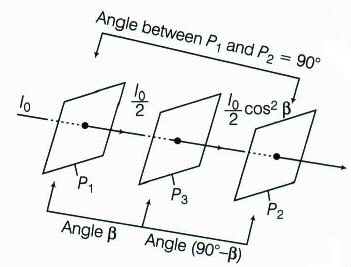
\(=\frac { { I }_{ \circ } }{ 2 } cos^{ 2 }\beta sin^{ 2 }\beta =\frac { { I }_{ \circ } }{ 8 } sin^{ 2 }2\beta \)
\(As,\ \frac { { I }_{ \circ } }{ 8 } sin^{ 2 }2\beta =\frac { { I }_{ \circ } }{ 8 } (given)\)
\(so, \ \left( sin2\beta \right) ^{ 2 }=1 \ \Rightarrow 2\beta ={ 90 }^{ \circ } \ \Rightarrow \beta ={ 45 }^{ \circ }\)






































