Given, object distance,u = -3cm
Radius of curvature, R = -24cm
\(f=\frac { R }{ 2 } =-\frac { -24 }{ 2 } =-12cm\)
According to mirror formula,
\(\frac { 1 }{ f } =\frac { 1 }{ v } +\frac { 1 }{ u } \)
\(\Rightarrow \ \frac { 1 }{ v } =\frac { 1 }{ f } -\frac { 1 }{ u } =\frac { 1 }{ -12 } -\frac { 1 }{ -3 } \)         
\(\Rightarrow \frac { 1 }{ v } =\frac { 1 }{ -12 } +\frac { 1 }{ 3 } \)
\( \Rightarrow \ \frac { 1 }{ v } =\frac { -1+4 }{ 12 }\)
\( \Rightarrow \ v=4cm\)            ​​​
Magnification, \(m=-\frac { v }{ u } =\frac { -4 }{ -3 } =+1.33\)
i.e. the image formed is virtual, erect and magnified.

Given, focal length, f =  +30cm
Magnification, m \(=\frac { 1 }{ 4 } ,v=?\)
We know that,
\(m=\frac { f-v }{ f } \) 
\(\Rightarrow \ \frac { 1 }{ 4 } =\frac { 30-v }{ 30 } \)
\( \Rightarrow 30=120-4v\)
\( \Rightarrow \ v=\frac { 90 }{ 4 } =+22.5cm\)
As, v is positive, therefore a virtual and erect image will be formed on other side of the object.

R₁ = 20 cm
R₂ = -40 cm
f = 20 cm, n = ?
\(\frac { 1 }{ f } =(n-1)\frac { 1 }{ R_{ 1 } } -\frac { 1 }{ R_{ 2 } }\)
\(\frac { 1 }{ 20 } =(n-1)\frac { 1 }{ 20 } +\frac { 1 }{ 40 } \Rightarrow \frac { 1 }{ n-1 } =20(\frac { 2+1 }{ 40 } )=\frac { 3 }{ 2 }\)
\( n-1=\frac { 2 }{ 3 } \Rightarrow 3n=5\Rightarrow n=\frac { 5 }{ 3 } \)

(i) The ray diagram for the formation of the image of the mobile phone is shown below. The image of the part which is on the plane perpendicular to principal axis will be on the same plane. It will be of the same size, i.e. \({ B }^{ \prime }C=BC\)

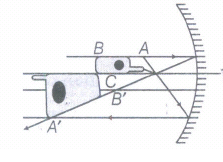
(ii) We may think that the image will now show only half of the object, but considering the laws of reflection to be true for all points of the remaining part of the mirror, the image will be that of the whole object.

However, as the area of the reflecting surface has been reduced, the intensity of the image will be low, i.e. half.

For convex mirror, f >
Also, u < 0
but from mirror equation,
\(\frac { 1 }{ f } =\frac { 1 }{ v } +\frac { 1 }{ u } =\frac { 1 }{ v } +\frac { 1 }{ \left| -u \right| } \ \left[ taking \ u \ with \ sign \right]\)
\( \frac { 1 }{ v } =\frac { 1 }{ f } +\frac { 1 }{ u } \)
\( \Rightarrow f \ and \ u \ to \ be \ positive, \ then\)
\(\frac { 1 }{ v } >0\Rightarrow \ v>0\)
Hence, virtual image is formed.
(iii) For concave mirror,
f < 0, u < 0, \(\left| f \right| >\left| u \right| >0\)
But from mirror equation,
\(\frac { 1 }{ f } =\frac { 1 }{ v } +\frac { 1 }{ u }\)
\( \Rightarrow \frac { -1 }{ \left| f \right| } =\frac { 1 }{ v } -\frac { 1 }{ \left| u \right| }\)
\( \frac { 1 }{ v } =\frac { 1 }{ \left| u \right| } -\frac { 1 }{ \left| f \right| }\)
\(\because \ \left| v \right| <\left| f \right|\)
\(\Rightarrow \frac { 1 }{ \left| u \right| } >\frac { 1 }{ \left| f \right| }\)
\(\Rightarrow \ \frac { 1 }{ v } >0 \ \Rightarrow \ v>0\)
Image is formed on RHS of mirror, i.e. virtual image.
Also, \(\frac { 1 }{ \left| f \right| } =\frac { 1 }{ v } -\frac { 1 }{ \left| u \right| } \)
For concave mirror, f is negative.
\(\Rightarrow \frac { 1 }{ \left| v \right| } <\frac { 1 }{ \left| u \right| } \Rightarrow \frac { \left| v \right| }{ \left| u \right| } >1\Rightarrow m>1\)
Enlarged virtual image formed on the other side of mirror.