CBSE 12th Standard Physics Subject Wave Optics Ncert Exemplar 3 Mark Questions With Solution 2021
By QB365 on 24 May, 2021
QB365 Provides the updated NCERT Exemplar Questions for Class 12, and also provide the detail solution for each and every case study questions. NCERT Exemplar questions are latest updated question pattern from NCERT, QB365 will helps to get more marks in Exams
QB365 - Question Bank Software
CBSE 12th Standard Physics Subject Wave Optics Ncert Exemplar 3 Mark Questions With Solution 2021
12th Standard CBSE
-
Reg.No. :
Physics
-
A person with a normal near point (25 cm) using a compound microscope with objective of focal length 8.0 mm and an eyepiece of focal length 2.5 cm can bring an object placed at 9.0 mm from the objective in sharp focus.What is the separation between the two lenses?Calculate the magnifying power of the microscope.
(a) -
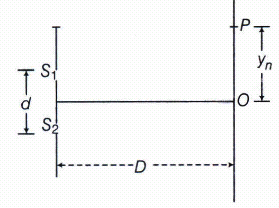
The intensity at the central maxima (O) in a Young's double experiment is \(I^o\). If the distance OP equals one-third of fringe width of the pattern, show that the intensity at point P would be I0 / 4
 (a)
(a) -
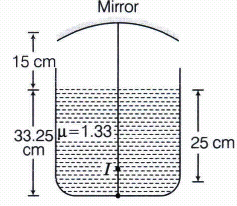
A container is filled with water (\(\mu \) = 1.33) upto a height of 33.25 cm. A concave mirror is placed 15 cm above the water level and the image of an object placed at the bottom is formed 25 cm below the water level. What will be the focal length?
 (a)
(a) -
Can reflection result in a plane polarised light, if the light is incident on the interface from the side with higher refractive index?
(a) -
In an experiment with two coherent sources, the amplitude of the intensity variation is found to be 5% of the average intensity. What will be the relative intensities of the light waves of interfering source.
(a)
*****************************************
CBSE 12th Standard Physics Subject Wave Optics Ncert Exemplar 3 Mark Questions With Solution 2021 Answer Keys
-
Given, focal length of objective, f0 = 8mm = 0.8 cm
Focal length of eyepiece, fe = 2.5 cm
Distance of object from objective, u0 = - 9 mm = - 0.9 cm
Distance of image from eyepiece, ve = - D = - 25 cm
Using lens formula for eyepiece, \(\frac { 1 }{ { v }_{ e } } -\frac { 1 }{ { u }_{ e } } =\frac { 1 }{ { f }_{ e } } \\ \)
or \(\frac { 1 }{ { u }_{ e } } =\frac { 1 }{ { v }_{ e } } -\frac { 1 }{ { f }_{ e } } =-\frac { 1 }{ 25 } -\frac { 1 }{ 2.5 } =\frac { -1-10 }{ 25 } =-\frac { 11 }{ 25 } \\ \)
ue = - 2.27 cm
Using lens formula for objective, \(\frac { 1 }{ { v }_{ e } } -\frac { 1 }{ { u }_{ 0 } } =\frac { 1 }{ { f }_{ 0 } } \)
or \(\frac { 1 }{ { v }_{ 0 } } =\frac { 1 }{ { f }_{ 0 } } +\frac { 1 }{ { u }_{ 0 } } =-\frac { 1 }{ 0.8 } -\frac { 1 }{ 0.9 } =-\frac { 0.9-0.8 }{ 0.72 } =\frac { 0.1 }{ 0.72 } \\ \)
Distance of image for objective lens, v0 = 7.2 cm
Separation between two lenses,
\(L=|{ u }_{ e }|+|{ v }_{ 0 }|=2.27+7.2=9.47 \ cm\)
Magnifying power of co,pound microscope,
\(m=\frac { { v }_{ o } }{ { u }_{ 0 } } (1+\frac { D }{ { f }_{ e } } )=\frac { 7.2 }{ 0.9 } (1+\frac { 25 }{ 2.5 } )=88\) -
Intensity can be found out, if we know the phase difference. Phase difference can be calculated with the help of path difference. So first of all, path difference will be calculated.
Given, \(OP={ y }_{ n }\)
The distance OP equals one-third of frings width of the pattern.
i.e \({ y }_{ n }=\frac { \beta }{ 3 } =\frac { 1 }{ 3 } \left( \frac { D\lambda }{ d } \right) =\frac { D\lambda }{ 3d } \)
\(\Rightarrow \ \frac { { dy }_{ n } }{ D } =\frac { \lambda }{ 3 } \)
Path difference=\({ S }_{ 2 }P-{ S }_{ 1 }P=\frac { { dy }_{ n } }{ D } =\frac { \lambda }{ 3 } \)
\(\therefore \) Phase difference, \(\phi =\frac { 2\pi }{ \lambda } \times \)path difference
\(\frac { 2\pi }{ \lambda } \times \frac { \lambda }{ 3 } =\frac { 2\pi }{ 3 } \)
If intensuty at central frings is \(I^o\), then intensity at a point P, where phase difference \(\phi \) is given by
\(I=I^o\)\({ cos }^{ 2 }\phi \)
\(I=I^o\)\({ \left( cos\frac { 2\pi }{ 3 } \right) }^{ 2 }\)
= \(I^o\)\({ \left( -cos\frac { \pi }{ 3 } \right) }^{ 2 }\)=\(I^o\)\({ \left( -\frac { 1 }{ 2 } \right) }^{ 2 }\)=\(\quad \frac { { I }_{ \circ } }{ 4 } \)
Hence, the intensity at point p would be \( \frac { { I }_{ \circ } }{ 4 } \). -
-18.3 cm
-
When angle of incidence is equal to Brewster's angle, the transmitted light is unpolarised and reflected light is plane polarised. Consider the diagram in which unpolarised light is represented by dot and plane polarised light is represented by arrows.
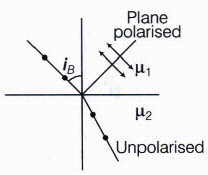
Polarised by reflection occurs, when the angle of incidence is equal to the Brewster's angle. i.e. \(tani_{ B }=^{ 1 }{ \mu }_{ 2 }=\frac { { \mu }_{ 2 } }{ { \mu }_{ 1 } } ,\ where{ \ \mu }_{ 2 }<{ \mu }_{ 1 }\)
When the light rays travel in such a medium, the critical angle is expressed as \(sini_{ c }=\frac { { \mu }_{ 2 } }{ { \mu }_{ 1 } } \ where,{ \ \mu }_{ 2 }<{ \mu }_{ 1 }\)
As, \(|tani_{ B }|>|sini_{ c }|\) for large angles
Thus, definitely polarisation by reflection will occur. -
As we know that, \(I={ I }_{ av }\pm 0.05{ I }_{ av }\)
\(\Rightarrow \) \({ I }_{ max }={ I }_{ av }\left( 1+0.05 \right) =1.05{ I }_{ av }\)
\({ I }_{ min }={ I }_{ av }\left( 1-0.05 \right) =0.95{ I }_{ av }\)
Dividing Eqs. (i) and (ii), we get
\(\Rightarrow \) \(\frac { { I }_{ max } }{ { I }_{ min } } =\frac { 1.05 }{ 0.95 } \)
\(\Rightarrow \) \(\left( \frac { r+1 }{ r-1 } \right) ^{ 2 }=\frac { 105 }{ 95 } \)
\(\Rightarrow \) \({ r }^{ 2 }+1+2r)95=105({ r }^{ 2 }+1-2r)\)
\(\Rightarrow \) \({ 10r }^{ 2 }-400r+10=0\Rightarrow r=40\)
\(\frac { { I }_{ 1 } }{ { I }_{ 2 } } ={ r }^{ 2 }=({ 40) }^{ 2 }=1600:1\)






































