Class 10th Maths - Coordinate Geometry Case Study Questions and Answers 2022 - 2023
By QB365 on 09 Sep, 2022
QB365 provides a detailed and simple solution for every Possible Case Study Questions in Class 10th Maths Subject - Coordinate Geometry, CBSE. It will help Students to get more practice questions, Students can Practice these question papers in addition to score best marks.
QB365 - Question Bank Software
Coordinate Geometry Case Study Questions With Answer Key
10th Standard CBSE
-
Reg.No. :
Maths
-
The Chief Minister of Delhi launched the, 'Switch Delhi: an electric vehicle mass awareness campaign in the National Capital. The government has also issued tenders for setting up 100 charging stations across the city. Each station will have five charging points. For demo charging station is set up along a straight line and has charging points at \(A\left(\frac{-7}{3}, 0\right), B\left(0, \frac{7}{4}\right)\), C(3, 4), D(7, 7) and E(x, y). Also, the distance between C and E is 10 units.

Based on the above information, answer the following questions.
(i) The distance DE is(a) 5 units (b) 10 units (c) 4 units (d) 6units (ii) The value of x + y is
(a) 20 (b) 21 (c) 22 (d) 23 (iii) Which of the following is true?
(a) The points C, D and E are vertices of a triangle (b) The points C, D and E are collinear (c) The points C, D and E lie on a circle (d) None of these (iv) The ratio in which B divides AC is
(a) 9:7 (b) 4:7 (c) 7:4 (d) 7:9 (v) Which of the following equations is satisfied by the given points?
(a) x + y = 0 (b) x - y = 0 (c) 3x - 4y + 7 = 0 (d) 3x+4y+7=0 (a) -
Alia and Shagun are friends living on the same street in Patel Nagar. Shaguns house is at the intersection of one street with another street on which there is a library. They both study in the same school and that is not far from Shagun's house. Suppose the school is situated at the point 0, i.e., the origin, Alia's house is at A. Shaguns house is at B and library is at C. Based on the above information, answer the following questions.
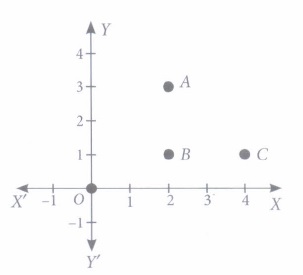
(i) How far is Alia's house from Shaguns house?(a) 3 units (b) 4 units (c) 5 units (d) 2 units (ii) How far is the library from Shaguns house?
(a) 3 units (b) 2 units (c) 5 units (d) 4 units (iii) How far is the library from Alia's house?
(a) 2 units (b) 3 units (c) 4 units (d) (d) None of these (iv) Which of the following is true?
(a) ABC forms a scalene triangle (b) ABC forms an isosceles triangle (c) ABC forms an equilateral triangle (d) None of these (v) How far is the school from Alia's house than Shaguns house?
(a) \(\sqrt(13)\) units (b) \(\sqrt(5)\) units (c) (\(\sqrt(13)\) + \(\sqrt(5)\) )units (d) (\(\sqrt(13)\) - \(\sqrt(5)\) ) units (a) -
A person is riding his bike on a straight road towards East from his college to city A and then to city B. At some point in between city A and city B, he suddenly realises that there is not enough petrol for the journey. Also, there is no petrol pump on the road between these two cities.
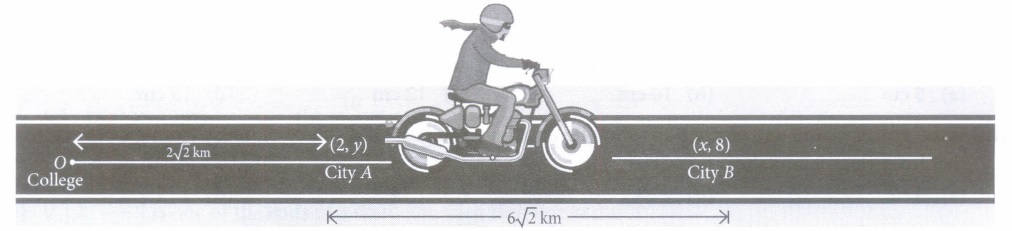
Based on the above information, answer the following questions.
(i) The value of y is equal to(a) 2 (b) 3 (c) 4 (d) 5 (ii) The value of x is equal to
(a) 4 (b) 5 (c) 8 (d) 7 (iii) If M is any point exactly in between city A and city B, then coordinates of M are
(a) 3,3 (b) 4,4 (c) 5,5 (d) 6,6 (iv) The ratio in which A divides the line segment joining the points O and M is
(a) 1:2 (b) 2.1 (c) 3.2 (d) 2.3 (v) If the person analyse the petrol at the point M(the mid point of AB), then what should be his decision?
(a) Should he travel back to college (b) Should try his luck to move towards city B (c) Should be travel back to city A (d) None of these (a) -
Satellite image of a colony is shown below. In this view, a particular house is pointed out by a flag, which is situated at the point of intersection of x and y-axes. If we go 2 em east and 3 em north from the house, then we reach to a Grocery store. If we go 4 em west and 6 em south from the house, then we reach to a Electrician's shop. If we go 6 em east and 8 em south from the house, then we reach to a food cart. If we go 6 em west and 8 em north from the house, then we reach to a bus stand.
Based on the above information, answer the following questions.
(i) The distance between grocery store and food cart is(a) 12 cm (b) 15 cm (c) 18 cm (d) none of these (ii) The distance of the bus stand from the house is
(a) 5 cm (b) 10 cm (c) 12 cm (d) 15 cm (iii) If the grocery store and electrician's shop lie on a line, the ratio of distance of house from grocery store to that from electrician's shop, is
(a) 3.2 (b) 2.3 (c) 1.2 (d) 2.1 (iv) The ratio of distances of house from bus stand to food cart is
(a) 1.2 (b) 2.1 (c) 1.1 (d) none of these (v) The coordinates of positions of bus stand, grocery store, food cart and electrician's shop form a
(a) rectangle (b) parallelogram (c) square (d) none of these (a) -
A round clock is traced on a graph paper as shown below. The boundary intersect the coordinate axis at a distance of 4/3 units from origin.
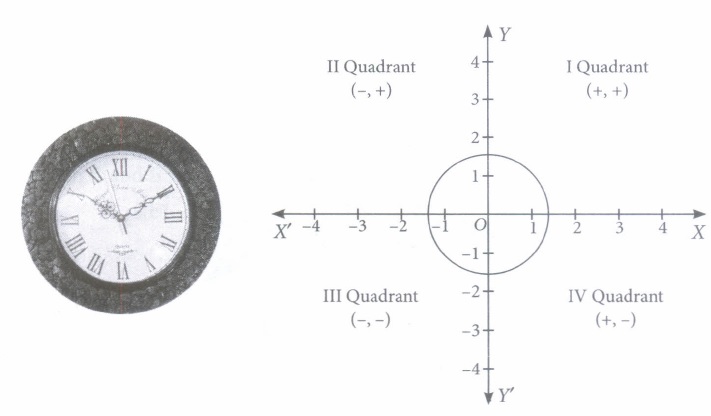
Based on the above information, answer the following questions .
(i) Circle intersect the positive y-axis at\(A\left(\frac{2}{3}, 0\right),\) \((b) \left(0, \frac{2}{3}\right)\) \((c) \left(0, \frac{4}{3}\right)\) \((d) \left(\frac{4}{3}, 0\right)\) (ii) The centre of circle is the
(a) mid-point of points of intersection with x-axis (b) mid-point of points of intersection with y-axis (c) both (a) and (b) (d) none of these (iii) The radius of the circle is
\((a) \frac{4}{3} units\) \((b) \frac{3}{2} units\) \((c) \frac{2}{3} units\) \((d) \frac{3}{4} units\) (iv) The area of the circle is
\((a) 16 \pi^{2} sq. units\) \((b) \frac{16}{9} \pi sq. units\) \((c) \frac{4}{9} \pi^{2} sq. units\) \((d) 4 \pi sq. units\) (v) If \(\left(1, \frac{\sqrt{7}}{3}\right)\) is one of the ends of a diameter, then its other end is
\((a) \left(-1, \frac{\sqrt{7}}{3}\right)\) \((b) \left(1,-\frac{\sqrt{7}}{3}\right)\) \((c) \left(1, \frac{\sqrt{7}}{3}\right)\) \((d) \left(-1,-\frac{\sqrt{7}}{3}\right)\) (a) -
To raise social awareness about hazards of smoking, a school decided to start 'No smoking' campaign. 10 students are asked to prepare campaign banners in the shape of a triangle. The vertices of one of the triangle are P( -3,4), Q(3, 4) and R(-2, -1).

Based on the above information, answer the following questions.
(i) The coordinates of centroid of \(\Delta\)PQR are\((a) \left(\frac{2}{3}, \frac{7}{3}\right)^{n}\) \((b) \left(\frac{1}{3}, \frac{1}{3}\right)\) \((c) \left(\frac{-2}{3}, \frac{7}{3}\right)\) \((d) \left(\frac{7}{3}, \frac{2}{3}\right)\) (ii) If S be the mid-point of line joining P and Q, then coordinates of S are
(a) (4,0) (b) (2,0) (c) (0,2) (d) (0,4) (iii) If T be the mid-point of line joining Rand Q, then coordinates of T are
\((a) \left(\frac{1}{2}, \frac{1}{2}\right)\) \((b) \left(\frac{3}{2}, \frac{1}{2}\right)\) \((c) \left(\frac{1}{2}, \frac{3}{2}\right)\) (d) none of these (iv) If Ube the mid-point of line joining Rand P, then coordinates of U are
\((a) \left(-\frac{5}{2}, \frac{3}{2}\right)\) \((b) \left(\frac{3}{2},-\frac{5}{2}\right)\) \((c) \left(\frac{3}{2}, \frac{5}{2}\right)\) \((d) \left(\frac{5}{2}, \frac{3}{2}\right)\) (v) The coordinates of centroid of \(\Delta\)STU are
\((a) \left(\frac{2}{3}, \frac{7}{3}\right)\) \((b) \left(\frac{1}{3}, \frac{1}{3}\right)\) \((c) \left(-\frac{2}{3}, \frac{7}{3}\right)\) \((d) \left(\frac{7}{3}, \frac{2}{3}\right)\) (a) -
There are two routes to travel from source A to destination B by bus. First bus reaches at B via point C and second bus reaches from A to B directly. The position of A, Band C are represented in the following graph:
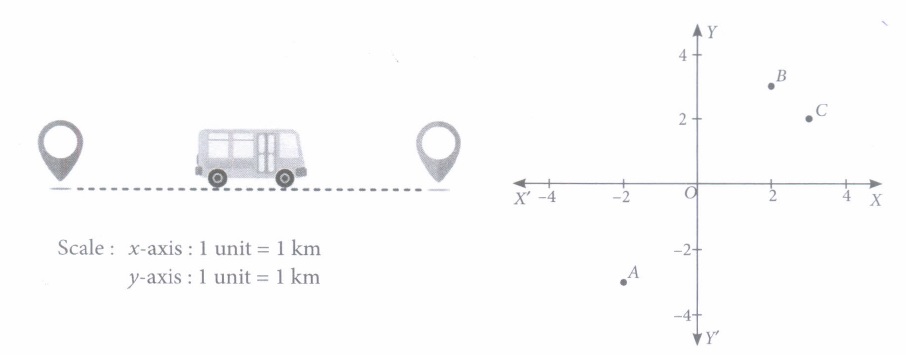
Based on the above information, answer the following questions.
(i) The distance between A and B is(a) 13 km (b) 26 km (c) \(\sqrt{13}\)km (d) none of these (ii) The distance between A and Cis
(a) 5 km (b) 2 km (c) \(\sqrt{5}\)km (d) \(5\sqrt{2}\) km (iii) If it is assumed that both buses have same speed, then by which bus do you want to travel from A to B?
(a) Firstbus (b) Secondbus (c) Any of them (d) None of these (iv) If the fare for first bus is Rs10/km, then what will be the fare for total journey by that bus?
(a) Rs 83 (b) Rs 38 (c) Rs 45 (d) none of these (v) If the fare for second bus is Rs 15/km, then what will be the fare to reach to the destination by this bus?
(a) Rs 105 (b) Rs 108 (c) Rs 110 (d) Rs 115 (a) -
Students of residential society undertake to work for the campaign "Say no to Plastics': Group A took the region under the coordinates (3, 3), (6, y), (x, 7) and (5, 6) and group B took the region under the coordinates (1, 3), (2,6), (5,7) and (4, 4).

Based on the above information, answer the following questions.
(i) If region covered by group A forms a parallelogram, where the coordinates are taken in the given order, then(a) x=8,y=4 (b) x=4,y=8 (c) x=2,y=4 (d) x=4,y=2 (ii) Perimeter of the region covered by group A is
(a) \(\sqrt{10}\) units (b) \(\sqrt{13}\)units (c) \(\sqrt{10}\) + \(\sqrt{13}\)units (d) none of these (iii) If the coordinates of region covered by group B, taken in the same order forms a quadrilateral, then the length of each of its diagonals is
(a) \(4\sqrt{2}\) units, \(2\sqrt{2}\) units (b) \(6\sqrt{2}\) units, \(\sqrt{2}\) units (c) \(3\sqrt{2}\) units, \(2\sqrt{2}\) units (d) none of these (iv) If region covered by group B forms a rhombus, where the coordinates are taken in given order, then the perimeter of this region is
(a) \(\sqrt{10}\) units (b) \(2\sqrt{10}\)units (c) \(3\sqrt{10}\) units (d) \(4\sqrt{10}\) units (v) The coordinates of the point which divides the join of points P(x1, y1) and Q(x2, y2) internally in the ratio m: n is
\(\text { (a) }\left(\frac{m x_{2}+n y_{2}}{m+n}, \frac{m x_{1}+n y_{1}}{m+n}\right)\) \(\text { (b) }\left(\frac{m x_{1}+n y_{1}}{m+n}, \frac{m x_{2}+n y_{2}}{m+n}\right)\) \(\text { (c) }\left(\frac{m x_{2}+n x_{1}}{m+n}, \frac{m y_{2}+n y_{1}}{m+n}\right)\) (d) none of these (a) -
In an examination hall, students are seated at a distance of 2 m from each other, to maintain the social distance due to CORONA virus pandemic. Let three students sit at points A, Band C whose coordinates are (4, -3), (7,3) and (8, 5) respectively.

Based on the above information, answer the following questions.
(i) The distance between A and C is(a) \(\sqrt{5}\) units (b) \(4\sqrt{5}\) units (c) \(3\sqrt{5}\) units (d) none of these (ii) If an invigilator at the point I, lying on the straight line joining Band C such that it divides the distance between them in the ratio of 1 : 2. Then coordinates of I are
\((a) \left(\frac{22}{3}, \frac{11}{3}\right)\) \((b) \left(\frac{23}{3}, \frac{13}{3}\right)\) (c) (6,1) (d) (9,1) (iii) The mid-point of the line segment joining A and C is
(a) (1.6) (b) (6.1) \(\text { (c) }\left(\frac{11}{2}, 0\right)\) (d) none of these (iv) The ratio in which B divides the line segment joining A and C is
(a) 2:1 (b) 3:1 (c) 1:2 (d) none of these (v) The points A, Band C lie on
(a) a straight line (b) an equilateral triangle (c) a scalene triangle (d) an isosceles triangle (a) -
A design of Christmas tree is shown in the following graph:
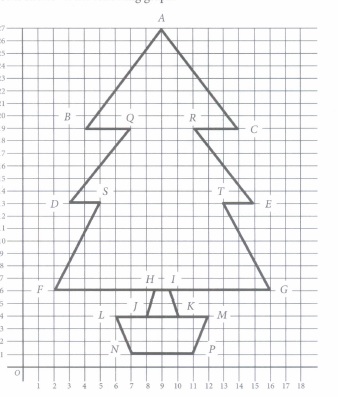
Now answer the following questions.
(i) The distance of point A from x-axis is(a) 9 units (b) 26 units (c) 27 units (d) 10 units (ii) Length of BC is
(a) 12 units (b) 10 units (c) 8 units (d) 6 units (iii) Length of FG is
(a) 10 units (b) 12 units (c) 14 units (d) 16 units (iv) The mid-point of FG lies on line represented by
(a) x = 9 (b) x = 10 (c) x = 8 (d) none of these (v) The perimeter of its trunk LMPN is
(a) \(\sqrt{10}\) units (b) \(2\sqrt{10}\) units (c) 10 units (d) none of these (a) -
The camping alpine tent is usually made using high quality canvas and it is water proof. These alpine tents are mostly used in hilly areas, as the snow will not settle on the tent and make it damp. It is easy to layout and one need not use a manual to set it up. One alpine tent is shown in the figure given below, which has two triangular faces and three rectangular faces. Also, the image of canvas on graph paper is shown in the adjacent figure.
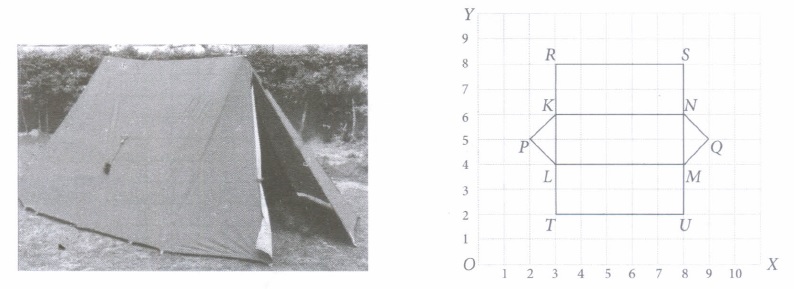
Based on the above information, answer the following questions.
(i) Distance of point Q from y-axis is(a) 9 units (b) 8 units (c) 4 units (d) 5 units (ii) What are the coordinates of U?
(a) (2,8) (b) (8,2) (c) (6,9) (d) (9,6) (iii) The distance between the points P and Q is
(a) 4 units (b) 5 units (c) 6 units (d) 7 units (iv) If a point A(x, y) is equidistant from Rand T, then
(a) y - 2 = 0 (b) y - 3 = 0 (c) y-5=0 (d) y - 6 = 0 (v) Perimeter of image of a rectangular face is
(a) 5 units (b) 8 units (c) 10 units (d) 14 units (a) -
An award function of a Multi National Company (MNC) is arranged in a rectangular shaped meeting room PQRS. 200 flower vases placed along two sides of a room, at a distance of 1 m from each other. The employees which are nominated for the position of 'Best Employee of the year' are seated at points A, B, C and D.
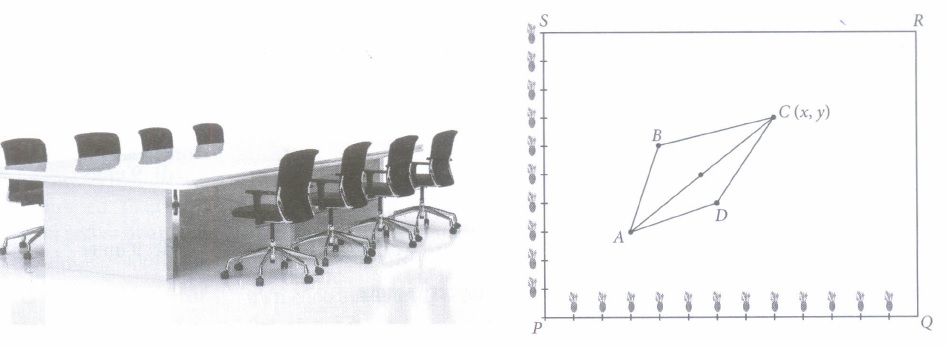
If P is considered as origin, then answer the following questions.
(i) The coordinates of A are(a) (2,2) (b) (3,3) (c) (4,4) (d) (5,5) (ii) The mid point of the line segment joining A and C is
(a) (5,5.5) (b) (5.7,7) (c) (5.5, 5) (d) None of these (iii) Which of the following is near to A?
(a) B (b) D (c) C (d) Both (a) and (b) (iv) Which of the following is equidistant from Band D?
(a) Only A (b) Only C (c) Both A and C (d) Neither A nor C (v) If Q is considered as origin, then the coordinates of D will be
(a) (-7,4) (b) (6,4) (c) (-4,7) (d) (4,6) (a) -
According to medical science and research, keeping an aquarium in the house helps in treating stress, anxiety and health problems associated with blood pressure. It also provides visual stimulation that boost your focus and creativity. A sketch of an aquarium is drawn, which is given in the following figure.

Considering P as origin, answer the following questions.
(i) The coordinates of H are(a) (4,2) (b) (4,3) (c) (2,4) (d) (4,8) (ii) Distance of the point G from the y-axis is
(a) 3 units (b) 4 units (c) 5 units (d) 9 units (iii) Length of side HG =
(a) 6 units (b) 7 units (c) 8 units (d) 9 units (iv) The length of diagonal FD and the value of x, respectively are
(a) 8 units,4 (b) \(\sqrt{8}\) units,5 (c) \(\sqrt{15}\) units,9 (d) \(\sqrt{61}\) units,9 (v) If Q is considered as origin, then the coordinates of mid-point of BC are
(a) (-1,4) (b) (1,6) (c) (6,1) (d) (6,-1) (a) -
Three friends Nitin, Alok and Deepika lives in societies represented by the points A, B and C respectively. They all work in the same office located at O. If they decided to share a cab to go to the office, then answer the following questions.
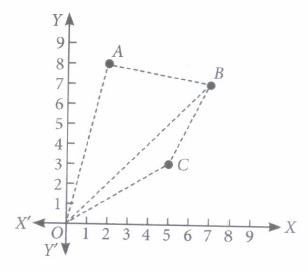
(I) Which society is nearest to the office?(a) A (b) B (c) C (d) Both A and C (ii) What is the distance between A and C?
(a) \(\sqrt{33}\) units (b) \(\sqrt{34}\)units (c) \(\sqrt{48}\) units (d) none of these (iii) Which of the following distance is least?
(a) AB (b) OA (c) BC (d) none of these (iv) Which of the following is the best route to go to the office?
(a) CABO (b) CBAO (c) ABCO (d) All of these (v) If Alok and Deepika planned to meet at a mall situated at a point D represented by the mid-point of the line joining the points Band C, then find the coordinates of D.
(a) (2,6) (b) (6,5) (c) (5,3) (d) (6,4) (a) -
To conduct Sports Day activities, in your rectangular shaped school ground ABCD, lines have been drawn with chalk powder at a distance of 1m each. 100 flower pots have been placed at a distance of 1m from each other along AD, as shown in the below figure. Niharika runs 1/4 th the distance AD on the 2nd line and posts a green flag. Preet runs 1/5 th the distance AD on the eighth line and posts a red flag.
(a) At what distance Niharika posted the green flag from the starting point of second line?(i) 20m (ii) 25 m (iii) 100 m (iv) 50 m (b) At what distance Preet posted the green flag from the starting point of eighth line?
(i) 20 m (ii) 25m (iii) 100m (iv) 50 m (c) What is the distance between both the flags?
(i) \(\sqrt{6} 1 \mathrm{~m}\) (ii) \(\sqrt{101}\) (iii) \(\sqrt{5} 1 \mathrm{~m}\) (iv) \(\sqrt{11} \mathrm{~m}\) (d) If Rashmi has to post a blue flag exactly halfway between the line segments joining the two flags, where should she post her flag?
(i) (5, 5) (ii) (22.5, 5) (iii) (5, 22.5) (iv) none of these (e) If Shweta has to post a white flag exactly halfway between the line segments joining A and red flag, where should she post her flag?
(i) (1, 5) (ii) (12.5, 1) (iii) (1, 22.5) (iv) (1, 12.5) (a)
Case Study
*****************************************
Answers
Coordinate Geometry Case Study Questions With Answer Key Answer Keys
-
(i) (a): Here, CD = \(\sqrt{(7-3)^{2}+(7-4)^{2}}\)
\(=\sqrt{4^{2}+3^{2}}\) = 5 units
Also, it is given that CE = 10 units
Thus, DE = CE - CD = 10 - 5 = 5 units (\(\because\) A, B, C, E are a line)
(ii) (b): Since, CD = DE = 5 units
\(\therefore\) Dis the midpoint of CE.
\(\therefore \quad \frac{x+3}{2}=7 \text { and } \frac{y+4}{2}=7 \)
\(\Rightarrow \quad x=11 \text { and } y=10 \Rightarrow x+y=21\)
(iii) (b)
(iv) (d): Let B divides AC in the ratio k:1, then
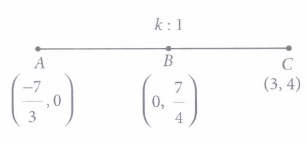
\(\frac{7}{4}=\frac{4 k+0}{k+1} \)
\(\Rightarrow 7 k+7=16 k \)
\(\Rightarrow 7=9 k \)
\(\Rightarrow k=\frac{7}{9}\)
Thus, the required ratio is 7 : 9
(v) (c): It can be easily verify that all the given points lie on the line represented by 3x - 4y + 7 = 0. -
(i) (d): Since the coordinates of A and Bare (2, 3) and (2, 1) respectively.
\(\therefore\) Required distance = AB
\(=\sqrt{(2-2)^{2}+(1-3)^{2}}=\sqrt{2^{2}}=2 \text { units }\)
(ii) (b): Since, library is situated at C(4, 1)
\(\therefore\)Required distance = BC
\(=\sqrt{(4-2)^{2}+(1-1)^{2}}=\sqrt{2^{2}+0^{2}}=2 \text { units }\)
(iii) (d): Required distance = AC
\(=\sqrt{(4-2)^{2}+(1-3)^{2}}=\sqrt{2^{2}+2^{2}}=2 \sqrt{2} \text { units }\)
(iv) (b): Since AB = BC \(\neq\) AC, therefore \(\Delta\)ABC is an isosceles triangle.
(v) (d): Distance between O and A
\(=\sqrt{2^{2}+3^{2}}=\sqrt{4+9}=\sqrt{13} \text { units }\)
and distance between O and B =
\(\sqrt{2^{2}+1^{2}}=\sqrt{4+1}=\sqrt{5} \text { units }\)
Thus, required distance = \((\sqrt{13}-\sqrt{5}) \text { units }\) -
(i) (a): We have, OA = 2\(\sqrt{2}\) km
\(\Rightarrow \sqrt{2^{2}+y^{2}}=2 \sqrt{2} \)
\(\Rightarrow 4+y^{2}=8 \Rightarrow y^{2}=4 \)
\(\Rightarrow y=2 \quad(\because y=-2 \text { is not possible })\)
(ii) (c): We have OB = 8\(\sqrt{2}\)
\(\Rightarrow \sqrt{x^{2}+8^{2}}=8 \sqrt{2} \)
\(\Rightarrow x^{2}+64=128 \Rightarrow x^{2}=64 \)
\(\Rightarrow x=8 \quad(\because x=-8 \text { is not possible })\)
(iii) (c) : Coordinates of A and Bare (2, 2) and (8, 8) respectively, therefore coordinates of point M are
\(\left(\frac{2+8}{2}, \frac{2+8}{2}\right)\)i.e .,(5.5)
(iv) (d): Let A divides OM in the ratio k: 1.Then
\(2=\frac{5 k+0}{k+1} \Rightarrow 2 \mathrm{k}+2=5 k \Rightarrow 3 k=2 \Rightarrow k=\frac{2}{3}\)
\(\therefore\) Required ratio = 2 : 3
(v) (b): Since M is the mid-point of A and B therefore AM = MB. Hence, he should try his luck moving towards B. -
Consider the house is at origin (0, 0), then coordinates of grocery store, electrician's shop, food cart and bus stand are respectively (2, 3), (-4, -6), (6, - 8) and (-6, 8)
(i) (d): Since, grocery store is at (2, 3) and food cart is at (6, -8)
\(\therefore\) Required distance \(=\sqrt{(6-2)^{2}+(-8-3)^{2}}\)
\(=\sqrt{4^{2}+11^{2}}=\sqrt{16+121}=\sqrt{137} \mathrm{~cm}\)
(ii) (b): Required distance
\(=\sqrt{(-6)^{2}+8^{2}}=\sqrt{36+64}=\sqrt{100}=10 \mathrm{~cm}\)
(iii) (c) : Let 0divides EG in the ratio k : I,then
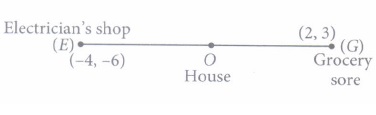
\(\begin{array}{l} 0=\frac{2 k-4}{k+1} \\ \Rightarrow \quad 2 k=4 \\ \Rightarrow k=2 \end{array}\)
Thus, 0 divides EG in the ratio 2 : 1
Hence, required ratio = OG :OE i.e., 1 : 2
(iv) (c): Since, (0, 0) is the mid-point of (-6,8) and (6, -8), therefore both bus stand and food cart are at equal distances from the house. Hence, required ratio is 1 : 1.
(v) (d): Mid-point of grocery store and electrician's shop is \(\left(\frac{2-4}{2}, \frac{3-6}{2}\right), \text { i.e., }\left(-1, \frac{-3}{2}\right)\) Thus, the diagonals does not bisect each other [\(\because\) Mid-point are not same]
Hence, they form a quadrilateral. -
(i) (c): Required coordinates are \(\left(0, \frac{4}{3}\right)\)
(ii) (c)
(iii) (a): Radius = Distance between (0,0) and \(\left(\frac{4}{3}, 0\right)\)
\(=\sqrt{\left(\frac{4}{3}\right)^{2}+0^{2}}=\frac{4}{3} \text { units }\)
(iv) (b): Area of circle = \(\pi\)(radius)2
\(=\pi\left(\frac{4}{3}\right)^{2}=\frac{16}{9} \pi \text { sq. units }\)
(v) (d): Let the coordinates of the other end be (x,y).
Then (0,0) will bethe mid-point of \(\left(1, \frac{\sqrt{7}}{3}\right)\) and (x, y).
\(\therefore\left(\frac{1+x}{2}, \frac{\frac{\sqrt{7}}{3}+y}{2}\right)=(0,0) \)
\(\Rightarrow \frac{1+x}{2}=0 \text { and } \frac{\frac{\sqrt{7}}{3}+y}{2}=0 \)
\(\Rightarrow x=-1 \text { and } y=-\frac{\sqrt{7}}{3}\)
Thus, the coordinates of other end be \(\left(-1, \frac{-\sqrt{7}}{3}\right)\) -
(i) (c): We have, P( -3,4), Q(3, 4) and R( -2, -1).
\(\therefore\) Coordinates of centroid of \(\Delta\)PQR
\(=\left(\frac{-3+3-2}{3}, \frac{4+4-1}{3}\right)=\left(\frac{-2}{3}, \frac{7}{3}\right)\)
(ii) (d): Coordinates of S= \(\left(\frac{-3+3}{2}, \frac{4+4}{2}\right)=(0,4)\)
(iii) (c): Coordinates of T= \(\left(\frac{-2+3}{2}, \frac{-1+4}{2}\right)=\left(\frac{1}{2}, \frac{3}{2}\right)\)
(iv) (a): Coordinates of U = \(\left(\frac{-2-3}{2}, \frac{-1+4}{2}\right)=\left(\frac{-5}{2}, \frac{3}{2}\right)\)
(v) (c): The centroid of triangle formed by joining the mid-points of sides of given triangle is same as that of the given trangle.
So, centroid of \(\Delta S T U=\left(\frac{-2}{3}, \frac{7}{3}\right)\) -
Coordinates of A, Band Care (-2, -3), (2, 3) and (3,2).
(i) (d): Required distance \(=\sqrt{(2+2)^{2}+(3+3)^{2}}\)
\(=\sqrt{4^{2}+6^{2}}=\sqrt{16+36}=2 \sqrt{13} \mathrm{~km} \approx 7.2 \mathrm{~km}\)
(ii) (d): Required distance \(=\sqrt{(3+2)^{2}+(2+3)^{2}}\)
\(=\sqrt{5^{2}+5^{2}}=5 \sqrt{2} \mathrm{~km}\)
(iii) (b): Distance between Band C
\(=\sqrt{(3-2)^{2}+(2-3)^{2}}=\sqrt{1+1}=\sqrt{2} \mathrm{~km}\)
Thus, distance travelled by first bus to reach to B
\(=A C+C B=5 \sqrt{2}+\sqrt{2}=6 \sqrt{2} \mathrm{~km} \approx 8.48 \mathrm{~km}\)
and distance travelled by second bus to reach to B
\(=A B=2 \sqrt{13} \mathrm{~km} \approx 7.2 \mathrm{~km}\)
\(\therefore\) Distance of first bus is greater than distance of the
second bus, therefore second bus should be chosen.
(iv) (d): Distance travelled by first bus = 8.48 km
\(\therefore\) Total fare = 8.48 x 10 = Rs 84.80
(v) (b): Distance travelled by second bus = 7. 2 km
\(\therefore\) Total fare = 7.2 x 15 = Rs 108
-
(i) (a): Since the diagonals of a parallelogram bisect each other.
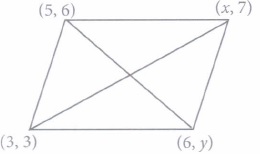
\(\therefore\) By mid-point formula, we have
\(\left(\frac{x+3}{2}, \frac{3+7}{2}\right)=\left(\frac{5+6}{2}, \frac{6+y}{2}\right) \)
\(\Rightarrow x+3=11 \text { and } y+6=10 \Rightarrow x=8 \text { and } y=4\)
(ii) (d): Distance between (3, 3) and (6, 4)
\(=\sqrt{(6-3)^{2}+(4-3)^{2}}=\sqrt{9+1}=\sqrt{10} \text { units }\)
And distance between (6, 4) and (8, 7)
\(=\sqrt{(8-6)^{2}+(7-4)^{2}}=\sqrt{4+9}=\sqrt{13} \text { units }\)
Now, required perimeter \(=2(\sqrt{10}+\sqrt{13}) \text { units }\)
(iii) (a): Let A(l, 3), B(2, 6), C(S, 7) and D(4, 4) be the given points. Then length of diagonal
\(A C =\sqrt{(5-1)^{2}+(7-3)^{2}=\sqrt{16+16}} \)
\(=\sqrt{32}=4 \sqrt{2} \text { units } \)
\(\text { and } B D =\sqrt{(4-2)^{2}+(4-6)^{2}}=\sqrt{4+4} \)
\(=\sqrt{8}=2 \sqrt{2} \text { units }\)
(iv) (d): Length of one of the sides
\(=\sqrt{(2-1)^{2}+(6-3)^{2}}=\sqrt{1+9}=\sqrt{10} \text { units }\)
\(\therefore \quad \text { Perimeter }=4 \sqrt{10} \text { units }\)
(v) (c) -
(i) (b): The distance between A and C
\(=\sqrt{(8-4)^{2}+(5+3)^{2}}=\sqrt{4^{2}+8^{2}} \)
\(=\sqrt{16+64}=\sqrt{80}=4 \sqrt{5} \text { units }\)
(ii) (a): Let the coordinates of I be (x, y).
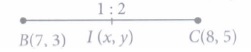
Then, by section formula
\(x =\frac{1 \times 8+2 \times 7}{1+2}=\frac{8+14}{3}=\frac{22}{3}\)
\(\text { and } y =\frac{1 \times 5+2 \times 3}{1+2}=\frac{5+6}{3}=\frac{11}{3}\)
Thus, the coordinates of I is \(\left(\frac{22}{3}, \frac{11}{3}\right)\)
(iii) (b): The mid -point of A and C
\(=\left(\frac{8+4}{2}, \frac{5-3}{2}\right)=(6,1)\)
(iv) (b): Let B divides the line segment joining A and C in the ratio k : 1. Then, the coordinates of B will be
\(\left(\frac{8 k+4}{k+1}, \frac{5 k-3}{k+1}\right)\)
\(\text { Thus, we have }\left(\frac{8 k+4}{k+1}, \frac{5 k-3}{k+1}\right)=(7,3)\)
\(\Rightarrow \frac{8 k+4}{k+1}=7 \text { and } \frac{5 k-3}{k+1}=3 \)
\(\text { Consider, } \frac{8 k+4}{k+1}=7 \Rightarrow 8 k+4=7 k+7 \Rightarrow k=3\)
Hence, the required ratio is 3 : 1
(v) (a):\(\because\) B divides AC in the ratio 3 : 4.
\(\therefore\) A, B, C lie on a straight line. -
(i) (c) :The coordinates of point A are (9, 27), therefore its distance from x-axis = 27 units.
(ii) (b): Coordinates of Band Care (4, 19) and (14, 19)
\(\therefore \quad \text { Required distance } =\sqrt{(14-4)^{2}+(19-19)^{2}} \)
\(=\sqrt{10^{2}}=10 \text { units }\)
(iii) (c) : Coordinates of F and G are (2, 6) and (16,6) respectively.
\(\therefore \quad \text { Required distance } =\sqrt{(16-2)^{2}+(6-6)^{2}}\)
\(=\sqrt{14^{2}}=14 \text { units } \)
(iv) (a): Since the coordinates of F and Care (2, 6) and (16, 6) respectively therefore mid-point of FG is
\(\left(\frac{2+16}{2}, \frac{6+6}{2}\right)=(9,6)\)
Thus, the mid-point of FC will lie on the line represented by x = 9.
(v) (d): Coordinates of Land N are (6,4) and (7, 1) respectively.
\(\text { Length of } L N =\sqrt{(7-6)^{2}+(1-4)^{2}} \)
\(=\sqrt{1+9}=\sqrt{10} \text { units }\)
\(\Rightarrow \text { Length of } M P=\sqrt{10} \text { units }\)
Now, perimeter of LMPN = LN + LM + MP + NP
\(=\sqrt{10}+6+\sqrt{10}+4=(2 \sqrt{10}+10) \text { units } \)
\({[\because L M=12-6=6 \text { units and } N P=11-7=4 \text { units }]}\) -
(i) (a): Coordinates of Q are (9, 5).
\(\therefore\) Distance of point Q from y-axis = 9 units
(ii) (b): Coordinates of point U are (8, 2).
(iii) (d): We have, P(2, 5) and Q (9, 5)
\(\therefore \quad P Q=\sqrt{(2-9)^{2}+(5-5)^{2}}=\sqrt{49+0}=7 \text { units }\)
(iv) (c): Point A(x, y) is equidistant from R (3, 8) and T(3,2).
\(\therefore \quad A R=A T \Rightarrow A R^{2}=A T^{2} \)
\(\Rightarrow \quad(x-3)^{2}+(y-8)^{2}=(x-3)^{2}+(y-2)^{2} \)
\(\Rightarrow y^{2}+64-16 y=y^{2}+4-4 y \)
\(\Rightarrow 16 y-4 y=64-4 \)
\(\Rightarrow 12 y=60 \Rightarrow y=5\)
(v) (d): Length of TU = 5 units and of TL = 2 units
\(\therefore\) Perimeter of image of a rectangular face = 2(5 + 2) = 14 units -
(i) (b): Clearly, coordinates of A are (3, 3).
(ii) (c): Coordinates of Care (8, 7) therefore midpoint of AC is

\(\left(\frac{3+8}{2}, \frac{3+7}{2}\right) \text { , i.e., }(5.5,5)\)
(iii) (d): Coordinates of Band Dare (4, 6) and (6,4), respectively.
Distance between A and B \(=\sqrt{(4-3)^{2}+(6-3)^{2}}\)
\(=\sqrt{1^{2}+3^{2}}=\sqrt{10}\)
and Distance between A and D \(=\sqrt{(6-3)^{2}+(4-3)^{2}}\)
\(=\sqrt{3^{2}+1^{2}}=\sqrt{10}\)
Thus, both Band D are near to A.
(iv) (a): Distance between Band C
\(=\sqrt{(8-4)^{2}+(7-6)^{2}}=\sqrt{16+1}=\sqrt{17}\)
Distance between D and C \(=\sqrt{(8-6)^{2}+(7-4)^{2}}\)
\(=\sqrt{4+9}=\sqrt{13}\)
(v) (a): When Q is taken as origin, then coordinates of D = (-7, 4) -
(i) (c): We are given that P is origin.
\(\therefore\) Coordinates of Hare (2,4).
(ii) (d): Coordinates of G are (9,4), therefore distance of G from y-axis = 9 units.
(iii) (b) : Coordinates of Hare (2, 4) and coordinates of G are (9, 4).
\(\text { Thus, } G H=\sqrt{(9-2)^{2}+(4-4)^{2}}=\sqrt{7^{2}+0}=7 \text { units }\)
(iv) (d): Coordinates of Dare (4,2) and coordinates of Fare (9, 8).
\(\Rightarrow\) x = 9
Also, length of diagonal FD \(=\sqrt{(4-9)^{2}+(2-8)^{2}}\)
\(=\sqrt{25+36}=\sqrt{61} \text { units }\)
(v) (a): If Q is origin, then Coordinates of Bare (-1,6) and of Care (-1,2).
Now, mid-point BC = \(\left(\frac{(-1)+(-1)}{2}, \frac{6+2}{2}\right) \text { i.e., }(-1,4)\) -
Coordinates of A, Band Care (2,8), (7, 7) and (5, 3) respectively.
(i) (c): From the graph, it is clear that C is nearest to the office.
(ii) (b): Distance between A and C
\(=\sqrt{(5-2)^{2}+(3-8)^{2}}=\sqrt{3^{2}+5^{2}}=\sqrt{9+25}=\sqrt{34} \text { units }\)
(iii) (c) : AB \(=\sqrt{(7-2)^{2}+(7-8)^{2}}=\sqrt{26} \text { units }\)
\(O A=\sqrt{2^{2}+8^{2}}=2 \sqrt{17} \text { units } \)
\(B C=\sqrt{(7-5)^{2}+(7-3)^{2}}=2 \sqrt{5} \text { units }\)
\(\therefore B C \text { is the least. }\)
(iv) (c)
(v) (b): Coordinates of D = \(\left(\frac{5+7}{2}, \frac{3+7}{2}\right)=(6,5)\) -
(a) (ii) Distance covered by Niharika
= Niharika runs \(\frac{1}{4}\) distance AD on the 2nd line
= \(\frac{1}{4} \times 100=25 \mathrm{~m}\)
(b) (i) Distance covered by Preet
= Preet runs \(\frac{1}{5}\) th distance AD on the 8 th line
= \(\frac{1}{5} \times 100=20 \mathrm{~m}\)
(c) (i) Distance between Green and Red flags
= \(\)\(\sqrt{(8-2)^{2}+(20-25)^{2}}\)
= \(\sqrt{36+25}=\sqrt{61} \mathrm{~m}\)
(d) (iii)Position of blue flag
= Mid-point of green flag and red flag
= \(\left(\frac{2+8}{2}, \frac{25+20}{2}\right)=(5,22.5)\)
(e) (iv) (1,12,5)

























