Class 10th Maths - Introduction to Trigonometry Case Study Questions and Answers 2022 - 2023
By QB365 on 09 Sep, 2022
QB365 provides a detailed and simple solution for every Possible Case Study Questions in Class 10th Maths Subject - Introduction to Trigonometry, CBSE. It will help Students to get more practice questions, Students can Practice these question papers in addition to score best marks.
QB365 - Question Bank Software
Introduction to Trigonometry Case Study Questions With Answer Key
10th Standard CBSE
-
Reg.No. :
Maths
-
Three friends - Anshu, Vijay and Vishal are playing hide and seek in a park. Anshu and Vijay hide in the shrubs and Vishal have to find both of them. If the positions of three friends are at A, Band C respectively as shown in the figure and forms a right angled triangle such that AB = 9 m, BC = 3\(\sqrt{3}\) m and \(\angle\)B = 90°, then answer the following questions.

(i) The measure of \(\angle\)A is(a) 30° (b) 45° (c) 60° (d) None of these (ii) The measure of \(\angle\)C is
(a) 30° (b) 45° (c) 60° (d) None of these (iii) The length of AC is
\((a) 2 \sqrt{3} \mathrm{~m}\) \((b) \sqrt{3} \mathrm{~m}\) \((c) 4 \sqrt{3} \mathrm{~m}\) \((d) 6 \sqrt{3} \mathrm{~m}\) (iv) cos2A =
(a) 0 \((b) \frac{1}{2}\) \((c) \frac{1}{\sqrt{2}}\) \((d) \frac{\sqrt{3}}{2}\) (v) sin \(\left(\frac{C}{2}\right)\) =
(a) 0 \((b) \frac{1}{2}\) \((c) \frac{1}{\sqrt{2}}\) \((d) \frac{\sqrt{3}}{2}\) (a) -
Two aeroplanes leave an airport, one after the other. After moving on runway, one flies due North and other flies due South. The speed of two aeroplanes is 400 km/hr and 500 km/hr respectively. Considering PQ as runway and A and B are any two points in the path followed by two planes, then answer the following questions.

(i) Find \(\tan \theta ; \text { if } \angle A P Q=\theta\)\((a) \frac{1}{2}\) \((b) \frac{1}{\sqrt{2}}\) \((c) \frac{\sqrt{3}}{2}\) \((d) \frac{3}{4}\) (ii) Find cot B
\((a) \frac{3}{4}\) \((b) \frac{15}{4}\) \((c) \frac{3}{8}\) \((d) \frac{15}{8}\) (iii) Find tanA.
\((a) 2\) \((b) \sqrt{2}\) \((c) \frac{4}{3}\) \((d) \frac{2}{\sqrt{3}}\) (iv) Find secA.
\((a) 1\) \((b) \frac{2}{3}\) \((c) \frac{4}{3}\) \((d) \frac{5}{3}\) (v) Find cosecB.
\((a) \frac{17}{8}\) \((b) \frac{12}{5}\) \((c) \frac{5}{12}\) \((d) \frac{8}{17}\) (a) -
Anita, a student of class 10th, has to made a project on 'Introduction to Trigonometry' She decides to make a bird house which is triangular in shape. She uses cardboard to make the bird house as shown in the figure. Considering the front side of bird house as right angled triangle PQR, right angled at R, answer the following questions.
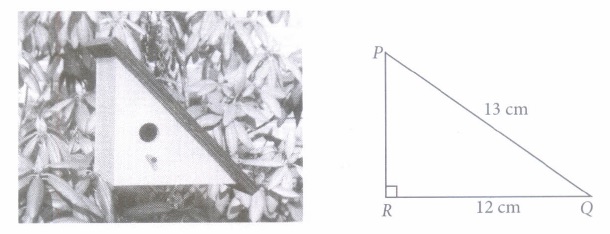
(i) If \(\angle P Q R=\theta, \text { then } \cos \theta=\)\((a) \frac{12}{5}\) \((b) \frac{5}{12}\) \((c) \frac{12}{13}\) \((d) \frac{13}{12}\) (ii) The value of sec \(\theta\) =
\((a) \frac{5}{12}\) \((b) \frac{12}{5}\) \((c) \frac{13}{12}\) \((d) \frac{12}{13}\) (iii) The value of \(\frac{\tan \theta}{1+\tan ^{2} \theta}=\)
\((a) \frac{5}{12}\) \((b) \frac{12}{5}\) \((c) \frac{60}{169}\) \((d) \frac{169}{60}\) (iv) The value of \(\cot ^{2} \theta-\operatorname{cosec}^{2} \theta=\)
(a) -1 (b) 0 (c) 1 (d) 2 (v) The value of \(\sin ^{2} \theta+\cos ^{2} \theta=\)
(a) 0 (b) 1 (c) -1 (d) 2 (a) -
Ritu's daughter is feeling so hungry and so thought to eat something. She looked into the fridge and found some bread pieces. She decided to make a sandwich. She cut the piece of bread diagonally and found that it forms a
righ.t angled triangle with sides 4 cm, 4\(\sqrt{3}\) cm and 8 cm.

On the basis of above information, answer the following questions.
(i) The value of \(\angle\)M =(a) 30° (b) 60° (c) 45° (d) None of these (ii) The value of \(\angle\)K =
(a) 45° (b) 30 ° (c) 60° (d) None of these (iii) Find the value of tanM.
\((a) \sqrt{3}\) \((b) \frac{1}{\sqrt{3}}\) (c) 1 (d) None of these (iv) sec2M - 1 =
(a) tanM (b) tan2M (c) tan2M (d) None of these (v) The value of \(\frac{\tan ^{2} 45^{\circ}-1}{\tan ^{2} 45^{\circ}+1}\) is
(a) 0 (b) 1 (c) 2 (d) -1 (a) -
Aanya and her father go to meet her friend Juhi for a party. When they reached to [uhi's place, Aanya saw the roof of the house, which is triangular in shape. If she imagined the dimensions of the roof as given in the figure, then answer the following questions.
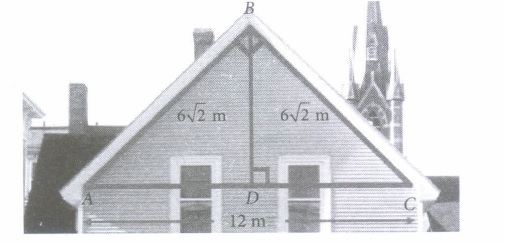
(i) If D is the mid point of AC, then BD =(a) 2m (b) 3m (c) 4m (d) 6m (ii) Measure of \(\angle\)A =
(a) 30° (b) 60° (c) 45° (d) None of these (iii) Measure of \(\angle\)C =
(a) 30° (b) 60° (c) 45° (d) None of these (iv) Find the value of sinA + cosC.
(a) 0 (b) 1 (c) \(\frac{1}{2}\) (d) \(\sqrt{2}\) (v) Find the value of tan2C + tan2 A.
(a) 0 (b) 1 (c) 2 (d) \(\frac{1}{2}\) (a)
Case Study
*****************************************
Answers
Introduction to Trigonometry Case Study Questions With Answer Key Answer Keys
-
(i) (a): We have, AB = 9 m, BC = 3\(\sqrt{3}\) m
In \(\Delta\)ABC, we have
\(\tan A=\frac{B C}{A B}=\frac{3 \sqrt{3}}{9}=\frac{1}{\sqrt{3}} \)
\(\Rightarrow \tan A=\tan 30^{\circ} \Rightarrow \angle A=30^{\circ}\)
(ii) (c): Similarly, \(\tan C=\frac{A B}{B C}=\frac{9}{3 \sqrt{3}}=\sqrt{3}\)
\(\Rightarrow \tan C=\tan 60^{\circ} \Rightarrow \angle C=60^{\circ}\)
(iii) (d): Since \(\sin A=\frac{B C}{A C} \Rightarrow \sin 30^{\circ}=\frac{B C}{A C}\)
\(\Rightarrow \frac{1}{2}=\frac{3 \sqrt{3}}{A C} \Rightarrow A C=6 \sqrt{3} \mathrm{~m}\)
(iv) (b) : \(\because \angle A=30^{\circ}\) [From (1)]
\(\therefore \quad \cos 2 A=\cos \left(2 \times 30^{\circ}\right)=\cos 60^{\circ}=\frac{1}{2}\)
(v) (b): \(\because \angle C=60^{\circ}\) [Using (2)]
\(\therefore \quad \sin \left(\frac{C}{2}\right)=\sin \left(\frac{60^{\circ}}{2}\right)=\sin 30^{\circ}=\frac{1}{2}\) -
(i) (d) : \(\text { In } \Delta A P Q, \tan \theta=\frac{A Q}{P Q}=\frac{1.2}{1.6}=\frac{3}{4}\)
(ii) (d) : \(\text { In } \Delta P B Q, \cot B=\frac{Q B}{P Q}=\frac{3}{1.6}=\frac{15}{8}\) ...(i)
(iii) (c): \(\text { In } \Delta A P Q, \tan A=\frac{P Q}{A Q}=\frac{1.6}{1.2}=\frac{4}{3}\) ...(ii)
(iv) (d): We have, tan2A + 1 = sec2A
\(\Rightarrow \sec A =\sqrt{\left(\frac{4}{3}\right)^{2}+1} \)
\(=\sqrt{\frac{16}{9}+1}=\sqrt{\frac{25}{9}}=\frac{5}{3}\)
(v) (a): Since \(\operatorname{cosec} B=\sqrt{\cot ^{2} B+1}\)
\(\begin{array}{l} =\sqrt{\left(\frac{15}{8}\right)^{2}+1} \\ =\frac{17}{8} \end{array}\) -
\(\because \Delta\)PQR is a right angled triangle.
\(\therefore\) PR2 + RQ2 = PQ2
\(\Rightarrow P R^{2}=(13)^{2}-(12)^{2}=25 \Rightarrow P R=5 \mathrm{~cm}\)
(i) (c) : \(\cos \theta=\frac{Q R}{P Q}=\frac{12}{13} \)
(ii) (c) : \(\sec \theta=\frac{1}{\cos \theta}=\frac{13}{12} \)
(iii) (c) : \(\tan \theta=\frac{P R}{R Q}=\frac{5}{12}\)
\(\therefore \frac{\tan \theta}{1+\tan ^{2} \theta}=\frac{\frac{5}{12}}{1+\frac{25}{144}}=\frac{\frac{5}{12}}{\frac{169}{144}}=\frac{60}{169}\)
(iv) (a): \(\cot \theta=\frac{1}{\tan \theta}=\frac{12}{5}\) [Using (1)]
\(\operatorname{cosec} \theta=\frac{P Q}{P R}=\frac{13}{5} \)
\(\therefore \quad \cot ^{2} \theta-\operatorname{cosec}^{2} \theta=\frac{144}{25}-\frac{169}{25}=-1\)
(v) (b): \(\sin ^{2} \theta+\cos ^{2} \theta=1\) (Using identity) -
We have, KL = 4 cm, ML = 4\(\sqrt{3}\)m, KM = 8 cm
(i) (a): \(\tan M=\frac{K L}{L M}=\frac{4}{4 \sqrt{3}}=\frac{1}{\sqrt{3}}\)
\(\Rightarrow \tan M=\tan 30^{\circ} \Rightarrow \angle M=30^{\circ}\)
(ii) (c) : \(\tan K=\frac{M L}{K L}=\frac{4 \sqrt{3}}{4}=\sqrt{3}=\tan 60^{\circ}\)
\(\Rightarrow \angle K=60^{\circ}\)
(iii) (b)
(iv) (c)
(v) (a) : \(\frac{\tan ^{2} 45^{\circ}-1}{\tan ^{2} 45^{\circ}+1}=\frac{(1)^{2}-1}{1^{2}+1}=\frac{0}{2}=0\) -
We have, AB = BC = 6\(\sqrt{2}\) m and AC=12m .
(i) (d):\(\because\) Dis mid point of AC.
\(\therefore\) AD=DC=6m
Now, AB2 = BD2 + AD2 (\(\therefore\) \(\Delta\)ABD is a right triangle)
\(\Rightarrow B D^{2}=(6 \sqrt{2})^{2}-6^{2}=72-36=36 \)
\(\Rightarrow B D=6 \mathrm{~m}\)
(ii) (c) : \(\operatorname{In} \Delta A B D, \sin A=\frac{B D}{A B}=\frac{6}{6 \sqrt{2}}=\frac{1}{\sqrt{2}}\)
\(\Rightarrow \sin A=\sin 45^{\circ} \Rightarrow \angle A=45^{\circ}\)
(iii) (c) : \(\operatorname{In} \Delta B D C, \tan C=\frac{B D}{D C}=\frac{6}{6}\)
\(\Rightarrow \tan C=1=\tan 45^{\circ} \Rightarrow \angle C=45^{\circ}\)
(iv) (d) : \(\sin A=\frac{1}{\sqrt{2}}, \cos C=\cos 45^{\circ}=\frac{1}{\sqrt{2}}\)
\(\therefore \quad \sin A+\cos C=\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}=\frac{2}{\sqrt{2}}=\sqrt{2}\)
(v) (c): \((v) \quad(c): \tan C=1, \tan A=\tan 45^{\circ}=1\)
\(\Rightarrow \tan ^{2} C+\tan ^{2} A=1+1=2\)

























