Class 10th Maths - Probability Case Study Questions and Answers 2022 - 2023
By QB365 on 09 Sep, 2022
QB365 provides a detailed and simple solution for every Possible Case Study Questions in Class 10th Maths Subject - Probability, CBSE. It will help Students to get more practice questions, Students can Practice these question papers in addition to score best marks.
QB365 - Question Bank Software
Probability Case Study Questions With Answer Key
10th Standard CBSE
-
Reg.No. :
Maths
-
Two friends Richa and Sohan have some savings in their piggy bank. They decided to count the total coins they both had. After counting they find that they have fifty \(\begin{equation} ₹ \end{equation} \) 1 coins, forty eight \(\begin{equation} ₹ \end{equation} \) 2 coins, thirty six \(\begin{equation} ₹ \end{equation} \) 5 coins, twenty eight \(\begin{equation} ₹ \end{equation} \)10 coins and eight \(\begin{equation} ₹ \end{equation} \) 20 coins. Now, they said to Nisha, their another friends, to choose a coin randomly.
Find the probability that the coin chosen is

(i) \(\begin{equation} ₹ \end{equation} \)5 coin(a) \(\begin{equation} \frac{17}{55} \end{equation}\) (b) \(\begin{equation} \frac{36}{85} \end{equation}\) (c) \(\begin{equation} \frac{18}{85} \end{equation}\) (d) \(\begin{equation} \frac{1}{15} \end{equation}\) (ii) \(\begin{equation} ₹ \end{equation} \) 20 coin
(a) \(\begin{equation} \frac{13}{85} \end{equation}\) (b) \(\begin{equation} \frac{4}{85} \end{equation}\) (c) \(\begin{equation} \frac{3}{85} \end{equation}\) (d) \(\begin{equation} \frac{4}{15} \end{equation}\) (iii) not a \(\begin{equation} ₹ \end{equation} \) 10 coin
(a) \(\begin{equation} \frac{15}{31} \end{equation}\) (b) \(\begin{equation} \frac{36}{85} \end{equation}\) (c) \(\begin{equation} \frac{1}{5} \end{equation}\) (d) \(\begin{equation} \frac{71}{85} \end{equation}\) (iv) of denomination of atleast \(\begin{equation} ₹ \end{equation} \)10.
(a) \(\begin{equation} \frac{18}{85} \end{equation}\) (b) \(\begin{equation} \frac{36}{85} \end{equation}\) (c) \(\begin{equation} \frac{1}{17} \end{equation}\) (d) \(\begin{equation} \frac{16}{85} \end{equation}\) (v) of denomination of atmost \(\begin{equation} ₹ \end{equation} \) 5.
(a) \(\begin{equation} \frac{67}{85} \end{equation}\) (b) \(\begin{equation} \frac{36}{85} \end{equation}\) (c) \(\begin{equation} \frac{4}{85} \end{equation}\) (d) \(\begin{equation} \frac{18}{85} \end{equation}\) (a) -
In a play zone, Nishtha is playing claw crane game which consists of 58 teddy bears, 42 pokemons, 36 tigers and 64 monkeys. Nishtha picks a puppet at random. Now, find the probability of getting

(i) a tiger(a) \(\begin{equation} \frac{3}{50} \end{equation}\) (b) \(\begin{equation} \frac{9}{50} \end{equation}\) (c) \(\begin{equation} \frac{1}{25} \end{equation}\) (d) \(\begin{equation} \frac{27}{50} \end{equation}\) (ii) a monkey
(a) \(\begin{equation} \frac{8}{25} \end{equation}\) (b) \(\begin{equation} \frac{4}{25} \end{equation}\) (c) \(\begin{equation} \frac{16}{25} \end{equation}\) (d) \(\begin{equation} \frac{1}{5} \end{equation}\) (iii) a teddy bear
(a) \(\begin{equation} \frac{41}{50} \end{equation}\) (b) \(\begin{equation} \frac{29}{50} \end{equation}\) (c) \(\begin{equation} \frac{29}{100} \end{equation}\) (d) \(\begin{equation} \frac{41}{100} \end{equation}\) (iv) not a monkey
(a) \(\begin{equation} \frac{1}{25} \end{equation}\) (b) \(\begin{equation} \frac{8}{25} \end{equation}\) (c) \(\begin{equation} \frac{13}{25} \end{equation}\) (d) \(\begin{equation} \frac{17}{25} \end{equation}\) (v) not a pokemon
(a) \(\begin{equation} \frac{27}{100} \end{equation}\) (b) \(\begin{equation} \frac{43}{100} \end{equation}\) (c) \(\begin{equation} \frac{61}{100} \end{equation}\) (d) \(\begin{equation} \frac{79}{100} \end{equation}\) (a) -
Rohit wants to distribute chocolates in his class on his birthday. The chocolates are of three types: Milk chocolate, White chocolate and Dark chocolate. If the total number of students in the class is 54 and everyone gets a chocolate, then answer the following questions.

(i) If the probability of distributing milk chocolates is 1/3, then the number of milk chocolates Rohit has, is(a) 18 (b) 20 (c) 22 (d) 30 (ii) If the probability of distributing dark chocolates is 4/9, then the number of dark chocolates Rohit has, is
(a) 18 (b) 25 (c) 24 (d) 36 (iii) The probability of distributing white chocolates is
(a) \(\begin{equation} \frac{11}{27} \end{equation}\) (b)\(\begin{equation} \frac{8}{21} \end{equation}\) (c) \(\begin{equation} \frac{1}{9} \end{equation}\) (d) \(\begin{equation} \frac{2}{9} \end{equation}\)
(iv) The probability of distributing both milk and white chocolates is(a) \(\begin{equation} \frac{3}{17} \end{equation}\) (b) \(\begin{equation} \frac{5}{9} \end{equation}\) (c) \(\begin{equation} \frac{1}{3} \end{equation}\) (d) \(\begin{equation} \frac{1}{27} \end{equation}\) (v) The probability of distributing all the chocolates is
(a) 0 (b) 1 (c) \(\begin{equation} \frac{1}{2} \end{equation}\) (d) \(\begin{equation} \frac{3}{4} \end{equation}\) (a) -
In a party, some children decided to play musical chair game. In the game the person playing the music has been advised to stop the music at any time in the interval of 3 mins after he start the music in each turn. On the basis of the given information, answer the following questions.
(i) What is the probability that the music will stop within first 30 sees after starting?(a) \(\begin{equation} \frac{1}{6} \end{equation}\) (b) \(\begin{equation} \frac{1}{5} \end{equation}\) (c) \(\begin{equation} \frac{1}{4} \end{equation}\) (d) \(\begin{equation} \frac{1}{3} \end{equation}\) (ii) The probability that the music will stop within 45 sees after starting is
(a) \(\begin{equation} \frac{1}{4} \end{equation}\) (b) \(\begin{equation} \frac{1}{5} \end{equation}\) (c) \(\begin{equation} \frac{1}{6} \end{equation}\) (d) \(\begin{equation} \frac{1}{8} \end{equation}\) (iii) The probability that the music will stop after 2 mins after starting is
(a) \(\begin{equation} \frac{1}{8} \end{equation}\) (b) \(\begin{equation} \frac{1}{5} \end{equation}\) (c) \(\begin{equation} \frac{1}{4} \end{equation}\) (d) \(\begin{equation} \frac{1}{3} \end{equation}\) (iv) The probability that the music will not stop within first 60 sees after starting is
(a) \(\begin{equation} \frac{1}{3} \end{equation}\) (b) \(\begin{equation} \frac{2}{3} \end{equation}\) (c) \(\begin{equation} \frac{4}{5} \end{equation}\) (d) \(\begin{equation} \frac{8}{9} \end{equation}\) (v) The probability that the music will stop within first 82 sees after starting is
(a) \(\begin{equation} \frac{11}{30} \end{equation}\) (b) \(\begin{equation} \frac{41}{90} \end{equation}\) (c) \(\begin{equation} \frac{31}{35} \end{equation}\) (d) \(\begin{equation} \frac{41}{93} \end{equation}\) (a) -
Three persons toss 3 coins simultaneously and note the outcomes. Then, they ask few questions to one another. Help them in finding the answers of the following questions.

(i) The probability of getting atmost one tail is(a) 0 (b) 1 (c) \(\begin{equation} \frac{1}{2} \end{equation}\) (d) \(\begin{equation} \frac{1}{4} \end{equation}\) (ii) The probability of getting exactly 1 head is
(a) \(\begin{equation} \frac{1}{2} \end{equation}\) (b) \(\begin{equation} \frac{1}{4} \end{equation}\) (c) \(\begin{equation} \frac{1}{8} \end{equation}\) (d) \(\begin{equation} \frac{3}{8} \end{equation}\) (iii) The probability of getting exactly 3 tails is
(a) 0 (b) 1 (c) \(\begin{equation} \frac{1}{4} \end{equation}\) (d) \(\begin{equation} \frac{1}{8} \end{equation}\) (iv) The probability of getting atmost 3 heads is
(a) 0 (b) 1 (c) \(\begin{equation} \frac{1}{2} \end{equation}\) (d) \(\begin{equation} \frac{1}{8} \end{equation}\) (v) The probability of getting atleast two heads is
(a) 0 (b) 1 (c) \(\begin{equation} \frac{1}{2} \end{equation}\) (d) \(\begin{equation} \frac{1}{4} \end{equation}\) (a) -
Prateek goes to a toy shop to purchase a building block kit for his son. He found that the kit contains 120 blocks, of which 40 are red, 25 are blue, 30 are green and the rest are yellow. His son picks up a block at random. Find the probability that the block is

(i) of red colour(a) 0 (b) 1 (c) \(\begin{equation} \frac{1}{2} \end{equation}\) (d) \(\begin{equation} \frac{1}{3} \end{equation}\) (ii) not of yellow colour
(a) \(\begin{equation} \frac{1}{6} \end{equation}\) (b) \(\begin{equation} \frac{1}{4} \end{equation}\) (c) \(\begin{equation} \frac{19}{24} \end{equation}\) (d) \(\begin{equation} \frac{19}{25} \end{equation}\) (iii) of green colour
(a) \(\begin{equation} \frac{1}{8} \end{equation}\) (b) \(\begin{equation} \frac{1}{10} \end{equation}\) (c) \(\begin{equation} \frac{1}{4} \end{equation}\) (d) \(\begin{equation} \frac{1}{12} \end{equation}\) (iv) of yellow colour
(a) \(\begin{equation} \frac{15}{118} \end{equation}\) (b) \(\begin{equation} \frac{5}{24} \end{equation}\) (c) \(\begin{equation} \frac{17}{24} \end{equation}\) (d) \(\begin{equation} \frac{19}{50} \end{equation}\) (v) not of blue colour
(a) \(\begin{equation} \frac{1}{8} \end{equation}\) (b) \(\begin{equation} \frac{19}{24} \end{equation}\) (c) \(\begin{equation} \frac{19}{31} \end{equation}\) (d) \(\begin{equation} \frac{16}{55} \end{equation}\) (a) -
Rahul goes to a fete in Mussoorie. There he saw a game having prizes - wall clocks, power banks, puppets and water bottles. The game consists of a box having cards inside it, bearing the numbers 1 to 200, one on each card.
A person has to select a card at random. Now, the winning of prizes has the following conditions:- Wall clock - If the number on the selected card is a perfect square.
- Power bank - If the number on the selected card is multiple of 3.
- Puppet - If the number on selected card is divisible by 10.
- Water bottle - If the number on the selected card is a prime number more than 100 but less than 150.
- Better luck next time - If the number on the selected card is a perfect cube.

On the basis of above information, answer the following questions.
(i) Find the probability of winning a puppet.(a) \(\begin{equation} \frac{1}{5} \end{equation}\) (b) \(\begin{equation} \frac{1}{8} \end{equation}\) (c) \(\begin{equation} \frac{1}{10} \end{equation}\) (d) \(\begin{equation} \frac{2}{15} \end{equation}\) (ii) The probability of winning a water bottle is
(a) \(\begin{equation} \frac{1}{18} \end{equation}\) (b) \(\begin{equation} \frac{1}{19} \end{equation}\) (c) \(\begin{equation} \frac{1}{20} \end{equation}\) (d) \(\begin{equation} \frac{1}{16} \end{equation}\) (iii) The probability of winning a power bank is
(a) \(\begin{equation} \frac{3}{10} \end{equation}\) (b) \(\begin{equation} \frac{11}{50} \end{equation}\) (c) \(\begin{equation} \frac{33}{100} \end{equation}\) (d) \(\begin{equation} \frac{1}{8} \end{equation}\) (iv) The probability of winning a wall clock is
(a) \(\begin{equation} \frac{7}{100} \end{equation}\) (b) \(\begin{equation} \frac{51}{100} \end{equation}\) (c) \(\begin{equation} \frac{19}{100} \end{equation}\) (d) \(\begin{equation} \frac{27}{100} \end{equation}\) (v) The probability of getting 'Better Luck next time' is
(a) \(\begin{equation} \frac{1}{40} \end{equation}\) (b) \(\begin{equation} \frac{1}{80} \end{equation}\) (c) \(\begin{equation} \frac{1}{20} \end{equation}\) (d) \(\begin{equation} \frac{1}{60} \end{equation}\) (a) -
Sunil goes to market for buying an aquarium for his house. He asked to the shopkeeper to put some fish in the aquarium. The shopkeeper takes out 13 guppy fish, 18 flowerhorn fish, 12 koi fish and 11 angel fish from the big tank he had and put them in the aquarium that Sunil had bought. Now, he selects a fish at random.

On the basis of above information, answer the following questions.
(i) If total number of male fish in the aquarium is 36, then the probability of selecting a female fish is(a) \(\begin{equation} \frac{1}{2} \end{equation}\) (b) \(\begin{equation} \frac{1}{3} \end{equation}\) (c) \(\begin{equation} \frac{1}{4} \end{equation}\) (d) \(\begin{equation} \frac{1}{5} \end{equation}\) (ii) The probability of selecting a flowerhorn fish is
(a) \(\begin{equation} \frac{1}{2} \end{equation}\) (b) \(\begin{equation} \frac{1}{3} \end{equation}\) (c) \(\begin{equation} \frac{1}{4} \end{equation}\) (d) \(\begin{equation} \frac{1}{5} \end{equation}\) (iii) The probability of not selecting a koi fish is
(a) \(\begin{equation} \frac{2}{9} \end{equation}\) (b) \(\begin{equation} \frac{1}{3} \end{equation}\) (c) \(\begin{equation} \frac{1}{4} \end{equation}\) (d) \(\begin{equation} \frac{7}{9} \end{equation}\) (iv) The probability of selecting neither angle fish nor flowerhorn fish is
(a) \(\begin{equation} \frac{16}{27} \end{equation}\) (b) \(\begin{equation} \frac{25}{54} \end{equation}\) (c) \(\begin{equation} \frac{8}{27} \end{equation}\) (d) \(\begin{equation} \frac{25}{27} \end{equation}\) (v) The probability of selecting a guppy fish is
(a) 0 (b) 1 (c) \(\begin{equation} \frac{13}{54} \end{equation}\) (d) None of these (a) -
Two friends were playing a game with two dice. Anju has a blue dice and Nitish has a grey dice. They decided to throw both the dice simultaneously and note down all the possible outcomes appearing on the top of both the dice.

On the basis of above information, answer the following questions.
(i) The total number of possible outcomes they noted, is(a) 24 (b) 36 (c) 18 (d) 6 (ii) The probability of getting the sum of numbers on two dice is 16, is
(a) 1 (b) \(\begin{equation} \frac{5}{36} \end{equation}\) (c) 0 (d) \(\begin{equation} \frac{18}{35} \end{equation}\) (iii) The probability that both the numbers are prime numbers, is
(a) 0 (b) \(\begin{equation} \frac{1}{2} \end{equation}\) (c) \(\begin{equation} \frac{1}{4} \end{equation}\) (d) \(\begin{equation} \frac{1}{8} \end{equation}\) (iv) The probability that product of two numbers is odd, is|
(a) 1 (b) \(\begin{equation} \frac{1}{2} \end{equation}\) (c) \(\begin{equation} \frac{1}{4} \end{equation}\) (d) \(\begin{equation} \frac{1}{8} \end{equation}\) (v) The probability that difference between numbers is zero, is
(a) \(\begin{equation} \frac{1}{2} \end{equation}\) (b) \(\begin{equation} \frac{1}{4} \end{equation}\) (c) \(\begin{equation} \frac{1}{6} \end{equation}\) (d) \(\begin{equation} \frac{1}{8} \end{equation}\) (a) -
Four friends are playing with cards. One of them hides all the 2's, 5's and Jacks from the deck of 52 cards and then shuffles the remaining cards. Now, he tells to one of his friend to pick a card at random from the remaining cards.

On the basis of above information, answer the following questions.
(i) The probability of getting '6 of spade' is(a) 0 (b) \(\begin{equation} \frac{1}{20} \end{equation}\) (c) \(\begin{equation} \frac{1}{40} \end{equation}\) (d) 1 (ii) The probability of getting a black diamond is
(a) 0 (b) 1 (c) \(\begin{equation} \frac{1}{2} \end{equation}\) (d) \(\begin{equation} \frac{1}{4} \end{equation}\) (iii) The probability of getting a face card is
(a) \(\begin{equation} \frac{1}{3} \end{equation}\) (b) \(\begin{equation} \frac{1}{5} \end{equation}\) (c) \(\begin{equation} \frac{1}{7} \end{equation}\) (d) \(\begin{equation} \frac{1}{9} \end{equation}\) (iv) The probability of getting a club is
(a) 0 (b) 1 (c) \(\begin{equation} \frac{1}{2} \end{equation}\) (d) \(\begin{equation} \frac{1}{4} \end{equation}\) (v) The probability of getting a red card is
(a) 0 (b) 1 (c) \(\begin{equation} \frac{1}{2} \end{equation}\) (d) \(\begin{equation} \frac{1}{4} \end{equation}\)
(a) -
In a toy shop, there is a spinning wheel for their customers. The spinning wheel has different types of prizes as shown in figure. A customer can only spin the wheel after buying something from the shop.
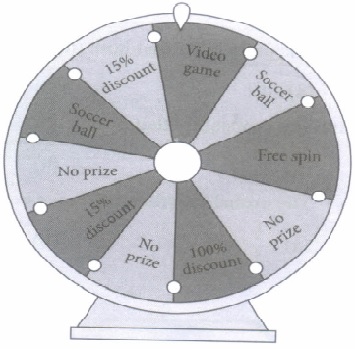
On the basis of above information, answer the following questions.
(i) If Mr Sharma spins the wheel, then the probability that he gets 100% discount is(a) 0 (b) \(\begin{equation} \frac{1}{10} \end{equation}\) (c) \(\begin{equation} \frac{1}{5} \end{equation}\) (d) \(\begin{equation} \frac{1}{4} \end{equation}\) (ii) If Anita spins the wheel, then the probability of getting no prize is
(a) \(\begin{equation} \frac{1}{10} \end{equation}\) (b) \(\begin{equation} \frac{1}{5} \end{equation}\) (c) \(\begin{equation} \frac{3}{10} \end{equation}\) (d) \(\begin{equation} \frac{2}{5} \end{equation}\)
(iii) Anshu spins the wheel, the probability that the wheel stops at soccer ball is(a) \(\begin{equation} \frac{1}{10} \end{equation}\) (b) \(\begin{equation} \frac{1}{5} \end{equation}\) (c) \(\begin{equation} \frac{3}{10} \end{equation}\) (d) \(\begin{equation} \frac{2}{5} \end{equation}\) (iv) The probability that one customer wins 15% discount is
(a) \(\begin{equation} \frac{1}{10} \end{equation}\) (b) \(\begin{equation} \frac{1}{5} \end{equation}\) (c) \(\begin{equation} \frac{3}{10} \end{equation}\) (d) \(\begin{equation} \frac{2}{5} \end{equation}\) (v) The probability of getting a free spin is
(a) \(\begin{equation} \frac{1}{10} \end{equation}\) (b) \(\begin{equation} \frac{1}{5} \end{equation}\) (c) \(\begin{equation} \frac{3}{10} \end{equation}\) (d) \(\begin{equation} \frac{2}{5} \end{equation}\) (a) -
Mr Verma is a production manager in a factory that makes footballs. On one day, he noticed that at every 100
pieces produced in the factory, 15 are defective. If the total number of footballs produced in one day in the
factory is 22000, then answer the following questions.

(i) A football is selected at random, then the probability of selecting a defective football is(a) \(\begin{equation} \frac{1}{20} \end{equation}\) (b) \(\begin{equation} \frac{1}{10} \end{equation}\) (c) \(\begin{equation} \frac{3}{20} \end{equation}\) (d) \(\begin{equation} \frac{1}{5} \end{equation}\) (ii) A football is selected at random, the probability of selecting a non-defective football is
(a) \(\begin{equation} \frac{1}{20} \end{equation}\) (b) \(\begin{equation} \frac{13}{20} \end{equation}\) (c) \(\begin{equation} \frac{3}{4} \end{equation}\) (d) \(\begin{equation} \frac{17}{20} \end{equation}\) (iii) The total number of defective footballs produced in one day is
(a) 4200 (b) 3300 (c) 9200 (d) 11000 (iv) The total number of non-defective footballs produced in one day is
(a) 18700 (b) 17800 (c) 12800 (d) 11000 (v) If the probability of selecting a defective football is , then the number of non-defective footballs produced in one day, if everyday same number of footballs produced in the factory, is
(a) 13640 (b) 9200 (c) 7040 (d) 14960 (a) -
Two families- Gupta's and Singhal's are lived in a colony. Gupta family has two children while Singhal family has 3 children.

On the basis of the above information, answer the following questions.
(i) Find the probability that Mr Singhal has exactly 2 girls and 1 boy.(a) \(\begin{equation} \frac{1}{2} \end{equation}\) (b) \(\begin{equation} \frac{1}{4} \end{equation}\) (c) \(\begin{equation} \frac{1}{6} \end{equation}\) (d) \(\begin{equation} \frac{1}{8} \end{equation}\) (ii) The probability that Gupta's has atleast 1 boy is
(a) \(\begin{equation} \frac{1}{3} \end{equation}\) (b) \(\begin{equation} \frac{2}{3} \end{equation}\) (c) 1 (d) \(\begin{equation} \frac{4}{5} \end{equation}\) (iii) The probability that Gupta's has atmost 1 girl is
(a) \(\begin{equation} \frac{1}{3} \end{equation}\) (b) \(\begin{equation} \frac{2}{3} \end{equation}\) (c) 1 (d) \(\begin{equation} \frac{2}{5} \end{equation}\) (iv) The probability that Singhal's has no boy is
(a) \(\begin{equation} \frac{1}{2} \end{equation}\) (b) \(\begin{equation} \frac{1}{4} \end{equation}\) (c)\(\begin{equation} \frac{1}{6} \end{equation}\) (d) \(\begin{equation} \frac{1}{8} \end{equation}\) (v) The sum of probabilities that both families have exactly two girls is
(a) \(\begin{equation} \frac{1}{12} \end{equation}\) (b) \(\begin{equation} \frac{1}{4} \end{equation}\) (c) \(\begin{equation} \frac{7}{12} \end{equation}\) (d) 0 (a) -
Vishal goes to a store to purchase juice cartons for his shop. The store has 80 cartons of orange juice, 90 cartons of apple juice, 38 cartons of mango juice and 42 cartons of guava juice. If Vishal chooses a carton at random, then answer the following questions.

(i) The probability that the selected carton is of apple juice is(a) \(\begin{equation} \frac{.1}{25} \end{equation}\) (b) \(\begin{equation} \frac{8}{25} \end{equation}\) (c) \(\begin{equation} \frac{13}{25} \end{equation}\) (d) \(\begin{equation} \frac{9}{25} \end{equation}\) (ii) The probability that the selected carton is not of orange juice is
(a) \(\begin{equation} \frac{14}{25} \end{equation}\) (b) \(\begin{equation} \frac{11}{25} \end{equation}\) (c) \(\begin{equation} \frac{17}{25} \end{equation}\) (d) \(\begin{equation} \frac{4}{25} \end{equation}\) (iii) The probability of selecting a carton of guava juice is
(a) \(\begin{equation} \frac{51}{125} \end{equation}\) (b) \(\begin{equation} \frac{16}{125} \end{equation}\) (c) 0 (d) \(\begin{equation} \frac{21}{125} \end{equation}\) (iv) Vishal buys 4 cartons of apple juice, 3 cartons of orange juice and 3 cartons of guava juice. A customer comes to Vishal's shop and picks a tetrapack of juice at random. The probability that the customer picks a guava juice, if each carton has 10 tetrapacks of juice, is
(a) \(\begin{equation} \frac{1}{10} \end{equation}\) (b) \(\begin{equation} \frac{2}{10} \end{equation}\) (c) \(\begin{equation} \frac{3}{10} \end{equation}\) (d) \(\begin{equation} \frac{2}{5} \end{equation}\) (v) If the storekeeper bought 14 more cartons of apple juice, then the probability of selecting a tetrapack of apple juice from the store is
(a) \(\begin{equation} \frac{25}{127} \end{equation}\) (b) \(\begin{equation} \frac{50}{127} \end{equation}\) (c) \(\begin{equation} \frac{75}{127} \end{equation}\) (d) \(\begin{equation} \frac{100}{127} \end{equation}\) (a) -
In the month of May, the weather forecast department gives the prediction of weather for the month of June, The given table shows the probabilities of forecast of different days:
Days Sunny Cloudy Partially cloudy Rainy Probability \(\begin{equation} \frac{1}{2} \end{equation}\) x \(\begin{equation} \frac{1}{5} \end{equation}\) y 
If the forecast is 100% correct for June, then answer the following questions,
(i) The number of sunny days in June, is(a) 5 (b) 10 (c) 15 (d) 20 (ii) If the number of cloudy days in June is 5, then x =
(a) \(\begin{equation} \frac{1}{4} \end{equation}\) (b) \(\begin{equation} \frac{1}{6} \end{equation}\) (c) \(\begin{equation} \frac{1}{8} \end{equation}\) (d) \(\begin{equation} \frac{1}{10} \end{equation}\) (iii) The probability that the day is not rainy is
(a) \(\begin{equation} \frac{13}{15} \end{equation}\) (b) \(\begin{equation} \frac{11}{15} \end{equation}\) (c) \(\begin{equation} \frac{1}{15} \end{equation}\) (d) None of these (iv) If the sum of x < and y is \(\begin{equation} \frac{3}{10} \end{equation}\), then the number of rainy days in June is
(a) 1 (b) 2 (c) 3 (d) 4 (v) Find the number of partially cloudy days
(a) 2 (b) 4 (c) 6 (d) 8 (a)
Case Study
*****************************************
Answers
Probability Case Study Questions With Answer Key Answer Keys
-
Total number of coins = 50 + 48 + 36 + 28 + 8 = 170
(i) (c): Number of \(\begin{equation} ₹ \end{equation} \) 5 coins = 36
Required probability = \(\begin{equation} \frac{36}{70}=\frac{18}{85} \end{equation}\)
(ii) (b): Number of \(\begin{equation} ₹ \end{equation} \)20 coins = 8
Required probability = \(\begin{equation} \frac{8}{170}=\frac{4}{85} \end{equation}\)
(iii) (d): Number of \(\begin{equation} ₹ \end{equation} \)10 coins = 28
Probability (coin is of \(\begin{equation} ₹ \end{equation} \)10) = \(\begin{equation} \frac{28}{170} \end{equation}\)
Required probability = 1 - P(coin is of 10)
\(\begin{equation} =1-\frac{28}{170}=\frac{142}{170}=\frac{71}{85} \end{equation}\)
(iv) (a) : Total number of coins of \(\begin{equation} ₹ \end{equation} \)10 and \(\begin{equation} ₹ \end{equation} \) 20
= 28 + 8 = 36
Required probability = \(\begin{equation} \frac{36}{170}=\frac{18}{85} \end{equation}\)
(v) (a): Total number of coins of \(\begin{equation} ₹ \end{equation} \)1, \(\begin{equation} ₹ \end{equation} \)2 and \(\begin{equation} ₹ \end{equation} \) 5
= 50 + 48 + 36 = 134
Required probability = \(\begin{equation} \frac{134}{170}=\frac{67}{85} \end{equation}\) -
Total number of puppets in claw crane = 58 + 42 + 36 + 64 = 200
(i) (b): P(picking a tiger) = \(\begin{equation} \frac{36}{200}=\frac{9}{50} \end{equation}\)
(ii) (a): P(picking a monkey) = \(\begin{equation} \frac{64}{200}=\frac{8}{25} \end{equation}\)
(iii) (c) : P(picking a teddy bear) = \(\begin{equation} \frac{58}{200}=\frac{29}{100} \end{equation}\)
(iv) (d) : P(not picking a monkey) = 1 - P(picking a monkey)
\(\begin{equation} =1-\frac{8}{25}=\frac{17}{25} \end{equation}\)
(v) (d): P(picking a pokemon) = \(\begin{equation} \frac{42}{200}=\frac{21}{100} \end{equation}\)
P(not picking a pokemon) = 1 - P(picking a pokemon)
\(\begin{equation} =1-\frac{21}{100}=\frac{79}{100} \end{equation}\) -
Since, every student get one chocolate. So, number of chocolates Rohit has is equal to the number of students in the class.
(i) (a): Let number of milk chocolates Rohit has = x
Probability of distributing milk chocolates = \(\begin{equation} \frac{1}{3} \end{equation}\)
\(\begin{equation} \Rightarrow \frac{x}{54}=\frac{1}{3} \Rightarrow x=\frac{54}{3}=18 \end{equation}\)
(ii) (c): Let number of dark chocolates Rohit has = y
Probability of distributing dark chocolates = \(\begin{equation} \frac{4}{9} \end{equation}\)
\(\begin{equation} \Rightarrow \frac{y}{54}=\frac{4}{9} \Rightarrow y=\frac{4 \times 54}{9}=24 \end{equation}\)
(iii) (d) : Number of white chocolates Rohit has = 54 -(18 + 24) = 12
Required probability = \(\begin{equation} \frac{12}{54}=\frac{2}{9} \end{equation}\)
(iv) (b) : Total number of milk and white chocolates = 18 + 12 = 30
Required probability = \(\begin{equation} \frac{30}{54}=\frac{5}{9} \end{equation}\)
(v) (b): Since all students gets one chocolate. So, total number of chocolates distributed = 54
\(\begin{equation} \text { Required probability }=\frac{54}{54}=1 \end{equation}\) -
Total time = 3 mins = 3 x 60 sees = 180 secs
(i) (a): Required probability = \(\begin{equation} \frac{30}{180}=\frac{1}{6} \end{equation}\)
(ii) (a): Required probability = \(\begin{equation} \frac{45}{180}=\frac{1}{4} \end{equation}\)
(iii) (d) : P(music will stop within 2 mins) = \(\begin{equation} \frac{120}{180}=\frac{2}{3} \end{equation}\)
P(music will stop after 2 mins) = \(\begin{equation} 1-\frac{2}{3}=\frac{1}{3} \end{equation}\)
(iv) (b) : Required probability = 1 - P(music will stop within first 60 secs)
\(\begin{equation} =1-\frac{60}{180}=1-\frac{1}{3}=\frac{2}{3} \end{equation}\)
(v) (b): Required probability = \(\begin{equation} \frac{82}{180}=\frac{41}{90} \end{equation}\) -
Sample space (5) = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
\(\Rightarrow\)n(5) = 8
(i) (c): Let A be the event of getting atmost one tail.
A = {HHH, HHT, HTH, THH}
\(\Rightarrow\)n(A) = 4
Required probability = \(\begin{equation} \frac{4}{8}=\frac{1}{2} \end{equation}\)
(ii) (d): Let B be the event of getting exactly 1 head. B = {HTT, THT, TTH}
\(\Rightarrow\) n(B) = 3
Required probability = \(\begin{equation} \frac{3}{8} \end{equation}\)
(iii) (d) : Let C be the event of getting exactly 3 tails.
C = {TTT} \(\Rightarrow\) n( C) = 1
Required probability = \(\begin{equation} \frac{1}{8} \end{equation}\)\(\begin{equation} \frac{1}{8} \end{equation}\)\(\begin{equation} \frac{1}{8} \end{equation}\)\(\begin{equation} \frac{1}{8} \end{equation}\)
(iv) (b) : Let D be the event of getting atmost 3 heads.
D = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
\(\Rightarrow\)n(D) = 8
Required probability = \(\begin{equation} \frac{8}{8}=1 \end{equation}\)
(v) (c): Let E be the event of getting atleast two heads.
E = {HHT, HTH, THH, HHH}
\(\Rightarrow\)n(E) = 4
Required probability = \(\begin{equation} \frac{n(E)}{n(S)}=\frac{4}{8}=\frac{1}{2} \end{equation}\) -
Total number of blocks in the kit = 120
Number of red blocks = 40
Number of blue blocks = 25
Number of green blocks = 30
Number of yellow blocks = 120 - (40 + 25 + 30)
= 120 - 95 = 25
(i) (d): P(block is red) \(\begin{equation} =\frac{40}{120}=\frac{1}{3} \end{equation}\)
(ii) (c): P(block is not yellow) = 1 - P(block is yellow)
\(\begin{equation} =1-\frac{25}{120}=1-\frac{5}{24}=\frac{19}{24} \end{equation}\)
(iii) (c) : P(block is green) = \(\begin{equation} \frac{30}{120}=\frac{1}{4} \end{equation}\)
(iv) (b) : P(block is yellow) = \(\begin{equation} \frac{5}{24} \end{equation}\)
(v) (b): P(block is not blue) = 1 - P(block is blue)
\(\begin{equation} =1-\frac{25}{120}=1-\frac{5}{24}=\frac{19}{24} \end{equation}\) -
Total number of possible outcome, n(S) = 200
(i) (c): Let A be the event that number on selected card is divisible by 10.
A = {10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120,130, 140, 150,160, 170, 180, 190,200}
\(\Rightarrow\) n(A) = 20
\(\begin{equation} P(A)=\frac{n(A)}{n(S)}=\frac{20}{200}=\frac{1}{10} \end{equation}\)
(ii) (c) : Let B be the event that the number on the selected card is a prime number more than 100 but less than 150.
B = {101, 103, 107, 109, 113, 127, 131, 137, 139, 149}
\(\Rightarrow\)n(B) = 10
\(\begin{equation} P(B)=\frac{n(B)}{n(S)}=\frac{10}{200}=\frac{1}{20} \end{equation}\)
(iii) (c) : Let C be the event that the number on the selected card is a multiple number of 3.
C = {3, 6, 9,12, ..... ,192,195, 198}
\(\Rightarrow\) n(C) = 66
\(\begin{equation} P(C)=\frac{n(C)}{n(S)}=\frac{66}{200}=\frac{33}{100} \end{equation}\)
(iv) (a) : Let D be the event that the number on the selected card is a perfect square.
D = {I, 4, 9, 16,25,36,49,64,81, 100, 121, 144, 169, 196}
\(\Rightarrow\)n(D) = 14
\(\begin{equation} P(D)=\frac{n(D)}{n(S)}=\frac{14}{200}=\frac{7}{100} \end{equation}\)
(v) (a): Let E be the event that the number on the selected card is a perfect cube.
E = {I, 8, 27, 64, 125}
\(\Rightarrow\)n(E) = 5
\(\begin{equation} P(E)=\frac{5}{200}=\frac{1}{40} \end{equation}\) -
Total number of fish in the aquarium = 13 + 18 + 12 + 11 = 54
(i) (b): Number of male fish in the aquarium = 36
Number of female fish in the aquarium = 54 - 36 = 18
So, required probability = \(\begin{equation} \frac{18}{54}=\frac{1}{3} \end{equation}\)
(ii) (b): Required probability = \(\begin{equation} \frac{18}{54}=\frac{1}{3} \end{equation}\)
(iii) (d) : P(selecting a koi fish) = \(\begin{equation} \frac{12}{54}=\frac{2}{9} \end{equation}\)
P(not selecting a koi fish) = 1 - P(selecting a koi fish) \(\begin{equation} =1-\frac{2}{9}=\frac{7}{9} \end{equation}\)
(iv) (b) : Total number of guppy fish and koi fish = 13 + 12 = 25
P(selecting neither angel fish nor flowerhorn fish =25/54.
(v) (c): P(selecting a guppy fish) = 13/54. -
(i) (b):Total number of possible outcomes on throwing two dice simultaneously = 6 x 6 = 36
(ii) (c): As we know, that maximum sum of numbers on two dice = 6 + 6 = 12
It is an impossible event.
So, required probability = 0
(iii) (c) : Let A be the event that both the numbers on dice are prime.
A = {(2, 2), (2, 3), (2, 5), (3,2), (3, 3), (3, 5), (5, 2), (5,3), (5, 5)}
\(\Rightarrow\)n(A) = 9
\(\begin{equation} P(A)=\frac{9}{36}=\frac{1}{4} \end{equation}\)
(iv) (c) : Let B the event that product of two numbers is odd.
B = {(1, 1), (1, 3), (1, 5), (3,1), (3, 3), (3, 5), (5,1), (5,3), (5, 5)}
\(\Rightarrow\)n(B) = 9
\(\begin{equation} P(B)=\frac{9}{36}=\frac{1}{4} \end{equation}\)
(v) (c) : Let C be the event that difference of two numbers is zero.
C = {(1, 1), (2,2), (3, 3), (4,4), (5, 5), (6, 6)}
\(\Rightarrow\)n(C) = 6
\(\begin{equation} P(C)=\frac{6}{36}=\frac{1}{6} \end{equation}\) -
Total number of cards left = 52 - (4 + 4 + 4) = 52 - 12 = 40
There are four 2's, four 5's and four Jacks in a deck
(i) (c): P(getting 6 of spade) = \(\begin{equation} \frac{1}{40} \end{equation}\)
(ii) (a): As there is no black diamond in the deck of cards.
P(black diamond) = 0
(iii) (b) : Total number of face cards in a deck = 12
But all Jacks are removed
Number offace cards left = 12 - 4 = 8
So, P(getting a face card) = \(\begin{equation} \frac{8}{40}=\frac{1}{5} \end{equation}\)
(iv) (d) : Number of cards of club left = 13 - 3 = 10
3 cards are removed of each kind
P(getting a club) = \(\begin{equation} \frac{10}{40}=\frac{1}{4} \end{equation}\)
(v) (c): Number of red cards left = 26 - 6 = 20
P(getting a red card) = \(\begin{equation} \frac{20}{40}=\frac{1}{2} \end{equation}\) -
Total number of possible outcomes = 10
(i) (b): P(getting 100% discount) = \(\begin{equation} \frac{1}{10} \end{equation}\)
(ii) (c): P(getting no prize) = \(\begin{equation} \frac{3}{10} \end{equation}\)
(iii) (b) : P(getting a soccer ball) = \(\begin{equation} \frac{2}{10}=\frac{1}{5} \end{equation}\)
(iv) (b) : P(getting 15% discount) = \(\begin{equation} \frac{2}{10}=\frac{1}{5} \end{equation}\)
(v) (a): P(getting a free spin) = \(\begin{equation} \frac{1}{10} \end{equation}\) -
Total number of footballs produced in one day = 220000
(i) (c): P(selecting a defective football) = \(\begin{equation} \frac{15}{100}=\frac{3}{20} \end{equation}\)
(ii) (d): P(selecting a non-defective football) = 1- P(selecting a defective football) = \(\begin{equation} 1-\frac{3}{20}=\frac{17}{20} \end{equation}\)
(iii) (b) : Total number of defective footballs produced in 1 day = \(\begin{equation} \frac{3}{20} \times 22000=3300 \end{equation}\)
(iv) (a) : Total number of non-defective footballs produced in 1 day = 22000 - 3300 = 18700
(v) (d): P(selecting defective football) \(\begin{equation} =\frac{8}{25} \end{equation}\)
P (selecting non-defective football) = \(\begin{equation} 1-\frac{8}{25}=\frac{17}{25} \end{equation}\)
Number of non-defective footballs produced \(\begin{equation} =\frac{17}{25} \times 22000=14960 \end{equation}\) -
Let Band G denotes boy and girl respectively.
Then,
Possible outcomes for Gupta's family having two kids is {BB, BG, GG}
Similarly, possible outcomes for Singhal's family having 3 kids is {BBB, BBG, BGG, GGG}
(i) (b): Required probability = \(\begin{equation} \frac{1}{4} \end{equation}\)
(ii) (b): Required probability = \(\begin{equation} \frac{2}{3} \end{equation}\)
(iii) (b): Required probability = \(\begin{equation} \frac{2}{3} \end{equation}\)
(iv) (b) : Required probability = \(\begin{equation} \frac{1}{4} \end{equation}\)
(v) (c): Required probability = \(\begin{equation} \frac{1}{3}+\frac{1}{4}=\frac{7}{12} \end{equation}\) -
Total number of cartons in the store = 80 + 90 + 38 + 42 = 250
(i) (d) :P(choosing an apple juice carton) = \(\begin{equation} \frac{90}{250}=\frac{9}{25} \end{equation}\)
(ii) (c) : P( choosing an orange juice carton ) = \(\begin{equation} \frac{80}{250}=\frac{8}{25} \end{equation}\)
P(choosing not an orange juice carton) = \(\begin{equation} =1-\frac{8}{25}=\frac{17}{25} \end{equation}\)
(Iii) (d):P(choosing a guava juice carton) = \(\begin{equation} \frac{42}{250}=\frac{21}{125} \end{equation}\)
(iv) (c) : Total number of cartons Vishal bought =4+3+3=10
Number of tetrapacks in 1 carton = 10
Total number of tetrapacks Vishal has = 100
So, P( customer picks a guava juice tetrapack) \(\begin{equation} =\frac{3 \times 10}{100}=\frac{3}{10} \end{equation}\)
(v) (b): Number of cartons left with storekeeper = 250 - 10 = 240
Number of cartons he bought = 14
Total number of cartons are with storekeeper now = 240 + 14 = 254
So, P(selecting a tetrapack of apple juice from store) \(\begin{equation} =\frac{(90-4+14) \times 10}{254 \times 10}=\frac{100}{254}=\frac{50}{127} \end{equation}\) -
Total number of days in June = 30
(i) (c): Number of sunny days = PCsunny day) x 30 = \(\begin{equation} \frac{1}{2} \times 30=15 \end{equation}\)
(ii) (b): Number of cloudy days in June = 5
\(\begin{equation} x=\frac{5}{30}=\frac{1}{6} \end{equation}\)
(iii) (a): Required probability = \(\begin{equation} \frac{1}{2}+\frac{1}{6}+\frac{1}{5}=\frac{13}{15} \end{equation}\)
(iv) (d) : We have, \(\begin{equation} x+y=\frac{3}{10} \Rightarrow y=\frac{3}{10}-\frac{1}{6}=\frac{2}{15} \end{equation}\)
So, number of rainy days = \(\begin{equation} \frac{2}{15} \times 30=4 \end{equation}\)
(v) (c): Number of partially cloudy days = P(partially cloudy days) x 30 \(\begin{equation} =\frac{1}{5} \times 30=6 \end{equation}\)

























