Class 11th Applied Mathematics - Numbers, Quantification and Numerical Applications Case Study Questions and Answers 2022 - 2023
By QB365 on 09 Sep, 2022
QB365 provides a detailed and simple solution for every Possible Case Study Questions in Class 11 Applied Mathematics Subject - Numbers, Quantification and Numerical Applications, CBSE. It will help Students to get more practice questions, Students can Practice these question papers in addition to score best marks.
QB365 - Question Bank Software
Numbers, Quantification and Numerical Applications Case Study Questions With Answer Key
11th Standard CBSE
-
Reg.No. :
Applied Mathematics
-
Four students of class XI, discussing about the binary number system, During their discussion they prepared the following notes and table on binary numbers.

The binary number system, also referred to as base 2 system, makes use of only two digits i.e.,1 and 0. ' Bi ' in binary is analogous to bi in bicycle (two wheels). Each digit of the binary system called a bit originating from binary digit. Some examples of binary numbers are 1001011, 1011.101, 1111.01 etc. A binary number can be mapped to an equivalent decimal number that can be easily understood by human.Decimal Binary 0 0 1 1 2 10 3 11 4 100 5 101 6 110 7 111 8 1000 9 1001 On the basis of the above information answer the following questions:
(i) The value of base in binary system is(a) 1 (b) 10 (c) 3 (d) 2 (ii) Which of the following is not a binary number?
(a) 111 (b) 101 (c) 101E (d) 1001 (iii) Which of the following is the correct representation of binary number?
(a) (125)2 (b) (101)2 (c) 110 (d) (101)2 (iv) If the decimal number is a fraction then its binary equivalent is obtained by ____________ the number continuously by 2.
(a) dividing (b) adding (c) subtracting (d) multiplying (v) The binary equivalent of the decimal number 10 is
(a) 0010 (b) 0101 (c) 1010 (d) 1001 (a) -
In class of XI, teacher was describing logarithm to students. In logarithm, he states two properties which are as mentioned below:
On the basis of this information answer the following questions:
(i) log (a+b) = log a+ log b, is this statement true or false ?(a) False (b) True (c) Can’t say (d) None of these (ii) The value of log 5 + log 2 is equal to
(a) 1 (b) log 7 (c) log 8 (d) log \(\frac{5}{2}\) (iii)The value of log \(\frac{10}{2}+\log \frac{22}{11} \text { is }\)
(a) 0 (b) 1 (c) log 7 (d) log 5 (iv) log \(\frac{32}{4}\) is equal to
(a) log 32 – log 4 (b) log 16 – log 2 (c) log 9 (d) log 6 (v) \(\log \frac{25}{27}+\log \frac{81}{125}+\log \frac{25}{3} \text { is }\)equal to
(a) log (b) log 2 (c) 0 (d) log 5 (a) -
A teacher of class XI, taking class on number system. In number system he was trying to explain the addition and subtraction of binary number. He tried to give explanation as per the following details:

(i) Additional of Binary Numbers
The binary number system used only two digits 0 and 1 due to which their addition is simple. There are four basic operations for binary addition as mentioned below.
(i) 0 + 0 = 0
(ii) 0 + 1 = 1,
(iii) 1 + 0 = 1
(iv) 1 + 1 = 10 (with carry 1)
For example: Consider two binary number 11101 and 11011, then

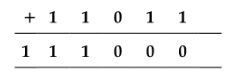
The above sum is carried out by following steps:
For 1 + 1 = 10 = 0 with carry of 1
For 1 + 0 + 1 = 10 = 0 with carry of 1
For 1 + 1 + 0 = 10 = 0 with carry of 1
For 1 + 1 + 1 = 10 + 1 = 11 with carry of 1
For 1 + 1 + 1 = 11
Thus,11101 + 11011 = 111000
Note: 10 + 1 = 11, which is equivalent to two + one = three (the next binary number after 10.)
(ii) Subtraction of Binary Numbers
The subtraction of the binary digit depends on the four basic operations given as follows:
(i) 0 – 0 = 0
(ii) 1 – 0 = 1
(iii) 1 – 1 = 0
(iv) 10 – 1 = 1 (0 – 1 = 1 by borrowing 1)
The above first three operations are easy to understand as they are identical to decimal subtraction, the fourth operation can be understand with the logic two minus one is one (i.e, 2 –1 = 1).
For example: Consider to binary numbers 1100 and 1010, then
\(\begin{array}{rlll} & 0 & 10 & \leftarrow \text { borrow } \\ 1 & 1 & 0 & 0 \\ -1 & 0 & 1 & 0 & \\ \hline 0 & 0 & 1 & 0 & \\ \hline \end{array}\)
The above subtraction is carried out through following steps:
For 0 – 0 = 0
For 0 – 1 = 1, taking borrow 1 and then 10 – 1 = 1
For 1 – 0, since 1 has already been given, it becomes 0 – 0 = 0
For 1 – 1 = 0
Thus, 1100 – 1010 = 0010
Answer the following questions on the basis of this information.
(i) What is the sum of binary numbers 111 + 100?(a) 1001 (b) 1010 (c) 1011 (d) 1010 (ii) What is difference of two binary numbers 1011 –101 ?
(a) 0110 (b) 0111 (c) 1110 (d) 0100 (iii) What is the value of 11011 + 10101?
(a) 110011 (b) 111000 (c) 110010 (d) 110000 (iv) What is the value of 1101101–11011 ?
(a) 1010010 (b) 1110010 (c) 1011110 (d) 1001110 (v) Find decimal equivalent of Binary Number(1011.011)2?
(a) (9.375)10 (b) (10.375)10 (c) (11.375)10 (d) (11.2)10 (a) -
A group of students were discussing logarithm properties as there exams were approaching. They prepared notes on base changing properties on logarithm for quick revision before examination.
On the basis of this information answer the following questions:
(i) The value of log 2 8 is equal to(a) 0 (b) 1 (c) log 2 (d) 3 (ii) The value of log23169 is equal
(a) 10 (b) 4 (c) 8 (d) 1 (iii) \(\frac{\log 27 \times \log 16 \times \log 125}{4}=\alpha \text {, then the value of } \alpha \text { is }\)
(a) 25 (b) 3 (c) log 2 (d) 16 (iv) If logabc = x, logbca = y, logcab = z, \(\text { then } \frac{1}{x+1}+\frac{1}{y+1}=\frac{1}{z+1}=\)
(a) 0 (b) 5 (c) 2 (d) 1 (v) If 2 log a = 4 log 3, then find the value of
(a) 8 (b) 9 (c) 5 (d) 6 (a) -
I In cricket matches, scores of all the players are recorded to find the average of their batting and bowling. Data of few batsmen are recorded as mentioned below:
Name of Player Score in 1st Match
Score in 2nd Match Score in 3rd Match Score in 4th Match Score in 5th Match Sachin Tendulka 95 87 59 67 88 Rahul Dravid 88 79 76 74 86 Virendra Sehwag 97 56 63 44 89 On the basis of this information teacher ask students various questions as mentioned below:
(i) What is the average score of Sachin Tendulkar?(a) 78.2 b) 79.2 (c) 83.2 (d) 81 (ii) What is the average score of Rahul Dravid ?
(a) 81.2 (b) 80.6 (c) 85.2 (d) 80.2 (iii) What is the average score of Virendra Sehwag ?
(a) 71.2 (b) 73.5 (c) 74.5 (d) 69.8 (iv) What is the approximate average of sum of average scores of Sachin Tendulkar and Rahul Dravid?
(a) 83 (b) 84 (c) 80 (d) 7 (v) If the second and third score of Virendra Sehwag is replaced from 56 to 95 and 63 to 89 what will be the new average score ?
(a) 84 (b) 82.8 (c) 81.5 (d) 83 (a) -
Few students with their teacher went to an education trip. They saw few persons were working in a field. The teacher discussed few concepts related to time and work, which are as follows:
Rule 1: If M1 persons can do W1 work in D1 days and M2 persons can do W2 work in D2 days, then we can say:
M1 × D1 × W1 = M2 × D2 × W2
1. If the persons work T1 andT2 hours per day, respective, then the equation gets modified to M1 × D1 × W1 × T1 = M2 × D2 × W2 × T2
2. It the person's efficiency are E1 and E2, respectively, then M1 × D1 × W1 × T1 × E1= M2 × D2 × W2 × T2 × E2
Rule 2: If A can do a piece of work in n days, then the work done by A in one day = \(\frac{1}{n}\) th part of whole work.
Rule 3: If A's one day's work = \(\frac{1}{n}\)th part of whole work, then A can finish the work in n days.
Rule 4: If A can do a work in D1 days and B can do the same work in D2 days, then A and B together can do the same work in \(\frac{D_{1} \cdot D_{2}}{L \ D_{1}+D_{2} I}days.\)
On the basis of this information teacher ask students various questions as mentioned below:
(i) If 15 men working 9 hours a day, can reap a field in 16 days, in how many days will 18 men reap the field, working 8 hours a day.(a) 11 (b) 12 (c) 15 (d) 10 (ii) 'A' can do a piece of work in 5 days and 'B' can do it in 6 days. How long will they take if both work together ?
(a) \(4 \frac{8}{11}\) (b) \(2 \frac{3}{11}\) (c) \(2 \frac{8}{11}\) (d) \(3 \frac{8}{13}\) (iii) A man can do a piece of work in 5 days, but with the help of his son, he can do it in 3 days. In what time can the son do it alone ?
(a) \(6 \frac{1}{5}\) (b) \(9 \frac{1}{5}\) (c) \(7 \frac{1}{2}\) (d) \(3 \frac{1}{5}\) (iv) 'A' does a work in 10 days and ’B’ does the same work in 15 days. In how many days they together will do the same work ?
(a) 2 (b) 3 (c) 5 (d) (v) ’A’ can finish a work in 18 days and ’B’ can do the same work in half the time taken by ’A’ then, working together, what part of the same work they can finish in a day.
(a) \(\frac{1}{4}\) (b) \(\frac{1}{6}\) (c) \(\frac{1}{5}\) (d) \(\frac{1}{3}\) (a)
Case Study
*****************************************
Answers
Numbers, Quantification and Numerical Applications Case Study Questions With Answer Key Answer Keys
-
(i) (d): 2
The base in binary system is 2.
(ii) (c): 101E
A binary number can have only two possible digits 0 and 1.
(iii) (d): (101)2
The binary numbers should comprise only two digits 0 and 1. Also, for the base, the value should be 2 and it should be written as a subscript enclosing the entire number.
(iv) (d): multiplying
On multiplying the decimal continuously by 2, the binary equivalent is obtained by the collection of the integer parts.
(v) (c): 1010
To get the binary equivalent of any number, we need to divide the number by 2 and obtain remainder as:
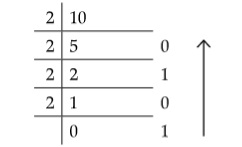
Now, we write the remainder in the reverse order as 1010. -
(i) (a): False
According to Law 1 log a ( mn ) = log a m + log an. So, log( a + b) ≠ log a + log
(ii) (a): 1
log 5 + log 2 = log 10 = 1
(iii) (b): 1
\(\log \frac{10}{2}+\log \frac{22}{11}=\log 5+\log 2\)
= log 10
= 1
(iv) (a): log 32 – log 4
Using property log \(\frac{a}{b}=\log a-\log b\)
(v) (d): log 5
\(\log \frac{25}{27}+\log \frac{81}{125}+\log \frac{25}{3}=\log \left(\frac{25}{27} \times \frac{81}{125} \times \frac{25}{3}\right)\)
= log 5 -
(i) (c): 1011
1011, because
\(\begin{array}{r} 1 \quad 1 & 1 \\ +\quad 10 & 0 \\ \hline 10 \quad 1 & 1 \\ \hline \end{array}\)
(ii) (a): 0110
0110, because
\(\begin{array}{rlll} 1 & 0 & 1 & 1 \\ - & 1 & 0 & 1 \\ \hline 0 & 1 & 1 & 0 \\ \hline \end{array}\)
(iii) (d): 110000
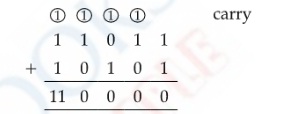
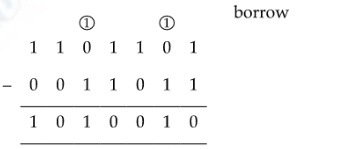
(iv) (a): 1010010
(v) (c): (11.375)10
Binary to Decimal conversion is btained by multiplying 2 to the power of base index along with the value at that index position.
\(\begin{array}{lcccccccc} \text { Digit } & 1 & 0 & 1 & 1 & . & 0 & 1 & 1 \\ \text { Fractional value } & 2^{3} & 2^{2} & 2^{1} & 2^{0} & . & 2^{-1} & 2^{-2} & 2^{-3} \end{array}\)
\(\text { Decima valuel } 1 \times 2^{3} 0 \times 2^{2} 1 \times 2^{1} 1 \times 2^{0} .0 \times 2^{-1} 1 \times 2^{-2} 1 \times 2^{-3}\)
= 8 + 0 + 2 + 1 . 0 + 0.25 + 0.125
= 11.375
Hence, (1011.011)2 = (11.375)10 -
(i) (d): 3
log28 = 3 log2 2 = 3
(ii) (d): 12
\(\log _{2} 316^{9}=\frac{9}{2} \log _{2} 16\)
= 3 log224
= 12 log22
= 12
(iii) (b): 36
\(\frac{\log 27 \times \log 16 \times \log 125}{\log 3 \times \log 2 \times \log 5}=\frac{3 \log 3 \times 4 \log 2 \times 3 \log 5}{\log 3 \times \log 2 \times \log 5}\)
= 36
(iv) (d): 1
x + 1 = logabc + loga a = logaabc
y+ 1 = logbca+ logbb= logbabc
z+ 1 = logcab+ logcc= logcabc
Therefore, \(\frac{1}{x+1}+\frac{1}{y+1}+\frac{1}{z+1}=\frac{1}{\log _{a} a b c}+\frac{1}{\log _{b} a b c}+\frac{1}{\log _{c} a b c}\) \(\begin{aligned} &=\log _{a b c} a+\log _{a b c} b+\log _{a b c} c \end{aligned}\)
\(\begin{aligned} &=\log _{\pi / v} a b c=1\end{aligned}\)
(v) (b): 9
2 loga= 4 log 3
⇒ loga2 = log34
⇒ 2 = (32)2
⇒ a = 32= 9 -
(i) (b): 79.2
Sum of all scores = 396 Average
= \(\frac{396}{5}\)
= 79.2
(ii) (b): 80.6
Sum of all scores = 403
Average = \(\frac{403}{3}\)
= 80.6
(iii) (d): 69.8
Sum of scores = 349
Average Score \(\frac{349}{5}\)
= 69.8
(iv) (c): 80
Sum = 80.6 + 79.2 = 159.8
Average = \(\frac{159.8}{2}\)
= 79.9 = 80 (approx.)
(v) (b): 82.8
New scores = 97 , 95 , 89, 44, 89
Total of scores = 414
Average Score = \(\frac{414}{5}\)
= 82.8 -
(i) (c): 15
Here, M1 = 15, D1 = 16, T1 = 9 hours, M2 = 18 and T2 = 8 hours
Using formula, M1 × D1 × T1 = M2 × D2 × T
D2 = \(\frac{M_{1} \times D_{1} \times T_{1}}{M_{2} \times T_{2}}\)
\(\Rightarrow \quad D_{2}=\frac{15 \times 16 \times 9}{18 \times 8}=15 \text { days }\)
Hence, required number of days are 15.
(ii) (c): \(2 \frac{8}{11}\)
Suppose, A can do a piece of work in D1 days and B can do the same work in D2 days.
Here, given D1 = 5 days and D2 = 6 days
Thus, A and B can do this work in \(\frac{D_{1} \times D_{2}}{D_{1}+D_{2}} \text { days }\)
i.e., \(\frac{5 \times 6}{5+6}=\frac{30}{11}=2 \frac{8}{11} \text { days. }\)
(iii) (c): \(7 \frac{1}{2}\)
Son's 1 day's work = \(\left(\frac{1}{3}-\frac{1}{5}\right)=\frac{2}{15}\)
༜ The son alone can do the work in \(\frac{15}{2}=7 \frac{1}{2} \text { days }\)
(iv) (d): 6
A's 1 day's work = \(\frac{1}{10}\)
B's 1 day's work = \(\frac{1}{15}\)
༜ ( A + B )'s 1 day's work = \(\frac{1}{10}+\frac{1}{15}=\frac{1}{6}\)So, A and B together can be the work in 6 days
(v) (b): \(\frac{1}{6}\)
\(\frac{1}{6} \text { th part, because }\)
\(A \text { 's } 1 \text { day's work }=\frac{1}{18}\)
\(B^{\prime} \text { s } 1 \text { day's work }=\frac{1}{9}\)
\(\therefore \ (A+B)^{\prime} \mathrm{s} 1 \text { work }=\left(\frac{1}{18}+\frac{1}{9}\right)=\frac{1}{6}\)
Hence, A and B together finish 16 th part of the work in a day.
Case Study



































