12th Standard CBSE Physics Model Question paper

Class 12th Physics - Alternating Current Case Study Questions and Answers 2022 - 2023

By QB365 on 09 Sep, 2022

QB365 provides a detailed and simple solution for every Possible Case Study Questions in Class 12th Physics Subject - Alternating Current, CBSE. It will help Students to get more practice questions, Students can Practice these question papers in addition to score best marks.

QB365 - Question Bank Software

Alternating Current Case Study Questions With Answer Key

12th Standard CBSE

Physics

Time : 01:15:00 Hrs

Total Marks : 55

Case Study

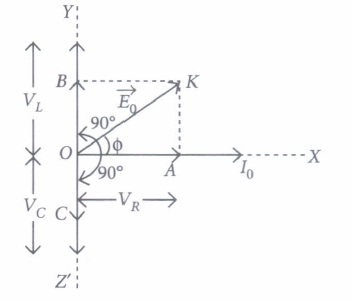
When a pure resistance R, pure inductor L and an ideal capacitor of capacitance C is connected in series to a source of alternating e.m.f., then current at any instant through the three elements has the same amplitude and is represented as I = I_osinwt. However, voltage across each element has a different phase relationship with the current as shown in graph.
The effective resistance of RLC circuit is called impedance (2) of the circuit and the voltage leads the current by a phase angle \(\phi .\)

A resistor of \(12 \Omega\) a capacitor of reactance \(14 \Omega\) and a pure inductor of inductance 0.1 H are joined in series and placed across 200 V, 50 Hz a.c. supply
(i) The value of inductive reactance is

\(\text { (a) } 15 \Omega\)

\(\text { (b) } 31.4 \Omega\)

\(\text { (c) } 20 \Omega\)

\(\text { (d) } 30 \Omega\)

(ii) The value of impedance is

\(\text { (a) } 20 \Omega\)

\(\text { (b) } 15 \Omega\)

\(\text { (c) } 30 \Omega\)

\(\text { (d) } 21.13 \Omega\)

(iii) What is the value of current in the circuit?

(a) 5 A

(b) 15 A

(c) 10 A

(d) 9.46 A

(iv) What is the value of the phase angle between current and voltage?

\(\text { (a) } 53^{\circ} 9^{\prime}\)

\(\text { (b) } 63^{\circ} 9^{\prime}\)

\(\text { (c) } 55^{\circ} 4^{\prime}\)

(d) 50°

(v) From graph, which one is true from following?

\(\text { (a) } V_{L} \geq V_{C}\)

\(\text { (b) } V_{L}<V_{C}\)

\(\text { (c) } V_{L}>V_{C}\)

\(\text { (d) } V_{L}=V_{C}\)

Let a source of alternating e.m.f. E = E_osinrot be connected to a capacitor of capacitance C. If 'I' is the instantaneous value of current in the circuit at instant t, then \(I=\frac{E_{0}}{1 / \omega C} \sin \left(\omega t+\frac{\pi}{2}\right)\) The capacitive reactance limits the amplitude of current in a purely capacitive circuit and it is given by \(X_{C}=\frac{1}{\omega C}\)

(i) What is the unit of capacitive reactance?

(a) farad

(b) ampere

(c) ohm

(d) ohm^-1

(ii) The capacitive reactance of a \(5 \mu \mathrm{F}\) lFcapacitor for a frequency of 10⁶Hz is

\(\text { (a) } 0.032 \Omega\)

\(\text { (b) } 2.52 \Omega\)

\(\text { (c) } 1.25 \Omega\)

\(\text { (d) } 4.51 \Omega\)

(iii) In a capacitive circuit, resistance to the flow of current is offered by

(a) resistor

(b) capacitor

(c) inductor

(d) frequency

(iv) In a capacitive circuit, by what value of phase angle does alternating current leads the e.m.f?

(a) 45°

(b) 90°

(c) 75°

(d) 60°

(v) One microfarad capacitor is joined to a 200 V, 50 Hz alternator. The rms current through capacitor is

\(\text { (a) } 6.28 \times 10^{-2} \mathrm{~A}\)

\(\text { (b) } 7.5 \times 10^{-4} \mathrm{~A}\)

\(\text { (c) } 10.52 \times 10^{-2} \mathrm{~A}\)

\(\text { (d) } 15.25 \times 10^{-2} \mathrm{~A}\)

Let a source of alternating e.m.f E = E_osinrot be connected to a circuit containing a pure inductance L. If I is the value of instantaneous current in the circuit, then \(I=I_{0} \sin \left(\omega t-\frac{\pi}{2}\right)\).The inductive reactance limits the current in a purely inductive circuit and is given by \(X_{L}=\omega L\)

(i) A 100 hertz a.c. is flowing in a 14 mH coil. The reactance is

\(\text { (a) } 15 \Omega\)

\(\text { (b) } 7.5 \Omega\)

\(\text { (c) } 8.8 \Omega\)

\(\text { (d) } 10 \Omega\)

(ii) In a pure inductive circuit, resistance to the flow of current is offered by

(a) resistor

(b) inductor

(c) capacitor

(d) resistor and inductor

(iii) In a inductive circuit, by what value of phase angle does alternating current lags behind e.m.f.?

45^o

90^o

(c) 120°

75^o

(iv) How much inductance should be connected to 200 V, 50 Hz a.c. supply so that a maximum current of 0.9 A flows through it?

(a) 5 H

(b) 1 H

(c) 10 H

(d) 4.5 H

(v) The maximum value of current when inductance of 2 H is connected to 150 volt, 50 Hz supply is

(a) 0.337 A

(b) 0.721 A

(c) 1.521 A

(d) 2.522 A

The power averaged over one full cycle of a.c. is known as average power. It is also known as true power
\(P_{\mathrm{av}}=V_{\mathrm{rms}} I_{\mathrm{rms}} \cos \phi=\frac{V_{0} I_{0}}{2} \cos \phi\)
Root mean square or simply rms watts refer to continuous power
A circuit containing a 80.mH inductor and a \(60 \mu \mathrm{F}\) capacitor in series is connected to a 230 V, 50 Hz supply. The resistance of the circuit is negligible.

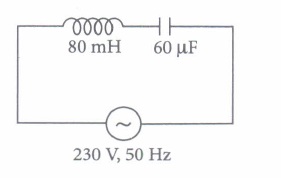
(i) The value of current amplitude is

(a) 15 A

(b) 11.63 A

(c) 17.65 A

(d) 6.33 A

(ii) Find rms value.

(a) 6 A

(b) 5.25 A

(c) 8.23 A

(d) 7.52A

(iii) The average power transferred to inductor is

(a) zero

(b) 7W

(c) 2.5 W

(d) 5 W

(iv) The average power transferred to the capacitor is

(a) 5 W

(b) zero

(c) 11 W

(d) 15 W

(v) What is the total average power absorbed by the circuit?

(a) zero

(b) 10W

(c) 2.5 W

(d) 15W

A transformer is essentially an a.c. device. It cannot work on d.c. It changes alternating voltages or currents. It does not affect the frequency of a.c. It is based on the phenomenon of mutual induction. A transformer essentially consists of two coils of insulated copper wire having different number of turns and wound on the same soft iron core.
The number of turns in the primary and secondary coils of an ideal transformer are 2000 and 50 respectively. The primary coil is connected to a main supply of 120 V and secondary coil is connected to a bulb of resistance \(0.6 \Omega\)
(i) The value of voltage across the secondary coil is

(a) 5V

(b) 2V

(c) 3 V

(d) 10 V

(ii) The value of current in the bulb is

(a) 7 A

(b) 15 A

(c) 3 A

(d) 5 A

(iii) The value of current in primary coil is

(a) 0.125 A

(b) 2.52 A

(c) 1.51 A

(d) 3.52 A

(iv) Power in primary coil is

(a) 20W

(b) 5W

(c) 10 W

(d) 15W

(v) Power in secondary coil is

(a) 15W

(b) 20 W

(c) 7W

(d) 8 W

When the frequency of ac supply is such that the inductive reactance and capacitive reactance become equal, the impedance of the series LCR circuit i equal to the ohmic resistance in the circuit. Such a series LCR circuit is known as resonant series LCR circuit and the frequency of the ac supply is known as resonant frequency
Resonance phenomenon is exhibited by a circuit only ifboth Land C are present in the circuit. We cannot have resonance in a RL or RC circuit
A series LCR circuit with \(L=0.12 \mathrm{H}, C=480 \mathrm{nF}, R=23 \Omega\) is connected to a 230 V variable frequency supply

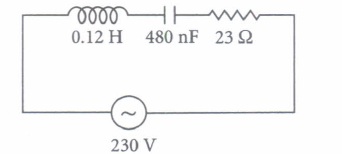
(i) Find the value of source frequency for which current amplitude is maximum

(a) 222.32 Hz

(b) 550.52 Hz

(c) 663.48 Hz

(d) 770 Hz

(ii) The value of maximum current is

(a) 14.14 A

(b) 22.52 A

(c) 50.25 A

(d) 47.41 A

(iii) The value of maximum power is

(a) 2200 W

(b) 2299.3 W

(c) 5500 W

(d) 4700 W

(iv) What is the Q-factor of the given circuit?

(a) 25

(b) 42.21

(c) 35.42

(d) 21.74

(v) At resonance which of the following physical quantity is maximum?

(a) Impedance

(b) Current

(c) Both (a) and (b)

(d) Neither (a) nor (b)

An LC circuit also called a resonant circuit, tank circuit or tuned circuit is an electric circuit consisting of an inductor represented by the letter L and a capacitor, represented by the letter C connected together. An LC circuit is an idealized model since it assumes there is no dissipation of energy due to resistance.
An LC circuit contains a 20 mH inductor and a \(50 \mu \mathrm{F}\) capacitor with an initial charge of 10 mC The resistance of the circuit is negligible. Let the instant the circuit is closed be t = 0.

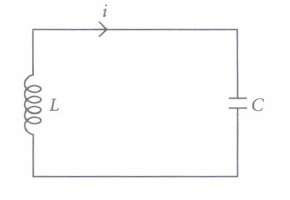
(i) The total energy stored initially is

(a) 5 J

(b) 3 J

(c) 10 J

(d) 1 J

(ii) The natural frequency of the circuit is

(a) 159.24 Hz

(b) 200.12 Hz

(c) 110.25 Hz

(d) 95 Hz

(iii) At what time is the energy stored completely electrical?

\(\text { (a) } T, 5 T, 9 T\)

\(\text { (b) } \frac{T}{2}, \frac{5 T}{2}, \frac{9 T}{2}\)

(c) 0, T, 2T, 3T

\(\text { (d) } 0, \frac{T}{2}, T, \frac{3 T}{2}\)

(iv) At what time is the energy stored completely magnetic?

\(\text { (a) } \frac{T}{2}, \frac{3 T}{2}, \frac{T}{4}\)

\(\text { (b) } \frac{T}{3}, \frac{T}{9}, \frac{T}{12}\)

(c) 0, 2T, 3T

\(\text { (d) } \frac{T}{4}, \frac{3 T}{4}, \frac{5 T}{4}\)

(v) The value of X_L is

\(\text { (a) } 20 \Omega\)

\(\text { (b) } 40 \Omega\)

\(\text { (c) } 60 \Omega\)

\(\text { (d) } 50 \Omega\)

Step-down transformers are used to decrease or step-down voltages. These are used when voltages need to be lowered for use in homes and factories.
A small town with a demand of 800 kW of electric power at 220 V is situated 15 km away from an electric plant generating power at 440 V. The resistance of the two wire line carrying power is \(0.5 \Omega\) per km. The town gets power from the line through a 4000 - 220 V step-down transformer at a sub-station in the town.

(i) The value of total resistance of the wires is

\(\text { (a) } 25 \Omega\)

\(\text { (b) } 30 \Omega\)

\(\text { (c) } 35 \Omega\)

\(\text { (d) } 15 \Omega\)

(ii) The line power loss in the form of heat is

(a) 550 kW

(b) 650 kW

(c) 600 kW

(d) 700 kW

(iii) How much power must the plant supply, assuming there is negligible power loss due to leakage?

(a) 600 kW

(b) 1600 kW

(c) 500 W

(d) 1400 kW

(iv) The voltage drop in the power line is

(a) 1700V

(b) 3000V

(d) 2800 V

(v) The total value of voltage transmitted from the plant is

(a) 500 V

(b) 4000 V

(c) 3000 V

(d) 7000 V

In an a.c. circuit, values of voltage and current change every instant. Therefore, power of an a.c. circuit at any instant is the product of instantaneous voltage (E) and instantaneous current (I). The average power supplied to a pure resistance R over a complete cycle of a.c. is \(P=E_{v} I_{v}\) When circuit is inductive, average power per cycle is \(E_{v} I_{v} \cos \phi\)

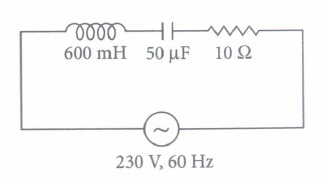
In an a.c. circuit, 600 mH inductor and a \(50 \mu \mathrm{F}\) capacitor are connected in series with \(10 \Omega\) nresistance. The a.c. supply to the circuit is 230 V, 60 Hz.
(i) The average power transferred per cycle to resistance is

(a) 10.42 W

(b) 15.25 W

(c) 17.42 W

(d) 13.45 W

(ii) The average power transferred per cycle to capacitor is

(a) zero

(b) 10.42 W

(c) 17.42 W

(d) 15W

(iii) The average power transferred per cycle to inductor is

(a) 25W

(b) 17.42 W

(c) 16.52 W

(d) zero

(iv) The total power transferred per cycle by all the three circuit elements is

(a) 17.42 W

(b) 10.45W

(c) 12.45 W

(d) zero

(v) The electrical energy spend in running, the circuit for one hour is

(a) 7.5 x 10⁵ Joule

(b) 10 x 10³ Joule

(c) 9.4 x 10³ Joule

(d) 6.2 x 10⁴Joule

A transformer is an electrical device which is used for changing the a.c. voltages. It is based on the phenomenon of mutual induction i.e. whenever the amount of magnetic flux linked with a coil changes, an e.m.f is induced in the neighbouring coil. For. an ideal transformer, the resistances of the primary and secondary windings are negligible.

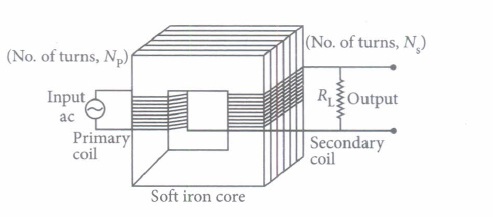
It can be shown that \(\frac{E_{s}}{E_{p}}=\frac{I_{p}}{I_{s}}=\frac{n_{s}}{n_{p}}=k\)
where the symbols have their standard meanings.
For a step up transformer \(n_{s}>n_{p} ; E_{s}>E_{p} ; k>1 ; \quad \therefore I_{s}
For a step down transformer \(n_{s}
The above relations are on the assumptions that efficiency of transformer is 100%.
lentlac ,effciency \(\eta=\frac{\text { output power }}{\text { intput power }}=\frac{E_{s} I_{s}}{E_{p} I_{p}}\)
(i) Which of the following quantity remains constant in an ideal transformer?

(a) Current

(b) Voltage

(c) Power

(d) All of these

(ii) Transformer is used to

(a) convert ac to dc voltage	(b) convert de to ac voltage
(c) obtain desired dc power	(d) obtain desired ac voltage and current

(iii) The number of turns in primary coil of a transformer is 20 and the number of turns in a secondary is 10. If the voltage across the primary is 220 ac V, what is the voltage across the secondary?

(a) 100 ac V

(b) 120 ac V

(c) 110 ac V

(d) 220 ac V

(iv) In a transformer the number of primary turns is four times that of the secondary turns. Its primary is connected to an a.c. source of voltage V. Then

(a) current through its secondary is about four times that of the current through its primary

(b) voltage across its secondary is about four times that of the voltage across its primary.

(c) voltage across its secondary is about two times that of the voltage across its primary

(d) voltage across its secondary is about \(\frac{1}{2 \sqrt{2}}\) times that of the voltage across its primary

(v) A transformer is used to light 100 W-110 V lamp from 220 V mains. If the main current is 0.5 A, the efficiency of the transformer is

(a) 95%

(b) 99%

(c) 90%

(d) 96%

The output of an a.c. generator in a power station is 5000 V.
A transformer increases the voltage to 115000 V before the electrical power is transmitted to a distant town.
(i) State and explain, using a relevant equation, one advantage of transmitting electrical power at high voltage.
(ii) The transformer contains two coils, the primary coil and secondary coil.
(a) State the other main component of a transformer and the material from which it is made.
(b) State the component in the transformer to which the a.c. generator is connected.
(c) If there are 500 turns in the primary of a coil of the transformer. Calculate the number of turns in the secondary coil.
(iii) Transformers within the town reduce the voltage to 220 V. Why?

*****************************************

Answers

Alternating Current Case Study Questions With Answer Key Answer Keys

Case Study

(i) (b):Given: \(R=12 \Omega, X_{C}=14 \Omega, L=0.1 \mathrm{H}\)
\(X_{L}=\omega L=2 \pi \cup L=2 \times 3.14 \times 50 \times 0.1=31.4 \Omega\)
(ii) (d): Impedance \(Z=\sqrt{R^{2}+\left(X_{L}-X_{C}\right)^{2}}\)
\(=\sqrt{(12)^{2}+(31.4-14)^{2}}=21.13 \Omega\)
(iii) (d): \(I_{v}=\frac{E_{v}}{Z}=\frac{200 \mathrm{~V}}{21.13}=9.46 \mathrm{~A}\)
(iv) (c): \(\tan \phi=\frac{X_{L}-X_{C}}{R}=\frac{31.4-14}{12}=1.45\)
\(\phi=\tan ^{-1}(1.45)=55^{\circ} 4^{\prime}\)
(v) (c)

(i) (c) :Ohm is the unit of capacitive reactance.
(ii) (a): Capacitive reactance \(X_{C}^{1}=\frac{1}{\omega C}=\frac{1}{2 \pi v C}\)
\(=\frac{1}{2 \pi \times 10^{6} \times 5 \times 10^{-6}}=0.032 \Omega\)
(iii) (b): In capacitive circuit, resistance to the flow of current is offered by the capacitor.
(iv) (b)
(v) (a): Current \(I_{v}=\frac{E_{v}}{X_{C}}=\frac{E_{v}}{1 / 2 \pi v C}=(2 \pi v C) E_{v}\)
\(I_{v}=2 \times 3.14 \times 50 \times 10^{-6} \times 200=6.28 \times 10^{-2} \mathrm{~A}\)

(i) (c) :Inductive reactance
\(X_{L}=\omega L=2 \pi v L=2 \pi \times 100 \times 14 \times 10^{-3}\)
\(X_{L}=8.8 \Omega\)
(ii) (b)
:(iii) (b) In an inductor voltage leads the current by \(\frac{\pi}{2}\) or current lags the voltage by \(\frac{\pi}{2}\).
(iv) (b): The current in the inductor coil is given by \(I_{0}=\frac{E_{0}}{X_{L}}=\frac{\sqrt{2} E_{v}}{2 \pi v L}\)
\(L=\frac{\sqrt{2} E_{v}}{2 \pi v I_{0}}=\frac{1.414 \times 200}{2 \times 3.14 \times 50 \times 0.9}=1 \mathrm{H}\)
(v) (a): Inductive reactance
\(X_{L}=\omega L=2 \pi v L=2 \times 3.14 \times 50 \times 2=628 \Omega\)
\(I_{0}=\frac{E_{0}}{X_{L}} \Rightarrow I_{0}=\frac{\sqrt{2} \times E_{v}}{X_{L}}=\frac{\sqrt{2} \times 150}{628}=0.337 \mathrm{~A}\)

(I) (b): Inductance, L = 80 mH = 80 x 10^-3 H
Capacitance, C = \(60 \mu \mathrm{F}=60 \times 10^{-6} \mathrm{~F}, V=230 \mathrm{~V}\)
Frequency, u = 50 Hz
\(\omega=2 \pi v=100 \pi \mathrm{rad} \mathrm{s}^{-1}\)
Peak voltage \(V_{0}=V \sqrt{2}=230 \sqrt{2} \mathrm{~V}\)
Maximum current is given by, \(I_{0}=\frac{V_{0}}{\left(\omega L-\frac{1}{\omega C}\right)}\)
\(I_{0}=\frac{230 \sqrt{2}}{\left(100 \pi \times 80 \times 10^{-3}-\frac{1}{100 \pi \times 60 \times 10^{-6}}\right)}\)
Amplitude of maximum current, I_o = 11.63 A
(ii) (c): rms value of current,
\(I=\frac{I_{0}}{\sqrt{2}}=\frac{-11.63}{\sqrt{2}}=-8.23 \mathrm{~A}\)
Negative sign appears as \(\omega L<\frac{1}{\omega C}\)
(iii) (a): Average power consumed by the inductor is zero because of phase difference of \(\frac{\pi}{2}\) between voltage and current through inductor.
(iv) (b): Average power consumed by the capacitor is zero because of phase difference of \(\frac{\pi}{2}\) between voltage and current through capacitor
(v) (a)

(i) (c) : As \(\frac{E_{s}}{E_{p}}=\frac{n_{s}}{n_{p}} \Rightarrow E_{s}=E_{p} \cdot \frac{n_{s}}{n_{p}}\)
\(=\frac{120 \times 50}{2000}=3 \mathrm{~V}\)
(ii) (d) : \(I_{s}=\frac{E_{s}}{R} \Rightarrow I_{s}=\frac{3}{0.6}=5 \mathrm{~A}\)
(iii) (a) : As \(\frac{I_{p}}{I_{s}}=\frac{E_{s}}{E_{p}}\)
\(\Rightarrow I_{p}=\frac{E_{s}}{E_{p}} \times I_{s}=\frac{\ 3}{120} \times 5=0.125 \mathrm{~A}\)
(iv) (d) : Power in primary \(P_{p}=E_{p} \times I_{p}=120 \times 0.125\)
= I5W
(v) (a) : Power in secondary coil \(P_{s}=E_{s} \times I_{s}=3 \times 5\)
= 15W

(i) (c) : Here \(L=0.12 \mathrm{H}, C=480 \mathrm{nF}^{\prime}=480 \times 10^{-9} \mathrm{~F}\)
\(R=23 \Omega, V=230 \mathrm{~V}\)
\(V_{0}=\sqrt{2} \times 230=325.22 \mathrm{~V}\)
\(I_{0}=\frac{V_{0}}{\sqrt{R^{2}+\left(\omega L-\frac{1}{\omega C}\right)^{2}}}\)
At resonance, \(\omega L-\frac{1}{\omega C}=0\)
\(\omega=\frac{1}{\sqrt{L C}}=\frac{1}{\sqrt{0.12 \times 480 \times 10^{9}}}=4166.67 \mathrm{rad} \mathrm{s}^{-1}\)
\(v_{R}=\frac{4166.67}{2 \times 3.14}=663.48 \mathrm{~Hz}\)
(ii) (a) : Current \(I_{0}=\frac{V_{0}}{R}=\frac{325.22}{23}=14.14 \mathrm{~A}\)
(iii) (b) : Maximum power \(P_{\max }=\frac{1}{2}\left(I_{0}\right)^{2} R\)
\(=\frac{1}{2} \times(14.14)^{2} \times 23=2299.3 \mathrm{~W}\)
(iv) (d) : Quality factor \(Q=\frac{X_{L}}{R}=\frac{\omega_{r} L}{R}\)
\(=\frac{4166.67 \times 0.12}{23}=21.74\)
(v) (b)

(i) (d):Energy, \(E=\frac{1}{2} \frac{Q^{2}}{C}=\frac{\left(10 \times 10^{-3}\right)^{2}}{2 \times 50 \times 10^{-6}}=1 \mathrm{~J}\)
(ii) (a): Frequency \(v=\frac{1}{2 \pi \sqrt{L C}}\)
\(=\frac{1}{2 \pi \sqrt{20 \times 10^{-3} \times 50 \times 10^{-6}}}=\frac{10^{3}}{2 \pi}=159.24 \mathrm{~Hz}\)
(iii) (d): Total time period \(T=\frac{1}{v}=\frac{1}{159.24}=6.28 \mathrm{~ms}\)
Total charge on capacitor at time t \(Q^{\prime}=Q \cos \frac{2 \pi}{T} t\)
For energy stored is electrical, we can write \(Q^{\prime}=\pm Q\)
Hence, energy stored in the capacitor is completely electrical at \(t=0, \frac{T}{2}, T, \frac{3 T}{2}, \ldots .\)
(iv) (d): Magnetic energy is maximum when electrical energy is equal to zero
Hence \(t=\frac{T}{4}, \frac{3 T}{4}, \frac{5 T}{4}\)
(v) (a): \(X_{L}=\omega L=2 \pi \cup L=2 \times 3.14 \times 159.24 \times 20\) x 10^-3
\(\Rightarrow \quad X_{L}=20 \Omega\)

(i) (d): Resistance of the two wire lines carrying power \(=0.5 \Omega / \mathrm{km}\)
Total resistance \(=(15+15) 0.5=15 \Omega\)
(ii) (c): Line power loss = I²R
RMS current in the coil,
\(I=\frac{P}{V_{1}}=\frac{800 \times 10^{3}}{4000}=200 \mathrm{~A}\)
\(\therefore\) Power loss \(=(200)^{2} \times 15=600 \mathrm{~kW}\)
(iii) (d): Assuming that the power loss is negligible due to the leakage of the current.
The total power supplied by the plant
= 800 kW + 600 kW = 1400 kW
(iv) (b): Voltage drop in the power line = IR
= 200 x 15 = 3000 V
(v) (d): Total voltage transmitted from the plant = 3000 V + 4000 V = 7000 V

(i) (c): Average power transferred per cycle to resistance is \(P_{v}=I_{v}^{2} R\)
As \(X_{L}=\omega L=2 \pi \cup L=2 \times \frac{22}{7} \times 60 \times 0.6=226.28 \Omega\)
\(X_{C}=\frac{1}{\omega C}=\frac{1}{2 \pi v C}=\frac{1}{2 \times 22 / 7 \times 60 \times 50 \times 10^{-6}}\)
\(=53.03 \Omega\)
\(Z=\sqrt{R^{2}+\left(X_{L}-X_{C}\right)^{2}}\)
\(=\sqrt{(10)^{2}+(226.28-53.03)^{2}}=173.53 \Omega\)
\(I_{v}=\frac{E_{v}}{Z}=\frac{230}{173.53}=1.32 \mathrm{~A}\)
\(P_{v}=I_{v}^{2} R=(1.32)^{2} \times 10=17.42 \mathrm{~W}\)
(ii) (a) : \(P_{C}=E_{v} I_{v} \cos \phi\)
In a capacitor, phase difference \(\phi=90^{\circ}\)
\(\therefore \quad P_{L}=E_{v} I_{v} \cos 90^{\circ}=\text { zero }\)
(iii) (d): \(P_{L}=E_{\gamma} I_{v} \cos \phi\)
In an inductor, phase difference \(\phi=90^{\circ}\)
\(P_{L}=E_{\nu} I_{v} \cos 90^{\circ}=\text { zero }\)
(iv) (a): Total power absorbed per cycle
\(P=P_{R}+P_{C}+P_{L}=17.42+0+0=17.42 \mathrm{~W}\)
(v) (d): Energy spent = power x time
\(=17.42 \times 60 \times 60=6.2 \times 1,0^{4} \text { Joule }\)

(i) (c) :In an ideal transformer, there is no power loss. The efficiency of an ideal transformer is \(\eta=1(i . e\) 100%) i.e. input power = output power.
(ii) (d): Transformer is used to obtain desired ac voltage and current.
(iii) (c): For a transformer \(\frac{V_{s}}{V_{p}}=\frac{N_{s}}{N_{p}}\)
where Ndenotes number of turns and V = voltage
\(\therefore \frac{V_{s}}{220}=\frac{10}{20} \quad \therefore V_{s}=110 \mathrm{ac} \mathrm{V}\)
(iv) (a): In a transformer the primary and secondary currents are related by
\(I_{s}=\left(\frac{N_{p}}{N_{s}}\right) I_{p}\)
and the voltages are related by
\(V_{s}=\left(\frac{N_{s}}{N_{p}}\right) V_{p}\)
where subscripts p and s refer to the primary and secondary of the transformer
Here, \(V_{p}=V, \frac{N_{p}}{N_{s}}=4 \quad \therefore \quad I_{s}=4 I_{p}\)
and \(V_{s}=\left(\frac{1}{4}\right) V=\frac{V}{4}\)
(v) (c): The efficiency of the transformer is \(\eta=\frac{\text { Output power }\left(P_{\text {out }}\right)}{\text { Input power }\left(P_{\text {in }}\right)} \times 100\)
Here, \(P_{\text {out }}=100 \mathrm{~W}, P_{\text {in }}=(220 \mathrm{~V})(0.5 \mathrm{~A})=110 \mathrm{~W}\)
\(\therefore \quad \eta=\frac{100 \mathrm{~W}}{110 \mathrm{~W}} \times 100 \approx 90 \%\)

(i) \(\because\) P = V.I or I ²R
On increasing voltage, electric current reduces, therefore less power/energy is lost (as P \(\alpha\) I²) in cables during transmission.
(ii) (a) laminated iron core
(b) A.C. generator is connected to primary coil
(c) \(N_{S}=N_{P} \times \frac{V_{S}}{V_{P}}=500 \times \frac{115000}{5000}\)
N_s= 11500 turns
(iii) Transmission of 220 V
(a) needed less insulation
(b) is safer
(c) devices are designed for 220 V.

Tags: CBSE 12th Physics Case Study Questions, 12th Physics Important Case study Questions, 12th Physics Case study Questions, Case study Questions 12th Physics, 12th Physics Case Study Questions, 12th Std Physics Case Study Questions with Answers, CBSE 12th Physics Questions, CBSE Physics Case Study Questions with Solutions, Class 12th Physics Case Study Questions with Solutions, Case Study Questions and Answers 12th Physics, Physics - Alternating CurrentCase Study Questions, 12th Physics Case Study Questions, Physics Important Questions 12th, +2 Case Study Questions, 12 Physics Important Case Study Questions, 12th case study questions with answers, cbse 12th Physics Important case study Questions, 2022 Syllabus 12th Physics Case study Questions, Physics case study questions 2022, Current syllabus 12th Physics case study questions, 12th Physics case study questions with Answer Key 2022, Alternating Current case study Questions 12th Physics, 12th Study Materials, 12th Physics Study Materials, Case study Questions.