Class 12th Physics - Dual Nature of Radiation and Matter Case Study Questions and Answers 2022 - 2023
By QB365 on 09 Sep, 2022
QB365 provides a detailed and simple solution for every Possible Case Study Questions in Class 12th Physics Subject - Dual Nature of Radiation and Matter, CBSE. It will help Students to get more practice questions, Students can Practice these question papers in addition to score best marks.
QB365 - Question Bank Software
Dual Nature of Radiation and Matter Case Study Questions With Answer Key
12th Standard CBSE
-
Reg.No. :
Physics
-
Photoelectric effect is the phenomenon of emission of electrons from a metal surface, when radiations of suitable frequency fallon them. The emitted electrons are called photoelectrons and the current so produced is called photoelectric current.
(i) With the increase of intensity of incident radiations on photoelectrons emitted by a photo tube, the number of photoelectrons emitted per unit time is(a) increases (b) decreases (c) remains same (d) none of these (ii) It is observed that photoelectron emission stops at a certain time t after the light source is switched on. The stopping potential (V) can be represented as
(a) 2(KEmax/e) (b) (KEmax/e) (c) (KEmax/3e) (d) (KEmax/2e) (iii) A point source of light of power 3.2 x 10-3 W emits monoenergetic photons of energy 5.0 eV and work function 3.0 eV. The efficiency of photoelectron emission is 1 for every 106 incident photons. Assume that photoelectrons are instantaneously swept away after emission. The maximum kinetic energy of photon is
(a) 4 eV (b) 5 eV (c) 2 eV (d) Zero (iv) Which of the following device is the application of Photoelectric effect?
(a) Light emitting diode (b) Diode (c) Photocell (d) Transistor (v) If the frequency of incident light falling on a photosensitive metal is doubled, the kinetic energy of the emitted photoelectron is
(a) unchanged (b) halved (c) doubled (d) more than twice its initial value (a) -
When a monochromatic radiations of suitable frequency obtained from source S, after being filtered by a filter attached on the window W, fall on the photosensitive place C, the photo electrons are emitted from C, which get accelerated towards the plate A if it is kept at positive potential. These electrons flow in the outer circuit resulting in photoelectric current. Due to it, the micro ammeter shows a deflection. The reading of micrommeter measures the photoelectric current.
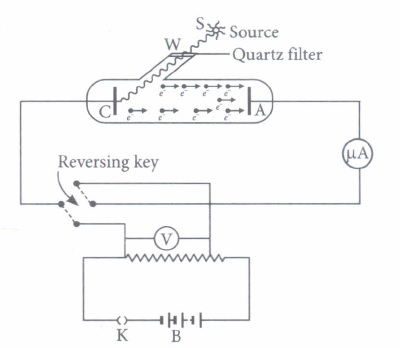
An experimental setup of verification of photoelectric effect is shown in figure. The voltage across the electrodes is measured with the help of an ideal voltmeter, and which can be varied by moving jockey J on the potentiometer wire. The battery used in potentiometer circuit is of 16 V and its internal resistance is 2 \(\Omega\) The resistance of 100 ern long po.t•e. ntiometer wire is 8 \(\Omega\).
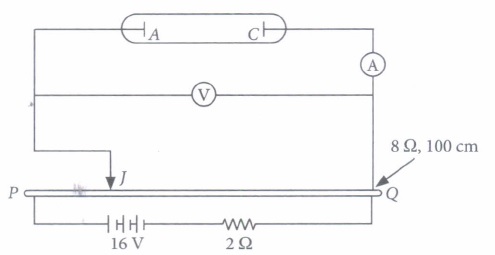
The photocurrent is measured with the help of an ideal ammeter. Two plates of potassium oxide of area 50 cm2 at separation 0.5 mm are used in the vacuum tube. Photocurrent in the circuit is very small, so we can treat the
potentiometer circuit as an independent circuitLight Violet blue Green Yellow Orange Red \(\lambda\) in \(\dot A\) 4000-5000 4500-5000 5000-5500 5500-6000 6000-6500 6500-7000 (i) When radiation falls on the cathode plate, a current of 2 \(\mu \)A is recorded in the ammeter. Assuming that the vacuum tube setup follows Ohm's law, the equivalent resistance of vacuum tube operating in the case when jockey is at end P is
(a) 8 x 108\(\Omega\) (b) 16 x 106\(\Omega\) (c) 8 x 106\(\Omega\) (d) 10 x 106\(\Omega\) (ii) It is found that ammeter current remains unchanged (2 \(\mu\)A) even when the jockey is moved from the end P to the middle point of the potentiometer wire. Assuming that all the incident photons eject electrons and the power of the light incident is 4 x 10-6\(\Omega\)Then, the color of the incident light is
(a) Green (b) Violet (c) Red (d) Orange (iii) Which of the following colors may not give photoelectric effect for this cathode?
(a) Green (b) Violet (c) Red (d) Orange (iv) When other light falls on the anode plate, the ammeter reading zero till jockey is moved from the end P to the middle point of the wire PQ. Therefore, the deflection is recorded in the ammeter. The maximum kinetic energy of the emitted electron is
(a) 16 eV (b) 8 eV (c) 4 eV (d) 10 eV (v) If the intensity of incident radiation is increased twice, the number of photoelectrons emitted per second will be
(a) halves (b) double (c) remain same (d) four times (a) -
A point source S of power 6.4 x 10-3W emits mono energetic photons each of energy 6.0 eV. The source is located at a distance of 0·8 m from the centre of a stationary metallic sphere of work function 3·0 eV and of radius 1.6 x 10-3 m as shown in figure. The sphere is isolated and initially neutral and photoelectrons are instantly taken away from sphere after emission. The efficiency of photoelectric emission is one for very 105 incident photons.
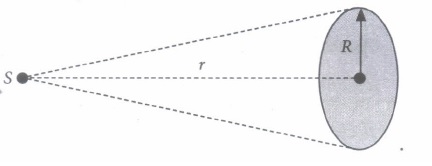
(i) The'power received by the sphere through radiations is\(\text { (a) } \frac{4 R^{2}}{P r}\) \(\text { (b) } \frac{P R^{2}}{4 r^{2}}\) \(\text { (c) } \frac{p^{2} R}{2 \pi r}\) \(\text { (d) } \frac{P R}{4 r}\) (ii) Number of photons striking the metal sphere per second is
(a) 6.7 x 109 (b) 3.3 x 109 (c) 6.7 x 1010 (b) 3.3 x 1010 (iii) The number of photoelectrons emitted per second is about
(a) 3.3 x 104 (b) 6.7 x 104 (c) 6.7 x 1015 (d) 3.3 x 1015 (iv) The photoelectric emission stops when the sphere acquires a potential about
(a) 2 V (b) 3 V (c) 4 V (d) 6 V (v) If the distance of source becomes double from the centre of the metal sphere then the power received by the sphere
\(\text { (a) } \frac{P R^{2}}{4 r^{2}}\) \(\text { (b) } \frac{P R^{2}}{16 r^{2}}\) \(\text { (c) } \frac{P R^{2}}{4 r}\) \(\text { (d) } \frac{P^{2} R^{2}}{16 r^{2}}\) (a) -
According to Einstein, when a photon of light of frequency u or wavelength \(\lambda\) is incident on a photosensitive metal surface of work function \(\phi\)0w' here \(\phi\)0< hv (here, h is Planck's constant), then the emission of photoelectrons takes place. The maximum kinetic energy of the emitted photoelectrons is given by Kmax = hv - \(\phi\)0. If the frequency of the incident light is V0 called threshold frequency, the photoelectrons are emitted from metal without any kinetic energy. So hv0 = \(\phi\)
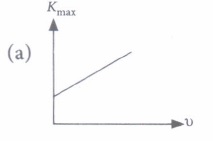
(i) A metal of work function 3·3 eV is illuminated by light of wavelength 300 nm. The maximum kinetic energy of photoelectrons emitted is (taking h = 6·6 x 10-34 Js)(a) 0.413 eV (b) 0.825 eV (c) 1.65 eV (d) 1.32 eV (ii) The variation of maximum kinetic energy (Kmax) of the emitted photoelectrons with frequency (v) of the incident radiations can be represented by
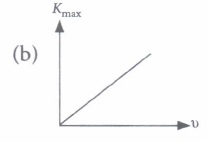
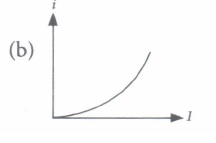
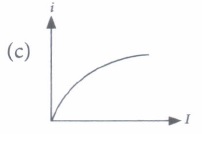
(iii) The variation of photoelectric current (i) with the intensity of the incident radiation (I) can be represented by
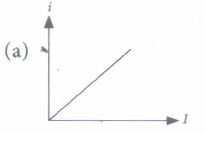
(iv) The graph between the stopping potential (V0) and \(\left(\frac{1}{\lambda}\right)\) is shown in the figure \(\phi_{1}, \phi_{2}, \phi_{3}\) 3 are work function. Which of the following options is correct?
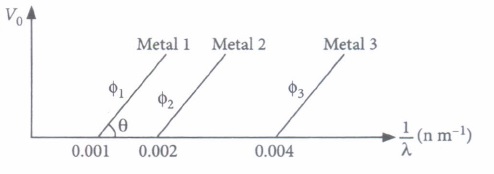
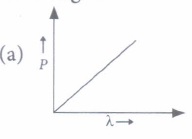
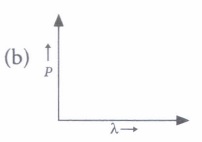
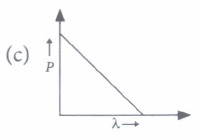
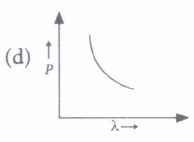
\(\text { (a) } \phi_{1}: \phi_{2}: \phi_{3}=1: 2: 3\)\(\text { (b) } \phi_{1}: \phi_{2}: \phi_{3}=4: 2: 1\) \(\text { (c) } \phi_{1}: \phi_{2}: \phi_{3}=1: 2: 4\) (d) Ultraviolet light can be used to emit photoelectrons from metal 2 and metal 3 only (v) Which of the following figures represent the variation of particle momentum and the associated de- Broglie wavelength?
 (a)
(a) -
When light of sufficiently high frequency is incident on a metallic surface, electrons are emitted from the metallic surface. This phenomenon is called photoelectric emission. Kinetic energy of the emitted photoelectrons depends on the wavelength of incident light and is independent of the intensity of light. Number of emitted photoelectrons depends on intensity. (hv - \(\phi\) is the maximum kinetic energy of emitted photoelectrons (where \(\phi\) is the work function of metallic surface). Reverse effect of photo emission produces X-ray. X-ray is not deflected by electric and magnetic fields. Wavelength of a continuous X-ray depends on potential difference across the tube. Wavelength of characteristic X-ray depends on the atomic number.
(i) Einstein's photoelectric equation is\(\text { (a) } E_{\max }=h v-\phi\) \(\text { (b) } E=m c^{2}\) \(\text { (c) } E^{2}=p^{2} c^{2}+m_{0}^{2} c^{4}\) \(\text { (d) } E=\frac{1}{2} m v^{2}\) (ii) Light of wavelength \(\lambda\) which is less than threshold wavelength is incident on a photosensitive material. If incident wavelength is decreased so that emitted photoelectrons are moving with some velocity then stopping potential will
(a) increase (b) decrease (c) be zero (d) become exactly half (iii) When ultraviolet rays incident on metal plate then photoelectric effect does not occur, it occur by incident of
(a) Infrared rays (b) X-rays (c) Radio wave (d) Micro wave (iv) If frequency (v > v0) of incident light becomes n times the initial frequency (v), then K.E. of the emitted photoelectrons becomes (v0 threshold frequency).
(a) n times of the initial kinetic energy (b) More than n times of the initial kinetic energy (c) Less than n times of the initial kinetic energy (d) Kinetic energy of the emitted photoelectrons remains unchanged (v) A monochromatic light is used in a photoelectric experiment. The stopping potential
(a) Is related to the mean wavelength (b) Is related to the shortest wavelength (c) Is not related to the minimum kinetic energy of emitted photoelectrons (d) Intensity of incident light (a) -
If we allow radiations of a fixed frequency to fall on plate and the accelerating potential difference between the two electrodes is kept fixed, then the photoelectric current is found to increase linearly with the intensity of incident radiation. Here, radiation pressure is P = \(\left(\frac{1+e}{C}\right) I\). As, atmosphere pressure at sea level is 105Pa. If the intensity of light of a given wavelength, is increased, there is an increase in the number of photons incident on a given area in a given time. But the energy of each photon remain the same.
(i) The number of photons hitting the cone second\(\text { (a) } \pi R^{2} I / 2 E\) \(\text { (b) } 2 \pi R^{2} I / E\) \(\text { (c) } \pi R^{2} I / 4 E\) \(\text { (d) } \pi R^{2} I / E\) (ii) A radiation of energy E falls normally on a perfect reflecting surface. The momentum transferred to the surface is
\(\text { (a) } \frac{E}{c}\) \(\text { (b) } \frac{2 E}{c}\) \(\text { (c) } E c\) \(\text { (d) } \frac{E}{c^{2}}\) (iii) Which one is correct?
\(\text { (a) } E^{2}=p^{2} c^{2}\) \(\text { (b) } E^{2}=p^{2} c\) \(\text { (c) } E^{2}=p^{2}\) \(\text { (d) } E^{2}=\frac{p^{2}}{c^{2}}\) (iv) The incident intensity on a horizontal surface at sea level from the Sun is about 1 k W m-2. Assuming that 50% of this intensity is reflected and 50% is absorbed, determine the radiation pressure on this horizontal surface.
(a) 8.2 x 10-2 Pa (b) 5 x 10-6 Pa (c) 3 x 10-5 Pa (d) 6 x 10-5 Pa (v) Find the ratio of radiation pressure to atmospheric pressure P0 about 1 x 105 Pa at sea level.
(a) 5 x 10-11 (b) 4 x 10-8 (c) 6 x 10-12 (d) 8 x 10-11 (a) -
According to de-Broglie, a moving material particle sometimes acts as a wave and sometimes as a particle or a wave associated with moving material particle which controls the particle in every respect. The wave associated with moving particle is called matter wave or de-Broglie wave where wavelength called de-Broglie wavelength is given by \(\lambda=\frac{h}{m v}\)
(i) If a proton and an electron have the same de Broglie wavelength, then(a) kinetic energy of electron < kinetic energy of proton (b) kinetic energy of electron = kinetic energy of proton (c) momentum of electron = momentum of proton (d) momentum of electron < momentum of proton (ii) Which of these particles having the same kinetic energy has the largest de Broglie wavelength?
(a) Electron (b) Alpha particle (c) Proton (d) Neutron (iii) Two particles A1 and A2 of masses m1 m2 (m1 > m2) have the same de Broglie wavelength. Then
(a) their momenta are the same. (b) their energies are the same. (c) momentum of A1 is less than the momentum of A2. (d) energy of A1 is more than the energy of A2. (iv) When the velocity of an electron increases, its de Broglie wavelength
(a) increases (b) decreases (c) remains same (d) may increase or decrease (v) Proton and a-particle have the same de-Broglie wavelength. What is same for both of them?
(a) time period (b) energy (c) frequency (d) momentum (a) -
According to wave theory, the light of any frequency can emit electrons from metallic surface provided the intensity of light be sufficient to provided necessary energy for emission of electrons, but according to experimental observations, the light of frequency less than threshold frequency can not emit electrons; whatever be the intensity of incident light. Einstein also proposed that electromagnetic radiation is quantised.If photoelectrons are ejected from a surface when light of wavelength \(\lambda\) 1= 550 nm is incident on it. The stopping potential for such electrons is Vs = 0.19 V. Suppose the radiation of wavelength \(\lambda\)2= 190 nm is incident on the surface.
(i) Photoelectric effect supports quantum nature oflight because
(A) there is a minimum frequency of light below which no photoelectrons are emitted.
(B) the maximum K.E. of photoelectric depends only on the frequency of light and not on its intensity.
(C) even when the metal surface is faintly illuminated, the photo electrons leave the surface immediately.
(D) electric charge of the photoelectrons is quantized.(a) A,B,C (b) B,C (c) C,D (d) A,D,C (ii) In photoelectric effect, electrons are ejected from metals, if the incident light has a certain minimum
(a) wavelength (b) frequency (c) amplitude (d) angle of incidence (iii) Calculate the stopping potential VS2of surface.
(a) 4.47 (b) 3.16 (c) 2.76 (d) 5.28 (iv) Calculate the work function of the surface.
(a) 3.75 (b) 2.07 (c) 4.20 (d) 3.60 (v) Calculate the threshold frequency for the surface.
(a) 500 x 1012 Hz (b) 480 x 1013 Hz (c) 520 x 1011Hz (d) 460 x 1013 Hz (a) -
The photon picture of electromagnetic radiations and the characteristic properties of photons are as follows:In the interaction of radiation with matter, radiation behaves as if it is made of particles like photons. Each photon has energy \(E(=h v=h c / \lambda)\) and momentum \(p\left(=\frac{h v}{c}=\frac{h}{\lambda}\right)\) where h is Planck's constant, v and A are the frequency and wavelength of radiation and c is the velocity of light. The photon energy is independent of the intensity of radiations. All the photons emitted from a source of radiations travel through space with the same speed c. The frequency of photon gives the radiation, a definite energy (or colour) which does not change when photon travels through different media. Photons are not deflected by electric and magnetic fields. This shows that photons are electrically neutral.
(i) Which one among the following shows particle nature of light?(a) Photoelectric effect (b) Interference (c) Refraction (d) Polarization (ii) Which of the following statements about photon is incorrect?
(a) Photons exert no pressure (b) Momentum of photon is \(\frac{h v}{c}\) (c) Rest mass of photon is zero (d) Energy of photon is hv (iii) The rest mass of photon is
\(\text { (a) } \frac{h v}{c}\) \(\text { (b) } \frac{h v}{c^{2}}\) \(\text { (c) } \frac{h v}{\lambda}\) (d) zero (iv) In a photon-particle collision (such as photon-electron collision), which of the following may not be conserved?
(a) Total energy (b) Number of photons (c) Total momentum (d) Both (a) and (b) (v) 'n' photons of wavelengt '\(\lambda\)' are absorbed by a black body of mass 'm'. The momentum gained by the body is
\(\text { (a) } \frac{h}{m \lambda}\) \(\text { (b) } \frac{m n h}{\lambda}\) \(\text { (c) } \frac{n h}{m \lambda}\) \(\text { (d) } \frac{n h}{\lambda}\) (a) -
To study photoelectric effect, an emitting electrode C of a photosensitive material is kept at negative potential and collecting electrode A is kept at positive potential in an evacuated tube. When light of sufficiently high frequency falls on emitting electrode, photoelectrons are emitted which travel directly to collecting electrode and hence an electric cusrent called photoelectric current starts flowing in the circuit, which is directly proportional to the number of photoelectrons emitted by emitting electrode C.

While demonstrating the existence of electromagnetic waves, Hertz found that high voltage sparks passed across the metal electrodes of the detector loop more easily when the cathode was illuminated by ultraviolet light from an arc lamp. The ultraviolet light falling on the metal surface caused the emission of negatively charged particles,which are now known to be electrons, into the surrounding space and hence enhanced the high voltage sparks.
(i) Cathode rays were discovered by(a) Maxwell Clerk James (b) Heinrich Hertz (c) William Crookes (d) J. J. Thomson (ii) Cathode rays consists of
(a) photons (b) electrons (c) pistons (d) a-particles. (iii) Who discovered the charge on an electron for the frist time?
(a) Millikan (b) Thomson (c) Kelvin (d) Coulomb (iv) The dual nature of light is exhibited by
(a) diffraction and photoelectric effect (b) photoelectric effect (c) refraction and interference (d) diffraction and reflection (v) In the phenomenon of electric discharge through gases at low pressure, the coloured glow in the tube appears as a result of
(a) collisions between the charged particles emitted from the cathode and the atoms of the gas (b) collision between different electrons of the atoms of the gas (c) excitation of electrons in the atoms (d) collision between the atoms of the gas. (a) -
In the investigation of "Photoelectric effect", light is incident on electrode A. This electrode A, along with electrode B is placed inside a vacuum tube diode. These electrodes are made from same metal and are connected to a microammeter and a variable voltage supply. Light enters vacuum tube through a window. With the help of filters, wavelength of light entering the window can be changed.
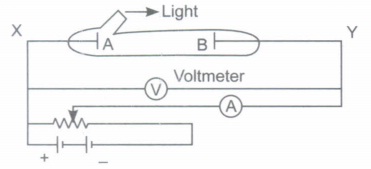
The data has been obtained from such an experimentWavelength (nm) 589 552 330 285 P.D (V) -0.246 -0.367 -1.870 -2.463 (i) Why must negative potential be applied to electrode B to stop the flow of electrical current?
(ii) Plot a suitable graph to determine Planck's constant h and the minimum energy \(\phi\) in S.I. units.(a)
Case Study
*****************************************
Answers
Dual Nature of Radiation and Matter Case Study Questions With Answer Key Answer Keys
-
(i) (a): With the increase of intensity of the incident radiation the number of photoelectrons emitted per un't time increases.
(ii) (b): As eV = KEmax
\(\therefore \quad V=\left(\frac{K E_{\max }}{e}\right)\)
(iii) (c) : From Einstein's photoelectric equation,
\(K E_{m a x}=h v-\phi=(5-3)=2 \mathrm{eV}\)
(iv) (c): A photocell is a technological application of the photoelectric effect.
(v) (d): According to Einstein's photoelectric equation, the kinetic energy of the emitted photoelectron is
\(K=h v-\phi_{n}\)
where v is the frequency of incident radiation and \(\phi\)0 is a work function of the metal.If the frequency of incident radiation is doubled, then
\(K^{\prime}=2 h v-\phi_{0}=2\left(h v-\phi_{0}\right)+\phi_{0}=2 K+\phi_{0}\) (Using (i))
\(K^{\prime}>2 K\) -
(i) (c) :Equivalent resistance
\(R=\frac{V}{I}=\frac{16 \mathrm{~V}}{2 \times 10^{-6} \mathrm{~A}}=8 \times 10^{6} \Omega\)
(ii) (d): \(P=\frac{I h C}{e \lambda}\)
\(\lambda=\frac{\left(2 \times 10^{-6}\right)\left(6.6 \times 10^{-34}\right)\left(3 \times 10^{8}\right)}{\left(4 \times 10^{-6}\right)\left(1.6 \times 10^{-19}\right)}\)
\(=\frac{9.9}{1.6} \times 10^{-7} \mathrm{~m}=\frac{9900}{1.6} \dot A=6187 \dot A\)
Which is in the range of orange light
(iii) (c) : The range of wavelength for red light is beyond the wavelength of incident light.
(iv) (b): Stopping potential, \(V_{s}=8 \mathrm{~V}\)
and \(\mathrm{K.E.}=e V_{\mathrm{s}}\)
\(\therefore \quad \mathrm{K} . \mathrm{E} .=8 \mathrm{eV}\)
(v) (b): Photoelectric current varies linearly with the intensity of the incident radiation. -
(i) (b): Let R be the radius of the metallic sphere and r be its distance from the source S0. The power received at the sphere is
\(P^{\prime}=\frac{P \times \pi R^{2}}{4 \pi r^{2}}=\frac{P R^{2}}{4 r^{2}}\)
(ii) (a): Number of photons striking the metal sphere per second is
\(n^{\prime}=\frac{P^{\prime}}{E}=\frac{6 \cdot 4 \times 10^{-9}}{6 \cdot 0 \times 1 \cdot 6 \times 10^{-19}}=6 \cdot 7 \times 10^{9} \mathrm{~s}^{-1}\)
(iii) (b): Number of photoelectrons emitted from metal sphere,\(\frac{n^{\prime}}{10^{5}}=\frac{6 \cdot 7 \times 10^{-9}}{10^{5}}=6 \cdot 7 \times 10^{4}\)
(iv) (b): Kinetic energy of the fastest photoelectrons is \(K_{\max }=6 \cdot 0-3 \cdot 0=3 \cdot 0 \mathrm{eV}\)
\(\therefore \text { Stopping potential, } V_{s}=\frac{K_{\max }}{e}=\frac{3 \cdot 0 \mathrm{eV}}{e}=3.0 \mathrm{~V}\)
(v) (b): When r = 2r, then power received by the sphere
\(P^{\prime \prime}=\frac{P \pi R^{2}}{4 \pi(2 r)^{2}}=\frac{1}{4}\left(\frac{P R^{2}}{4 r^{2}}\right)\) -
(i) (b): \(K_{\max }=h v-\phi_{0}=\frac{h c}{\lambda}-\phi_{0}\)
\(=\frac{\left(6 \cdot 6 \times 10^{-34}\right) \times\left(3 \times 10^{8}\right)}{\left(300 \times 10^{-9}\right) \times\left(1 \cdot 6 \times 10^{-19}\right)}-3 \cdot 3\)
\(=4 \cdot 125 \times 3 \cdot 3=0 \cdot 825 \mathrm{eV}\)
(ii) (c) : \(K_{\max }=h v-\phi_{0}, \text { When } v=v_{0}, K_{\max }=0\)
\(\therefore \quad 0=h v_{0}-\phi_{0} \text { or } \phi_{0}=h v_{0}\)
If v < v0 then Kmax is negative, i.e., no photoelectric emission takes place. Thus, graph (c) is possible.
(iii) (a): Photoelectric current (i) is proportional to the intensity of the emission light. Thus, graph (a) is possible.
(iv) (c): From Einstein's photoelectric equation,
\(K_{\max }=e V_{0}=\frac{h c}{\lambda}-\phi\)
or \(V_{0}=\frac{h c}{e} \cdot \frac{1}{\lambda}-\frac{\phi}{e}\)
Graph of V0 versus \(\frac{1}{\lambda}\) is a straight line Slope of straight line,\(\tan \theta=\frac{h c}{e}\)
\(\text { At } V_{0}=0, \text { we have }\)
\(\phi_{1}: \phi_{2}: \phi_{3}=\frac{h c}{\lambda_{01}}: \frac{h c}{\lambda_{02}}: \frac{h c}{\lambda_{03}}\)
\(0.001 h c: 0.002 h c: 0.004 h c\)
\(\therefore 1: 2: 4\)
(v) (d): de-Broglie wavelength
\(\lambda=\frac{h}{p} i . e ., \lambda \propto \frac{1}{p}\)
So the graph between \(\lambda\) and P is of the type shown is option (d). -
(i) (a)
(ii) (a): According to Einstein's photoelectric equation,
\(e V_{0}=\frac{h c}{\lambda}-\frac{h c}{\lambda_{0}}\)
As \(\lambda\)0 is constant, so when \(\lambda\). is decreased, stopping potential (V0) increases.
(iii) (b): It indicates that threshold frequency is greater than that of ultraviolet light. As X-rays have greater frequency than ultraviolet rays, so they can cause photoelectric effect.
(iv) (b): \(\mathrm{K.E}_{\cdot 1}=h \mathrm{v}-\phi\)
\({K.E}_{\cdot 2}=n h v-\phi=n(h v-\phi)+(n-1) \phi\)
\({K.E.} 2=n \mathrm{KE}_{1}+(n-1) \phi \)
\(\text { K.E. }_{2}>n \mathrm{KE}_{1}\)
(v) (b): Stopping potential is the measurement of maximum kinetic energy of emitted photoelectrons and kinetic energy of emitted photoelectrons is linearly related with the frequency of incident light corresponding (i.e., corresponding to shortest wavelength, KE. is maximum). Stopping potential is independent of intensity. -
(i) (d): Power of light received by the cone \(=I\left(\pi R^{2}\right)\)
Let number of photons hitting the cone per second is n.
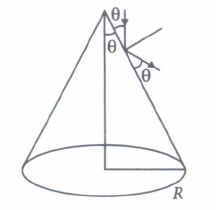
Then, \(n E=I \pi R^{2} \Rightarrow n=\pi R^{2} I / E\)
(ii) (b): Initial moment \(p_{i}=\frac{E}{c}\)
For a perfectly selecting surface
Final momentum \(p_{f}=\frac{-E}{c}\)
\(\Delta p=p_{f}-p_{i}=\frac{-E}{c}-\frac{E}{c}=\frac{-2 E}{c}\)
Hence a momentum \(\frac{2 E}{c}\) is transferred to the reflecting surface.
(iii) (a): According to the theory of relatively,
\(E=m c^{2}=m c . c=p c\)
\(\text { or } \quad E^{2}=p^{2} c^{2}\)
where p is the momentum of a photon.
(iv) (b): I = 1 kWm-2
As, 50% of light is reflected, thus e = 0.5
Radiation pressure \(P=\frac{(1+e) I}{c}\)
\(\therefore \quad P=\frac{(1+0.5) \times 1000}{3 \times 10^{8}}=5 \times 10^{-6} \mathrm{~Pa}\)
(v) (a) : \(\frac{P_{\mathrm{rad}}}{P_{0}}=\frac{5 \times 10^{-6}}{1 \times 10^{5}}=5 \times 10^{-11}\) -
(i) (c) :de Broglie wavelength, \(\lambda=\frac{h}{p}\)
where p is the momentum of the particle For electron \(\lambda_{e}=\frac{h}{p_{e}}\)
For proton \(\lambda_{e}=\frac{h}{p_{p}}\)
\(\text { As } \lambda_{e}=\lambda_{p} \Rightarrow p_{e}=p_{p}\) (Given)
or Momentum of electron = Momentum of proton
(ii) (a) : \(\text { As } \lambda-\frac{h}{\sqrt{2 m K}} \text { so } \lambda \sim \frac{1}{\sqrt{m}}\)
Out of the given particles m is least for electron, therefore electron has the largest value of de Broglie wavelength.
(iii) (a) : \(\text { As } \lambda=\frac{h}{p} \text { or } p=\frac{h}{\lambda} \text { or } p \propto \frac{1}{\lambda}\)
\(\therefore \quad \frac{P_{1}}{P_{2}}=\frac{\lambda_{2}}{\lambda_{1}}=\frac{\lambda}{\lambda}=1 \text { or } p_{1}=p_{2} \)
\(\text { Also } E=\frac{1}{2} \frac{p^{2}}{m}=\frac{1}{2 m} \frac{h^{2}}{\lambda^{2}} \quad\left(\because p=\frac{h}{\lambda}\right) \)
\((\text { or } \quad E \propto \frac{1}{m} \therefore \frac{E_{1}}{E_{2}}=\frac{m_{2}}{m_{1}}<1 \text { or } E_{1} )\)
(iv) (b): The de Broglie wavelength is given by
\(\lambda=\frac{h}{p}=\frac{h}{m v}\)
So if the velocity of the electron increases, the de -Broglie wavelength decreases.
(v) (d): \(\lambda=\frac{h}{p}\) when \(\lambda\) is same, P is also same. -
(i) (a): The existence of the frequency and the instantaneous emission of photo electrons support the quantum nature of light.
(ii) (b): For photoelectric emission, the incident light must have a certain minimum frequency, called threshold frequency.
(iii) (a): From Einstein's relation
\(e V_{s}=h v-W\)
As work function is a constant for a surface
\(e\left(V_{s_{2}}-V_{s_{1}}\right)=h\left(v_{2}-v_{1}\right)\)
\(V_{s_{2}}=V_{s_{1}}+\frac{h}{e}\left(v_{2}-v_{1}\right)\)
\(=0.19+1240\left(\frac{1}{190}-\frac{1}{550}\right)=4.47 \mathrm{~V}\)
(iv) (b): \(W=\frac{h c}{\lambda_{1}}-e V_{s_{1}}=\frac{1240}{550}-0.19=2.07 \mathrm{eV}\)
(v) (a): hve = W -
(i) (a): Particle nature of light was established by photoelectric effect.
(ii) (a): Photons move with velocity of light and have energy hv. Therefore, they also exert pressure.
(iii) (d): The rest mass of photon is zero.
(iv) (b): In a photon-particle collision, (such as photon electron collision), the total energy and total momentum are conserved. However, the number of photons may not be conserved in photon-particle collision. The photon may be absorbed or a new photon may be created.
(v) (d): Energy of n photons \(E=\frac{n h c}{\lambda}\)
Momentum gam. ed by the body, \(p=\frac{E}{c}=\frac{n h c}{\lambda c}=\frac{n h}{\lambda}\) -
(i) (c)
(ii) (b)
(iii) (a)
(iv) (a)
(v) (c): In discharge tube, collision between charged particles emitted from cathode and atoms of the gas results to colorless glow in the tube. -
(i) If electrode B is positive, then photoelectrons emitted from electrode A will accelerate towards B and will be absorbed. But, if potential of electrode B is decreased W.r.t. potential of A, i.e., electrode B is negative, then emitted photoelectrons will experience retardation and only that electron will be able to reach electrode B which has sufficient kinetic energy, and then only photoelectric current will become zero.
(ii)\(\lambda\)(nm) 589 552 330 285 \(v=\frac{c}{\lambda}\left(\times 10^{14}\right) \mathrm{Hz}\) 5.1 5.4 9.1 10.5 Vo(V) 0.246 0.367 1.870 2.463 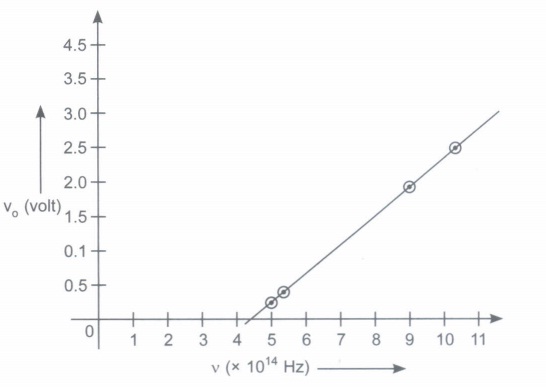
According to Einstein's equation
\(\mathrm{K}_{\max }=e \mathrm{~V}_{\mathrm{o}}=h \mathrm{v}-\phi_{\mathrm{o}}\)
\(\mathrm{V}_{\mathrm{o}}=\left(\frac{h}{e}\right) \mathrm{v}-\frac{\phi_{\mathrm{o}}}{e}\)
\(\therefore\) Slope of Vo vs v graph \(=\frac{h}{e}\)
\(\frac{2.463-0.246}{(10.5-5.1) \times 10^{14}}=\frac{h}{1.6 \times 10^{-19}}\)
\(h=\frac{2.217 \times 1.6 \times 10^{-19}}{5.4 \times 10^{14}}\)
= 0.657 x 10- 33
h = 6.6 x 10- 34 J S-1
\(\therefore\) from the graph
v0 = Threshold frequency
= 4.5 x 1014 Hz
\(\therefore\) Work function \(\phi_{\mathrm{o}}=h v_{\mathrm{o}}=6.6 \times 10^{-34} \times 4.5 \times 10^{14}\)
\(\phi_{\mathrm{o}}=2.97 \times 10^{-19} \mathrm{~J}\)






































