Class 12th Physics - Wave Optics Case Study Questions and Answers 2022 - 2023
By QB365 on 09 Sep, 2022
QB365 provides a detailed and simple solution for every Possible Case Study Questions in Class 12th Physics Subject - Wave Optics, CBSE. It will help Students to get more practice questions, Students can Practice these question papers in addition to score best marks.
QB365 - Question Bank Software
Wave Optics Case Study Questions With Answer Key
12th Standard CBSE
-
Reg.No. :
Physics
-
If double slit apparatus is immersed in a liquid of refractive index, I-l the wavelength of light reduces to \(\lambda\) and fringe width also reduces to \(\beta^{\prime}=\frac{\beta}{\mu} \text { . }\)
The given figure shows a double-slit experiment in which coherent monochromatic light of wavelength A from a distant source is incident upon the two slits, each of width w(w >> \(\lambda\)) and the interference pattern is viewed on a distant screen. A thin piece of glass of thickness t and refractive index n is placed between one of the slit and the screen, perpendicular to the light path.
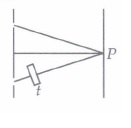
(i) In Young's double slit interference pattern, the fringe width(a) can be changed only by changing the wavelength of incident light (b) can be changed only by changing the separation between the two slits (c) can be changed either by changing the wavelength or by changing the separation between two sources (d) is a universal constant and hence cannot be changed (ii) If the width w of one of the slits is increased to 2w, the become the amplitude due to slit
(a) 1.5a (b) a/2 (c) 2a (d) no change (iii) In YDSE, let A and B be two slits. Films of thicknesses tA and tB and refractive indices mA and mB are placed in front of A and B, respectively. If \(\mu_{\mathrm{A}} t_{A}=\mu_{B} t_{B}\) then the central maxima will
(a) not shift (b) shift towards A (c) shift towards B (d) shift towards A if tB = tA and shift towards B if tB < tA (iv) In Young's double slit experiment, a third slit is made in between the double slits. Then
(a) fringes of unequal width are formed. (b) contrast between bright and dark fringes is reduced (c) intensity of fringes totally disappears (d) only bright light is observed on the screen (v) In Young's double slit experiment, if one of the slits is covered with a microscope cover slip, then
(a) fringe pattern disappears (b) the screen just gets illuminated (c) in the fringe pattern, the brightness of the bright fringes will decreases and the dark fringes will become more dark (d) bright fringes will be more bright and dark fringes will become more dark. (a) -
Distance between two successive bright or dark fringes is called fringe width.
\(\beta=Y_{n+1}-Y_{n}=\frac{(n+1) \lambda D}{d}-\frac{n \lambda D}{d}=\frac{\lambda D}{d}\)
Fringe width is independent of the order of the maxima. If whole apparatus is immersed in liquid of refractive index \(\mu\) then \(\beta=\frac{\lambda D}{\mu d}\) (fringe width decreases). Angular fringe width (\(\theta\)) is the angular separation between two consecutive maxima or minima \(\theta=\frac{\beta}{D}=\frac{\lambda}{d}\)
In the arrangement shown in figure, slit S3 and S4 are having a variable separation Z. Point 0 on the screen is at the common perpendicular bisector of S1S2 and S3S4.
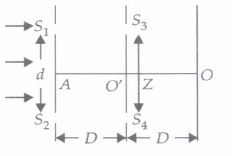
(i) The maximum number of possible interference maxima for slit separation equal to twice the wavelength in Young's double-slit experiment, is(a) infinite (b) five (c) three (d) zero (ii) In Young's double - slit experiment if yellow light is replaced by blue light, the interference fringes become
(a) wider (b) brighter (c) narrower (d) darker (iii) In Young's double slit experiment, if the separation between the slits is halved and the distance between the slits and the screen is doubled, then the fringe width compared to the unchanged one will be
(a) Unchanged (b) Halved (c) Doubled (d) Quadrupled (iv) When the complete Young's double slit experiment is immersed in water, the fringes
(a) remain unaltered (b) become wider (c) become narrower (d) disappear (v) In a two slit experiment with white light, a white fringe is observed on a screen kept behind the slits. When the screen is moved away by 0.05 m, this white fringe
(a) does not move at all (b) gets displaced from its earlier position (c) becomes coloured (d) disappears (a) -
When light from a monochromatic source is incident on a single narrow slit, it gets diffracted and a pattern of alternate bright and dark fringes is obtained on screen, called "Diffraction Pattern" of single slit. In diffraction pattern of single slit, it is found that
(I) Central bright fringe is ·of maximum intensity and the intensity of any secondary bright fringe decreases with increase in its order.
(II) Central bright fringe is twice as wide as any other secondary bright or dark fringe .
(i) A single slit of width 0.1 mm is illuminated by a parallel beam of light of wavelength 6000 A and diffraction bands are observed on a screen 0.5 m from the slit. The distance of the third dark band from the central bright band is(a) 3 mm (b) 1.5 mm (c) 9 mm (d) 4.5 mm (ii) In Fraunhofer diffraction pattern, slit width is 0.2 mm and screen is at 2 m away from the lens. If wavelength of light used is 5000 \(\lambda\) then the distance between the first minimum on either side the central maximum is
(a) 10-1 m (b) 10-2 m (c) 2 x 10-2 m (d) 2 x 10-1 m (iii) Light of wavelength 600 nm is incident normally on a slit of width 0.2 mm. The angular width of central maxima in the diffraction pattern is (measured from minimum to minimum)
(a) 6 x 10-3 rad (b) 4 x 10-3 rad (c) 2.4 x 10-3 rad (d) 4.5 x 10-3 rad (iv) A diffraction pattern is obtained by using a beam of red light. What will happen, if the red light is replaced by the blue light?
(a) bands disappear (b) bands become broader and farther apart (c) no change will take place (d) diffraction bands become narrower and crowded together. (v) To observe diffraction, the size of the obstacle
(a) should be A/2, where A is the wavelength. (b) should be of the order of wavelength. (c) has no relation to wavelength. (d) should be much larger than the wavelength. (a) -
In Young's double slit experiment, the width of the central bright fringe is equal to the distance between the first dark fringes on the two sides of the central bright fringe.
In given figure below a screen is placed normal to the line joining the two point coherent source SI and S2' The interference pattern consists of concentric circles.
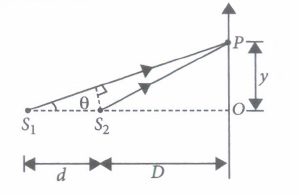
(i) The optical path difference at P is\((a) d\left[1+\frac{y^{2}}{2 D}\right]\) \((b) d\left[1+\frac{2 D}{y^{2}}\right]\) \((c) d\left[1-\frac{y^{2}}{2 D^{2}}\right]\) \((d) d\left[2 D-\frac{1}{y^{2}}\right]\) (ii) Find the radius of the nth bright fringe.
\((a) D \sqrt{1\left(1-\frac{n \lambda}{d}\right)}\) \((b) D \sqrt{2\left(1-\frac{n \lambda}{d}\right)}\) \((c) 2 D \sqrt{2\left(1-\frac{n \lambda}{d}\right)}\) \((d) D \sqrt{2\left(1-\frac{n \lambda}{2 d}\right)}\) (iii) If d = 0.5 mm, \(\lambda\)= 5000 \(\dot A \)and D = 100 em, find the value of n for the closest second bright fringe
(a) 888 (b) 830 (c) 914 (d) 998 (iv) The coherence of two light sources means that the light waves emitted have
(a) same frequency (b) same intensity (c) constant phase difference (d) same velocity. (v) The phenomenon of interference is shown by
(a) longitudinal mechanical waves only (b) transverse mechanical waves only (c) electromagnetic waves only (d) all of these (a) -
A narrow tube is bent in the form of a circle of radius R, as shown in figure. Two small holes S and D are made in the tube at the positions at right angle to each other. A source placed at S generates a wave of intensity Io which is equally divided into two parts: one part travels along the longer path, while the other travels along the shorter path. Both the waves meet at point D where a detector is placed.
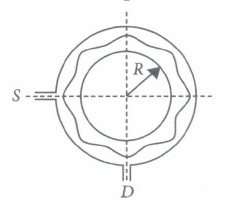
(i) If a maxima is formed at a detector, then the magnitude of wavelength \(\lambda\) of the wave produced is given by\((a) \pi R\) \((b) \frac{\pi R}{2}\) \((c) \frac{\pi R}{4}\) (d) all of these (ii) If the intensity ratio of two coherent sources used in Young's double slit experiment is 49 : 1, then the ratio between the maximum and minimum intensities in the interference pattern is
(a) 1: 9 (b) 9: 16 (c) 25: 16 (d) 16: 9 (iii) The maximum intensity produced at D is given by
(a) 4I0 (b) 2I0 (c) I0 (d) 3I0 (iv) In a Young's double slit experiment, the intensity at a point where the path difference is \(\lambda\)/6 (\(\lambda\) - wavelength of the light) is I. If I0 denotes the maximum intensity, then I/I0 is equal to
\((a) \frac{1}{2}\) \((b) \frac{\sqrt{3}}{2}\) \((c) \frac{1}{\sqrt{2}}\) \((d) \frac{3}{4}\) (v) Two identical light waves, propagating in the same direction, have a phase difference d. After they superpose the intensity of the resulting wave will be proportional to
\((a) \cos \delta\) \((b) \cos (\delta / 2)\) \((c) \cos ^{2}(\delta / 2)\) \((d) \cos ^{2} \delta\) (a) -
Consider the situation shown in figure. The two slits S1 and S2 placed symmetrically around the central line are illuminated by monochromatic light of wavelength \(\lambda\). The separation between the slits is d. The light transmitted. by the slits falls on a screen S0 place at a distance D from the slits. The slits S3 is at the central line and the slit S4 is at a distance from S3. Another screen Sc is placed a further distance D away from Sc.

(i) Find the path difference if \(z=\frac{\lambda D}{2 d}\)\((a) \lambda\) \((b) \lambda / 2\) \((c) 3 / 2 \lambda\) \((d) 2 \lambda\) (ii) Find the ratio of the maximum to minimum intensity observed on \(S_{c} \text { if } z=\frac{\lambda D}{d}\)
(a) 4 (b) 2 (c) \(\infty\) (d) 1 (iii) Two coherent point sources S1 and S2 are separated by a small distance d as shown in figure. The fringes obtained on the screen will be
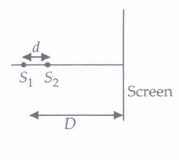
(a) Concentric Circles (b) points (c) Straight lines (d) semi-circles (iv) In the case of light waves from two coherent sources S1 and S2. there will be constructive interference at an arbitrary point P, if the path difference S1P - S2P is
\(\text { (a) }\left(n+\frac{1}{2}\right) \lambda \) \( \text { (b) } n \lambda\) \( \text { (c) }\left(n-\frac{1}{2}\right) \lambda\) \( \text { (d) } \frac{\lambda}{2}\) (v) Two monochromatic light waves of amplitudes 3A and 2A interfering at a point have a phase difference of 60°. The intensity at that point will be proportional to
(a) 5A2 (b) 13A2 (c) 7A2 (d) 19A2 (a) -
Wavefront is a locus of points which vibratic in same phase. A ray of light is perpendicular to the wavefront. According to Huygens principle, each point of the wavefront is the source of a secondary disturbance and the wavelets connecting from these points spread out in all directions with the speed of wave. The figure shows a surface XY separating two transparent media, medium-1 and medium-2. The lines ab and cd represent wavefronts of a light wave travelling in medium- 1 and incident on XY. The lines ef and gh represent wavefronts of the light wave in medium -2 after refraction.
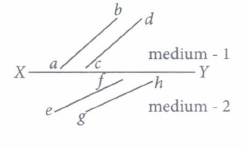
(i) Light travels as a(a) parallel beam in each medium (b) convergent beam in each medium (c) divergent beam in each medium (d) divergent beam in one medium and convergent beam in the other medium. (ii) The phases of the light wave at c, d, e and f are \(\phi_{c}, \phi_{d}, \phi_{e}\) and \( \phi_{f}\) respectively. It is given that \(\phi_{c} \neq \phi_{f}\)
\(\text { (a) } \phi_{c} \text { cannot be equal to } \phi_{d}\) \(\text { (b) } \phi_{d} \text { can be equal to } \phi_{e}\) \(\text { (c) }\left(\phi_{d}-\phi_{f}\right) \text { is equal to }\left(\phi_{c}-\phi_{e}\right)\) \(\text { (d) }\left(\phi_{d}-\phi_{c}\right) \text { is not equal to }\left(\phi_{f}-\phi_{e}\right)\) (iii) Wavefront is the locus of all points, where the particles of the medium vibrate with the same
(a) phase (b) amplitude (c) frequency (d) period (iv) A point source that emits waves uniformly in all directions, produces wavefronts that are
(a) spherical (b) elliptical (c) cylindrical (d) planar (v) What are the types of wavefronts ?
(a) Spherical (b) Cylindrical (c) Plane (d) All of these (a) -
Huygen's principle is the basis of wave theory of light. Each point on a wavefront acts as a fresh source of new disturbance, called secondary waves or wavelets. The secondary wavelets spread out in all directions with the speed light in the given medium.An initially parallel cylindrical beam travels in a medium of refractive index \(\mu(I)=\mu_{0}+\mu_{2} I\), where \(\mu_{0} \text { and } \mu_{2}\)are positive constants and I is the intensity of the light beam. The intensity of the beam is decreasing with increasing radius.
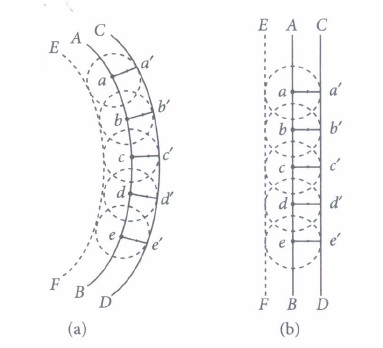
(i) The initial shape of the wavefront of the beam is(a) planar (b) convex (c) concave (d) convex near the axis and concave near the periphery (ii) According to Huygens Principle, the surface of constant phase is
(a) called an optical ray (b) called a wave (c) called a wavefront (d) always linear in shape (iii) As the beam enters the medium, it will
(a) travel as a cylindrical beam (b) diverge (c) converge (d) diverge near tile axis and converge near the periphery. (iv) Two plane wavefronts of ligbt, one incident on a thin convex lens and another on the refracting face of a thin prism. After refraction at them, the emerging wavefronts respectively become
(a) plane wavefront and plane wavefront (b) plane wavefront and spherical wavefront (c) spherical wavefront and plane wavefront (d) spherical wavefront and spherical wavefront (v) Which of the following phenomena support the wave theory of light?
1. Scattering
2. Interference
3. Diffraction
4. Velocity of light in a denser medium is less than the velocity of light in the rarer medium(a) 1,2,3 (b) 1,2,4 (c) 2,3,4 (d) 1,3,4 (a) -
The phenomenon of bending of light around the sharp corners and the spreading of light within the geometrical shadow of the opaque obstacles is called diffraction of light. The light thus deviates from its linear path. The deviation becomes much more pronounced, when the dimensions of the aperture or the obstacle are comparable to the wavelength of light.
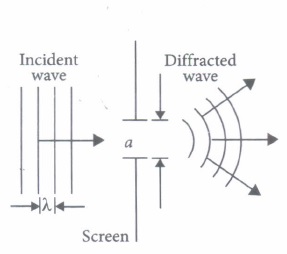
(i) Light seems to propagate in rectilinear path because(a) its spread is very large (b) its wavelength is very small (c) reflected from the upper surface of atmosphere (c) it is not absorbed by atmosphere (ii) In diffraction from a single slit the angular width of the central maxima does not depends on
(a) \(\lambda\) of light used (b) width of slit (c) distance of slits from the screen (d) ratio of \(\lambda\) and slit width (iii) For a diffraction from a single slit, the intensity of the central point is
(a) infinite (b) finite and same magnitude as the surrounding maxima (c) finite but much larger than the surrounding maxima (d) finite and substantially smaller than the surrounding maxima (iv) .Resolving power of telescope increases when
(a) wavelength of light decreases (b) wavelength of light increases (c) focal length of eye-piece increases (d) focal length of eye-piece decreases (v) In a single diffraction pattern observed on a screen placed at D metre distance from the slit of width d metre, the ratio of the width of the ce,ntral maxima to the width of other secondary maxima is
(a) 2: 1 (b) 1: 2 (c) 1: 1 (d) 3: 1 (a) -
Interference is based on the superposition principle. According to this principle, at a particular point in the medium, the resultant displacement produced by a number of waves is the vector sum of the displacements produced by each of the waves. If two sodium lamps illuminate two pinholes S1 and S2. The intensities will add up and no interference fringes will be observed on the screen. Here the source undergoes abrupt phase change in times of the order of 10-10 seconds.
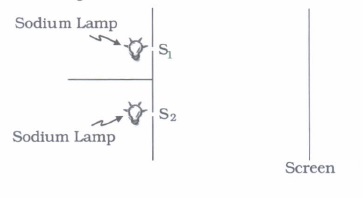
(i) Two coherent sources of intensity 10 W/m2 and 25 W/m2 interfere to form fringes. Find the ratio of maximum intensity to minimum intensity(a) 15.54 (b) 16.78 (c) 19.72 (d) 18.39 (ii) Which of the following does not show interference?
(a) Soap bubble (b) Excessively thin film (c) A thick film (d) Wedge shaped film (iii) In a Young's double-slit experiment, the slit separation is doubled. To maintain the same fringe spacing on the screen, the screen-to-slit distance D must be changed to
(a) 2D (b) 4D (c) D/2 (d) D/4 (iv) The maximum number of possible interference maxima for slit separation equal to twice the wavelength in Young's double-slit experiment, is
(a) infinite (b) five (c) three (d) zero (v) The resultant amplitude of a vibrating particle by the superposition of the two waves \(y_{1}=a \sin \left[\omega t+\frac{\pi}{3}\right] \text { and } y_{2}=a \sin \omega t \text { is }\)
(a) a (b)\(\sqrt{2}\) a (c) 2a (d) \(\sqrt{3}\) a (a) -
Figure shows a surface XY separating two transparent media, medium 1 and medium 2. Lines ab and cd represent wavefronts of a light wave traveling in a medium 1 and incident on XY. Lines ef and gh represent wavefront of the light wave in medium 2 after refraction.
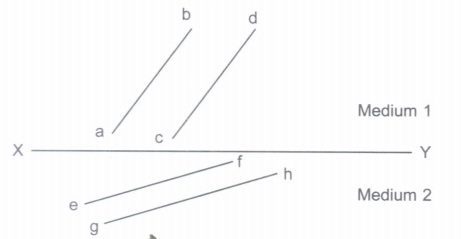
(i) How does light travels in each medium?
(il) The phases of the light waves at c, d, e and f are \(\phi_{c}, \phi_{d}, \phi_{e} \text { and } \phi_{f}\) respectively. It is given that \(\phi_{c} \neq \phi_{f}\). Then \(\left(\phi_{d}-\phi_{f}\right)\) is equal to ________
(iii) Is speed of light in two media same?
If v1 and v 2 are speed of light in two media 1 and 2 respectively, then write the relationship between v1 and v2.
(iv) Why there is no change in frequency? Show mathematically.(a) -
Huygens Wave Theory of Light
1. According to wave theory, light from a source is propagated in the form of longitudinal waves with uniform velocity in a homogeneous medium.
2. To explain the propagation of waves through vacuum, Huygens assumed existance of a hypothetical medium called luminiferous ether. According to Huygens, ether particles are present and possess properties such as inertia, zero density and perfect transparency.
3. On the basis of Huygens wave theory, various colours of light are due to different wavelengths of the light of the waves.
(i) Write two merits and two demerits of Huygens wave theory of light.
(ii) Write Huygen's postulates to explain wave theory of light.
(iii) What are primary source and secondary source of light considered in wave theory?(a) -
While comparing the interference pattern with that seen for a coherently illuminated single slit (usually called single slit diffraction pattern), the interference pattern has a number of equally spaced bright and dark bands. The diffraction pattern has a central bright maximum which is twice as wide as the other maxima. The intensity falls as we go to successive maxima away from the centre, on either side. Now answer the following questions:
(i) Why interference fringes are equispaced whereas that of diffraction are not?
(ii) Why intensity falls as we go to successive maxima away from central bright maximum?
(iii) For a single slit of width a, the first null point of the interference pattern occurs at an angle of \(\lambda\)/a. At the same angle of \(\lambda\)/a, we get a maximum (not a null) for two narrow slits separated by a distance a. Explain why?(a) -
"According to Richard Feynman, no one has ever been able to distinguish between interference and diffraction satisfactorily. Roughly speaking if the number of sources are few, say two interfering sources then the result is usually interference, but if there is a large number of them, it seems that the word diffraction is more often used". Now explain the following:
(i) "In the double-slit experiment, the pattern on the screen is due to superposition of single slit diffraction from each slit." Justify this statement.
(il) In a double slit experiment, the wavelength \(\lambda\) of the light source is 400 nm, the slit separation is 20\(\mu\)m, and the slit width a is 4\(\mu\)m. Consider the interference of the light from the two slits and also diffraction of the light through each slit
(a) Determine how many bright fringes are within the central peak of the diffraction envelope?
(b) How many bright fringes are within either of the first side peak of the diffraction envelope?(a)
Case Study
*****************************************
Answers
Wave Optics Case Study Questions With Answer Key Answer Keys
-
(i) (c): In Young's double slit experiment, the fringe width is \(\beta=\frac{D \lambda}{d}\) where Dis the distance of the slits from the screen, d is the separation of the slits and \(\lambda\), the wavelength. Therefore the fringe width \(\beta\) can be changed either by changing the separation between the sources or the distance of the screen from the sources.
(ii) (c): As the width of one of the slits is increased to 2w, the amplitude due to slit become 2a.
(iii) (d): \(\Delta x=\left(\mu_{A}-1\right) t_{A}-\left(\mu_{B}-1\right) t_{B}\)
\(=\mu_{A} t_{A}-\mu_{B} t_{B}-t_{A}+t_{B}=t_{B}-t_{A}\)
If \(\Delta x\)> 0, then fringe pattern will shift upward.
If \(\Delta x\)< 0, then fringe pattern will shift downwards.
(iv) (b): Contrast between the bright and dark fringes will be reduced.
(v) (a): Since, one of the slit is covered, interference will not occur and fringe pattern will disappear.
-
(i) (b): The condition for possible interference maxima on the screen is, dsin\(\theta\) = nA
where d is slit separation and Ais the wavelength.
As d = 2\(\lambda\) (given) \(\therefore\) 2\(\lambda\)sin\(\theta\)= n\(\lambda\) or 2sin\(\theta\) = n
For number of interference maxima to be maximum,
sin\(\theta\) = 1 \(\therefore\) n = 2
The intprference maxima will be forgied when
n = 0, ± 1, ± 2
Hence the maximum number of possible maxima is 5.
(ii) (c): Fringe width, \(\beta=\frac{\lambda D}{d}\)
\(\therefore\) If we replace yellow light with blue light, i.e., longer wavelength with shorter one, therefore the fringe width decreases.
(iii) (d): \(d^{\prime}=\frac{d}{2} \text { and } D^{\prime}=2 D\)
Fringe width, \(\beta=\frac{\lambda D}{d}\)
New fringe width \(\beta^{\prime}=\lambda\left(\frac{2 D}{d / 2}\right)=4 \beta\)
(iv) (c): When Young's double slit experiment is repeated in water, instead of air \(\lambda^{\prime}=\frac{\lambda}{\mu}\) i.e., wavelength decreases.\(\beta=\frac{\lambda^{\prime} D}{d}\) i.e..,fringe width decreases.
\(\therefore\) The fringe become narrower.
(v) (a): Using white light, we get white fringe at the centre i.e., white fringe is the central maximum. When the screen is moved, its position is not changed. -
(i) (c) : Here \(d=0.1 \mathrm{~mm}, \lambda=6000 \dot A, D=0.5 \mathrm{~m}\)
For third dark band \(d \sin \theta=3 \lambda ; \sin \theta=\frac{3 \lambda}{d}=\frac{y}{D}\)
\(y=\frac{3 D \lambda}{d}=\frac{3 \times 0.5 \times 6 \times 10^{-7}}{0.1 \times 10^{-3}}=9 \times 10^{-3} \mathrm{~m}=9 \mathrm{mn}\)
(ii) (b): Given \(d=0.2 \mathrm{~mm}=0.2 \times 10^{-3} \mathrm{~m}, D=2 \mathrm{~m}\)
\(\lambda=5000 \dot A=5 \times 10^{-7} \mathrm{~m}\)
The distance between the first minimum on other side of the central maximum
\(x=\frac{2 \lambda D}{d}=\frac{2 \times 5 \times 10^{-7} \times 2}{0.2 \times 10^{-3}} \Rightarrow x=10^{-2} \mathrm{~m}\)
(iii) (a): Here \(\lambda=600 \mathrm{nm}=6 \times 10^{-7} \mathrm{~m}\)
\(a=0.2 \mathrm{~mm}=2 \times 10^{-4} \mathrm{~m}, \theta=?\)
Angular width of central maxima
\(\theta=\frac{2 \lambda}{a}=\frac{2 \times 6 \times 10^{-7}}{2 \times 10^{-4}}=6 \times 10^{-3} \mathrm{rad}\)
(iv) (d) : When red light is replaced by blue light (\(\lambda\)B < \(\lambda\)R) the diffraction pattern bands becomes narrow and crowded together.
(v) (b) : To observe diffraction, the size of the obstacle should be of the order of wavelength. -
(i) (c):The optical path difference at P is
\(\Delta x=S_{1} P-S_{2} P=d \cos \theta\)
\(\because \quad \cos \theta=1-\frac{\theta^{2}}{2} \text { for small } \theta\)
\(\therefore \quad \Delta x=d\left(1-\frac{\theta^{2}}{2}\right)=d\left[1-\frac{y^{2}}{2 D^{2}}\right], \text { where } D+d=D\)
(ii) (b) : \(\text { For } n^{\text {th }} \text { maxima, }\)
\(\Rightarrow \Delta x=n \lambda\)
\(d\left[1-\frac{y^{2}}{2 D^{2}}\right]=n \lambda\)
Y = radius of the nth bright ring
\(=D \sqrt{2\left(1-\frac{n \lambda}{d}\right)}\)
(iii) (d): At the central maxima, \(\theta\)= 0.
\(\Delta x=d=n \lambda \)
\(\Rightarrow n=\frac{d}{\lambda}=\frac{0.5}{0.5 \times 10^{-3}}=1000\)
Hence, for the closet second bright fringe, n = 998.
(iv) (c): Light waves from two coherent sources must have a constant phase difference.
(v) (d): Interference is shown by transverse as well as mechanical waves. -
(i) (d): Path difference produced is
\(\Delta x=\frac{3}{2} \pi R-\frac{\pi}{2} R=\pi R\)
For maxima \(\Delta x=n \lambda\)
\(\begin{array}{l} \therefore \quad n \lambda=\pi R \\ \Rightarrow \lambda=\frac{\pi R}{n}, n=1,2,3, \ldots . \end{array}\)
Thus, the possible values of \(\lambda \text { are } \pi R, \frac{\pi R}{2}, \frac{\pi R}{3}, \ldots\)
(ii) (d)
(iii) (b): Maximum intensity \(I_{\max }=\left(\sqrt{I_{1}}+\sqrt{I_{2}}\right)^{2}\)
\(\text { Here, } I_{1}=I_{2}=\frac{I_{0}}{2} \text { (given) }\)
\(\therefore \quad I_{\max }=\left(\sqrt{\frac{I_{0}}{2}}+\sqrt{\frac{I_{0}}{2}}\right)^{2}=2 I_{0}\)
(iv) (d): Phase difference \(\phi=\frac{2 \pi}{\lambda}\) x path diffrerence
\(\phi=\frac{2 \pi}{\lambda} \times \frac{\lambda}{6}=\frac{\pi}{3}=60^{\circ} \text { As } I=I_{\max } \cos ^{2} \frac{\phi}{2}\)
\(\therefore \quad I=I_{0} \cos ^{2} \frac{60^{\circ}}{2}=I_{0} \times\left(\frac{\sqrt{3}}{2}\right)^{2}=\frac{3}{4} I_{0} \Rightarrow \frac{I}{I_{0}}=\frac{3}{4}\)
(v) (c): HereA2 = \(a_{1}^{2}+a_{2}^{2}+2 a_{1} a_{2} \cos \delta \because a_{1}=a_{2}=a\)
\(\therefore A^{2}=2 a^{2}(1+\cos \delta)=2 a^{2}\left(1+2 \cos ^{2} \frac{\delta}{2}-1\right)\)
\(\text { or } A^{2} \propto \cos ^{2} \frac{\delta}{2}\)
\(\text { Now } I \propto A^{2} \quad \therefore I \propto A^{2} \propto \cos ^{2} \frac{\delta}{2} \Rightarrow I \propto \cos ^{2} \frac{\delta}{2}\) -
(i) (b): \(\text { As } z=\frac{\lambda D}{2 d}\)
\(\text { At } S_{4}: \frac{\Delta x}{d}=\frac{z}{D}\)
\(\Rightarrow \Delta x=\frac{\lambda D}{2 d} \frac{d}{d}=\frac{\lambda}{2}\)
(ii) (c): \(z=\frac{\lambda D}{d}\)
\(\Delta x \text { at } S_{4}: \Delta x=\frac{\lambda D}{d} \frac{d}{d}=\lambda\)
Hence, maxima at S4 as well as S3'
Resultant intensity at S4 I = 4I0
\(\therefore \quad \frac{I_{\max }}{I_{\min }}=\frac{\left[\left(4 I_{0}\right)^{1 / 2}+4\left(4 I_{0}\right)^{1 / 2}\right]^{2}}{\left[\left(4 I_{0}\right)^{1 / 2}-\left(4 I_{0}\right)^{1 / 2}\right]^{2}}=\infty\)
(iii) (a): When the screen is placed perpendicular to the line joining the 'sources, the fringes will be concentric circles.
(iv) (b): Constructive interference occurs when the path difference (S1P - S2P) is an integral multiple of \(\lambda\).or S1P - S2P = n\(\lambda\), where n = 0,1,2,3, .....
(v) (d): Here, A1 = 3A, A2 = 2A and \(\varphi\)= 60° The resultant amplitude at a point is
\(R =\sqrt{A_{1}^{2}+A_{2}^{2}+2 A_{1} A_{2} \cos \phi} \)
\(=\sqrt{(3 A)^{2}+(2 A)^{2}+2 \times 3 A \times 2 A \times \cos 60^{\circ}} \)
\(=\sqrt{9 A^{2}+4 A^{2}+6 A^{2}}=A \sqrt{19}\)
As, Intensity \(\infty\) (Amplituder)2 Therefore, intensity at the same point is
\(I \propto 19 A^{2}\) -
(i) (a): Since the path difference between two waveform is equal, light traves as parallel beam in each medium.
(ii) (c): Since all points on the wavefront are in the same phase,
\(\phi_{d}=\phi_{c} \text { and } \phi_{f}=\phi_{e} \)
\(\therefore \phi_{d}-\phi_{f}=\phi_{c}-\phi_{e^{-}}\)
(iii) (a): Wavefront is the locus of all points, where the particles of the medium vibrate with the same phase
(iv) (a)
(v) (d) -
(i) (a): As the beam is initially parallel, the shape of wavefront is planar.
(ii) (c): According to Huygens Principle, the surface of constant phase is called a wavefront.
(iii) (c)
(iv) (c): After refraction, the emerging wavefronts respectively become spherical. wavefront and plane wavefront as shown in figures (a) and (b).
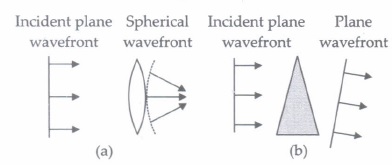
(v) (c) -
(i) (b): The wavelength of visible light is very small, that is hardly shows diffraction, so it seems to propagate in rectilinear path,
(ii) (c): Angular width of central maxima, 2\(\theta\) = 2\(\lambda\)/e. Thus, \(\theta\) does not depend on screen i.e., distance between the slit and the screen.
(iii) (c) : The intensity distribution of single slit diffraction pattern is shown in the figure. From the graph it is dear that the intensity of the central point is finite but much larger than the surrounding maxima.
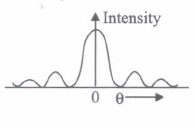
(iv) (a): Resolving power of telescope \(=\frac{a}{1.22 \lambda}\)
\(\therefore\) It increases when wavelength of light decreases and/or objective lens of greater diameter is used.
(v) (a): Width of central maxima = 2\(\lambda\) DIe
width of other secondary maxima = \(\lambda\)DI e
\(\therefore\)Width of central maxima: width of other secondary maxima
= 2 : 1 -
(i) (c) : Given \(I_{1}=10 \mathrm{~W} / \mathrm{m}^{2} \text { and } I_{2}=25 \mathrm{~W} / \mathrm{m}^{2}\)
\(\frac{I_{1}}{I_{2}}=\frac{a_{1}^{2}}{a_{2}^{2}}=\frac{10}{25} \Rightarrow \frac{a_{1}}{a_{2}}=\frac{3.16}{5} \text { or } a_{1}=\frac{3.16}{5} a_{2}=0.6324 a_{2}\)
\(\frac{I_{\max }}{I_{\min }}=\frac{\left(a_{1}+a_{2}\right)^{2}}{\left(a_{1}-a_{2}\right)^{2}}=\frac{\left[0.6324 a_{2}+a_{2}\right]^{2}}{\left[0.6324 a_{2}-a_{2}\right]^{2}}=19.724\)
(ii) (b): In an excessively thin film, the thickness of the film is negligible. Thus the path difference between the reflected rays becomes \(\lambda\)/2 which produces a minima.
(iii) (a): Since, \(\beta=\frac{\lambda D}{d} \text { for } d=2 d\)
\(\beta^{\prime}=\frac{\lambda D^{\prime}}{2 d}=\beta(\text { Gives })\)
\(\therefore \quad D_{1}=2 D\)
(iv) (b): The condition for possible interference maxima on the screen is, dsin \(\theta\) = n\(\lambda\)
where d is slit separation and Ais the wavelength.
\(\text { As } d=2 \lambda \text { (given) } \quad \therefore 2 \lambda \sin \theta=n \lambda \text { or } 2 \sin \theta=n\)
For number of interference maxima to be maximum,sin\(\theta\) = 1 :. n = 2
The interference maxima will be formed when n = 0, ± 1, ± 2
Hence the maximum number of possible maxima is 5.
(v) (d): \(y_{1}=a \sin \left(\omega t+\frac{\pi}{3}\right) \text { and } y_{2}=a \sin \omega t\)
\(A=\sqrt{a_{1}^{2}+a_{2}^{2}+2 a_{1} a_{2} \cos \phi}, \text { where } \phi=\frac{\pi}{3}\)
\(=\sqrt{a^{2}+a^{2}+2 a a \cos \frac{\pi}{3}}=\sqrt{3} a\) -
(i) Light travels as a parallel beam in each medium, as wavefronts are perpendicular to a beam of light, therefore wavefronts are plane parallel wavefronts in each media.
(ii) All points on a wavefront are at the same phase.
\(\phi_{d}=\phi_{c} \text { and } \phi_{f}=\phi_{e}\)
\(\therefore \phi_{d}-\phi_{f}=\phi_{c}-\phi_{e}\)
(iii) In medium 2, wavefront bends away from the normal after refraction. Therefore, ray of light which is perpendicular to wavefront bends towards the normal in medium 2 during refraction. So, medium 2 is denser or its speed in medium I is more or v1 > v 2 . So, the speed of light in two media is not same.
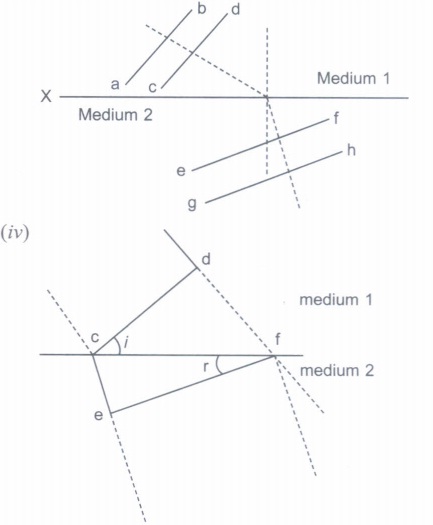
If part of wavefront reach from d to f with velocity speed v1, during this time another part will travel from c to e with speed v 2 .
If df = \(\lambda\)1 then ce = \(\lambda\)2 in medium 2
df = v1 x t ........(i)
ce = v 2 x t ...........(ii)
v1 and v2 are speeds in media 1 and 2 respectively.
then Dividing eq. (i) by eq. (ii) is \(\frac{v_{1} t}{v_{2} t}=\frac{\lambda_{1}}{\lambda_{2}}\) or \(\frac{v_{1}}{\lambda_{1}}=\frac{v_{2}}{\lambda_{2}}\) or v1 = v2 here v1, v2 are frequenecies in medium 1 and 2 respectively. -
(i) Merits of Huygens Wave theory of light:
(a) Wave theory correctly predicted that velocity of light in an optically denser medium is less than that in the rarer medium which is in agreement with the experimental results.
(b) On the basis of wave theory phenomenon of reflection, refraction, interference, diffraction, polarization of light could be explained.
Demiritssof Huygens wave theory of light
(a) Huygens wave theory assumes the existence of luminiferous ether. However,experimentally it couldn't be proved.
(b) This theory couldn't explain rectilinear propagation of light.
(ii) (1) Each pointon a given primary wavefront acts as a source of secondary wavelets, sending out disturbances (waves) in all directions in a similar manner as the original source of light does.
(2) The new position of the wavefront at any instant (secondary wavefront) is given by the forward envelope to the secondary wavelets at that instant.
Huygens' construction
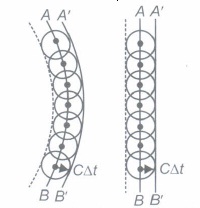
Using this principle the laws of reflection and refraction can be verified.
(iii) Primary source of light: It is a real source of light. It generates light itself and sends primary wavefronts in all directions.
Secondary source of light: It is a fictitious source of light presents on the wavefront and sends out secondary waves only in forward direction. -
(i) By the principle of interference, condition for constructive interference is the path difference = xn d/D = n\(\lambda\) here n = 0, 1,2 ... indicate the order of bright fringes. Therefore position of nth bright is given by
\(x_{n}=\frac{n \lambda \mathrm{D}}{d}\) and the dark fringe width
\(\beta=\frac{(n+1) \lambda D}{d}-\frac{n \lambda D}{d}=\frac{\lambda D}{d}\) ..........(i)
Similarly, condition for destructive inetreference is the path difference
\(=\frac{x_{n}^{\prime} d}{\mathrm{D}}=(2 n-1) \frac{\lambda}{2}\) therefore the position of nth dark fringe is given by \(x_{n}^{\prime}=(2 n-1) \frac{\lambda \mathrm{D}}{2 d}\) here n = 1, 2, 3 ... shows the order of dark fringes, and the bright fringe width
\(\beta=\frac{[2(n+1)-1] \lambda D}{2 d}-\frac{(2 n-1) \lambda D}{2 d}=\frac{\lambda D}{d} \) ..........(ii)
From eqs (i) and (ii) we see that width of bright and dark fringes are equal.
Let, A and a be the wavelength and slit width of the diffracting system respectively. Let O be the position of the central maximum.
s.png)
Condition for the first minimum is given by
\(a\sin { \theta } =m\lambda \) ...(i)
Let \(\theta\) be the angle of diffraction.
As, diffraction angle is small
\(\therefore\) \(\sin { \theta } \approx \theta \)
For first diffraction minimum,
\(\theta ={ \theta }_{ 1 }\)
For the first minimum, take m = I
\(a{ \theta }_{ 1 }=\lambda \quad \Rightarrow { \theta }_{ 1 }=\frac { \lambda }{ a } \)
Now, angular width, \(AB={ \theta }_{ 1 }\)
Angular width, \(BC={ \theta }_{ 1 }\)
Angular width, \(AC=2{ \theta }_{ 1 }\)
(ii) The maxima become weaker and weaker with increasing n...This is because the effective part of the wavefront, contributing to the maxima, becomes smaller and smaller, with increasing n.
(iii) In case of a single slit of width a, the wavelets from two halves of slit produce a minimum as the corresponding wavelets have a path difference of \(\frac{\lambda}{2}\).
In the second case, the overlapping of the wavefronts from the two slits produce first maximum because they meet with a path difference of \(\lambda\). -
(i) n the double-slit experiment, the pattern on the screen is actually a superposition of single-slit diffraction from each slit or hole and the double-slit interference pattern as shown in the given figure. It shows a broader diffraction peak in which there appear several fringes of smaller width due to double-slit interference. The number of interference fringes occuring in the broad diffraction peak depends on the ratio d/a, which is the ratio of the distance between the two slits to the width of a slit. In the limit of a becoming very small, the diffraction pattern will become flat and we will observe the two slit interference pattern.
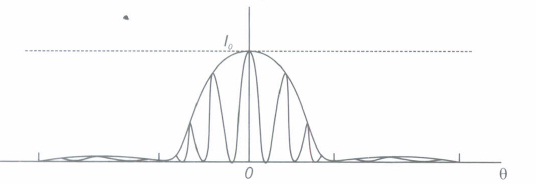
(ii) (a) \(\lambda\)Given = 400 nm
= 4 x 10- 7 m,
d = 20 \(\mu\)m = 2 x 10- 5 m,
a = 4\(\mu\)m = 4 x 10-6 m
If n = no. of bright fringes within central peak of diffraction envelope
Then \(\frac{2 \lambda \mathrm{D}}{a}=n \lambda \frac{\mathrm{D}}{d}\)
\(\Rightarrow \ \frac{2}{a}=\frac{n}{d}\)
\(\Rightarrow \quad n=\frac{2 d}{a}=\frac{2 \times 2 \times 10^{-5}}{4 \times 10^{-6}}=10\)
(b) \(\frac{\lambda \mathrm{D}}{a}=n \lambda \frac{\mathrm{D}}{d}\)
\(\Rightarrow \ \frac{1}{a}=\frac{n}{d}\)
\(\Rightarrow \ n=\frac{d}{a}=\frac{2 \times 10^{-5}}{4 \times 10^{-6}}=5\)






































